2021--2022学年人教版七年级数学下册 第七章 平面直角坐标系 复习课件(共18张PPT)
文档属性
| 名称 | 2021--2022学年人教版七年级数学下册 第七章 平面直角坐标系 复习课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 202.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第7章 平面直角坐标系复习课
新人教版·数学·七年级下册
考点聚焦1
——点的坐标的符号特征
1、在平面直角坐标系中,已知点P(-2,3),点Q(-3,-1)
则点P在第____象限,点Q在第__象限。
2、在平面直角坐标系中,已知点M(a,b),且ab>0,
则点M在第 ____ 象限。
二
三
一或三
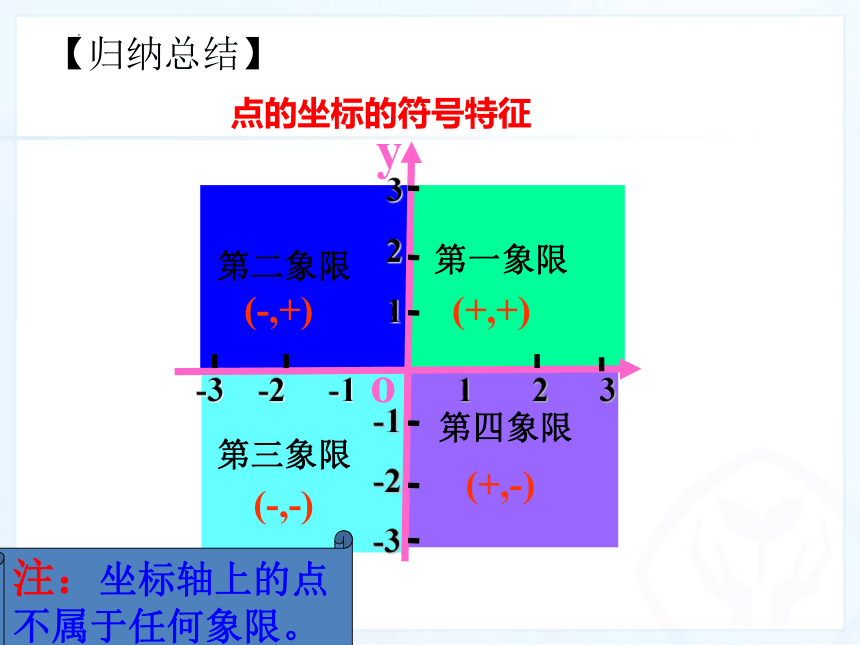
【归纳总结】
点的坐标的符号特征
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
y
o
3
2
1
-1
-2
-3
1 2 3
-3 -2 -1
注:坐标轴上的点不属于任何象限。
1、点P(0,3)在_____。
2、已知点A(x,y)满足xy=0,则点A在___________
考点聚焦2
——特殊位置点的坐标
y轴
3、若点Q(-a,2)在第一三象限角平分线上,则点Q的
坐标为________。
4、已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_____
x轴或y轴上
(2,2)
-1
3
【归纳总结】
特殊位置点的坐标特征
1、原点的坐标为 _______,x轴上的点的坐标特征:
_________ y轴上的点的坐标特征: __________
2、平面直角坐标系第一、三象限角平分线上点的坐标特征
____________ ______ , 第二、四象限角平分线上点的
坐标特征____________ ____________ 。
(0,0)
纵坐标为0
横坐标为0
横坐标和纵坐标相同
横坐标和纵坐标互为相反数
3、平行于x轴的直线上的点的_______相同,平行于y轴的
直线上点的 _________相同。
纵坐标
横坐标
考点聚焦3
——点到坐标轴的距离
1、点A(2,3)到x轴的距离为 ;点B(-4,0)
到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离
为3,且在第三象限,则C点坐标是 。
3
4
(-3,-1)
【归纳总结】
点到坐标轴的距离
1、平面直角坐标中,点p(x,y)到x轴的距离是_____ ,
到y轴的距离是_____ .
2、与x轴平行的直线上两点M1(x1,y), M2(x2,y)的距离
M1M2= , 与Y轴平行的直线上两点
N1(x,y1), N2(x,y2) 的距离 N1N2= .
|y|
|x|
|x1 - x2|
|y1 ﹣ y2|
y
A
B
C
1、已知A(1,4),B(-4,0),C(2,0).
则△ABC的面积是___.
2、将△ABC向左平移三个单位后,点A、B、C的坐标分别变为______,______,____.
3、将△ABC向下平移三个单位后,点A、B、C的坐标分别变为______,______,____.
(-2,4)
12
(-7,0)
(-1,0)
(-4,-3)
(1,1)
(2,-3)
O
(1,4)
(-4,0)
(2,0)
考点聚焦4
——用坐标表示图形的平移
【归纳总结】
用坐标表示图形的平移
平移规律:1)将点(x,y)向右(或向左)平移a个单位长度,
可得到对应点___________或___________;
2)将点(x,y)向上(或向下)平移b个单位长度,
可得到对应点___________或___________
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
例1、已知点A(x,y)在第二象限,
则点B(-x,x-y)在___。
A 第一象限 B 第二象限
C 第三象限 D 第四象限
典例探究1
点的坐标的符号特征
D
典例探究2
特殊位置点的坐标特征
例2、已知点P(m+1,m -4)在x轴负半轴,则
点p的坐标为 _____。
(-1,0)
例3、已知点A(2a+1,2+a)在第二象限的平分
线上,试求A的坐标。
解:由题意可得: 2a+1+2+a=0
a=-1
所以点A 的坐标为(-1,1)
典例探究3
点到坐标轴的距离
例4、已知AB∥x轴,A点的坐标为(3,2),并且AB=5,
求B的坐标。
解:∵ AB∥x轴,且A(3,2)
∴设点B坐标为(x,2)
又AB=5
∴|x-3|=5
∴x=8或-2
∴点B的坐标为(8,2)或(-2,2)
例5、三角形ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-3.5)。
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(1)把三角形A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标;
A
C
B
典例探究4
用坐标表示图形的平移
解:点A1(-2,2)
点B1 (-3,0)
点C1 (0,-0.5)
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(2)求出三角形 A1B1C1的面积。
D
E
分析:可把它补成一个梯形减去
两个三角形。
这节课我收获的知识是……
我学到的一种思想方法是……
我将进一步研究的问题是……
大海拾贝
本章知识结构图
确定平面内点的位置
画两条数轴
①互相垂直
②有公共原点
建立平面直角坐标系
坐标(有序数对),(x, y)
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示位置
用坐标表示平移
布置作业
1、《作业本》P28
2、 报纸
再见!
谢谢指导
第7章 平面直角坐标系复习课
新人教版·数学·七年级下册
考点聚焦1
——点的坐标的符号特征
1、在平面直角坐标系中,已知点P(-2,3),点Q(-3,-1)
则点P在第____象限,点Q在第__象限。
2、在平面直角坐标系中,已知点M(a,b),且ab>0,
则点M在第 ____ 象限。
二
三
一或三
【归纳总结】
点的坐标的符号特征
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
y
o
3
2
1
-1
-2
-3
1 2 3
-3 -2 -1
注:坐标轴上的点不属于任何象限。
1、点P(0,3)在_____。
2、已知点A(x,y)满足xy=0,则点A在___________
考点聚焦2
——特殊位置点的坐标
y轴
3、若点Q(-a,2)在第一三象限角平分线上,则点Q的
坐标为________。
4、已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_____
x轴或y轴上
(2,2)
-1
3
【归纳总结】
特殊位置点的坐标特征
1、原点的坐标为 _______,x轴上的点的坐标特征:
_________ y轴上的点的坐标特征: __________
2、平面直角坐标系第一、三象限角平分线上点的坐标特征
____________ ______ , 第二、四象限角平分线上点的
坐标特征____________ ____________ 。
(0,0)
纵坐标为0
横坐标为0
横坐标和纵坐标相同
横坐标和纵坐标互为相反数
3、平行于x轴的直线上的点的_______相同,平行于y轴的
直线上点的 _________相同。
纵坐标
横坐标
考点聚焦3
——点到坐标轴的距离
1、点A(2,3)到x轴的距离为 ;点B(-4,0)
到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离
为3,且在第三象限,则C点坐标是 。
3
4
(-3,-1)
【归纳总结】
点到坐标轴的距离
1、平面直角坐标中,点p(x,y)到x轴的距离是_____ ,
到y轴的距离是_____ .
2、与x轴平行的直线上两点M1(x1,y), M2(x2,y)的距离
M1M2= , 与Y轴平行的直线上两点
N1(x,y1), N2(x,y2) 的距离 N1N2= .
|y|
|x|
|x1 - x2|
|y1 ﹣ y2|
y
A
B
C
1、已知A(1,4),B(-4,0),C(2,0).
则△ABC的面积是___.
2、将△ABC向左平移三个单位后,点A、B、C的坐标分别变为______,______,____.
3、将△ABC向下平移三个单位后,点A、B、C的坐标分别变为______,______,____.
(-2,4)
12
(-7,0)
(-1,0)
(-4,-3)
(1,1)
(2,-3)
O
(1,4)
(-4,0)
(2,0)
考点聚焦4
——用坐标表示图形的平移
【归纳总结】
用坐标表示图形的平移
平移规律:1)将点(x,y)向右(或向左)平移a个单位长度,
可得到对应点___________或___________;
2)将点(x,y)向上(或向下)平移b个单位长度,
可得到对应点___________或___________
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
例1、已知点A(x,y)在第二象限,
则点B(-x,x-y)在___。
A 第一象限 B 第二象限
C 第三象限 D 第四象限
典例探究1
点的坐标的符号特征
D
典例探究2
特殊位置点的坐标特征
例2、已知点P(m+1,m -4)在x轴负半轴,则
点p的坐标为 _____。
(-1,0)
例3、已知点A(2a+1,2+a)在第二象限的平分
线上,试求A的坐标。
解:由题意可得: 2a+1+2+a=0
a=-1
所以点A 的坐标为(-1,1)
典例探究3
点到坐标轴的距离
例4、已知AB∥x轴,A点的坐标为(3,2),并且AB=5,
求B的坐标。
解:∵ AB∥x轴,且A(3,2)
∴设点B坐标为(x,2)
又AB=5
∴|x-3|=5
∴x=8或-2
∴点B的坐标为(8,2)或(-2,2)
例5、三角形ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-3.5)。
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(1)把三角形A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标;
A
C
B
典例探究4
用坐标表示图形的平移
解:点A1(-2,2)
点B1 (-3,0)
点C1 (0,-0.5)
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(2)求出三角形 A1B1C1的面积。
D
E
分析:可把它补成一个梯形减去
两个三角形。
这节课我收获的知识是……
我学到的一种思想方法是……
我将进一步研究的问题是……
大海拾贝
本章知识结构图
确定平面内点的位置
画两条数轴
①互相垂直
②有公共原点
建立平面直角坐标系
坐标(有序数对),(x, y)
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示位置
用坐标表示平移
布置作业
1、《作业本》P28
2、 报纸
再见!
谢谢指导
