2022--2023学年人教版 八年级数学上册 11.3.2多边形内角和 课件(共22张PPT)
文档属性
| 名称 | 2022--2023学年人教版 八年级数学上册 11.3.2多边形内角和 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 794.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
11.3.2 多边形的内角和
八年级 上册
学情分析
学习目标:
探索并证明多边形内角和和外角和公式,体会化归思想和从具体到抽象的研究问题方法.
运用多边形内角和和外角和公式解决简单问题.
学习重点:
多边形内角和和外角和公式的探索与证明过程.
欣赏一组图片,注意观察图中有哪些几何图形.
情景导入
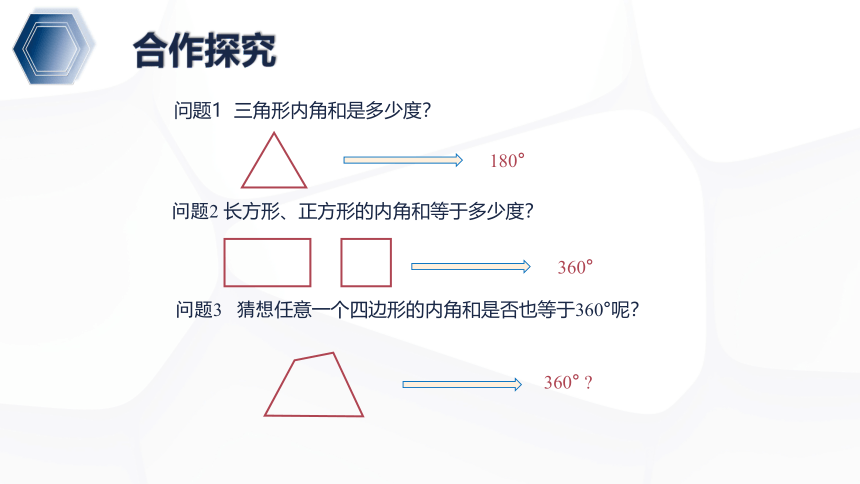
问题1 三角形内角和是多少度?
问题2 长方形、正方形的内角和等于多少度?
问题3 猜想任意一个四边形的内角和是否也等于360°呢?
合作探究
180°
360°
360°
问题4 你能利用三角形内角和定理证明你的结论吗?
小结:四边形ABCD的内角和是360°.
合作探究
A
B
C
D
方法一:分成两个三角形.
证明:如图,连接AC,将四边形分成两个三角形.
∵ 三角形内角和为180°,
∴ 四边形ABCD的内角和为180°×2=360°.
合作探究
A
B
C
D
方法二:分成四个三角形.
如图: 四边形ABCD的内角和为
180°×4-360°=360°.
方法三:分成三个三角形.
A
B
C
D
O
E
如图: 四边形ABCD的内角和为
180°×3-180°=360°.
点O也可以在
四边形外部.
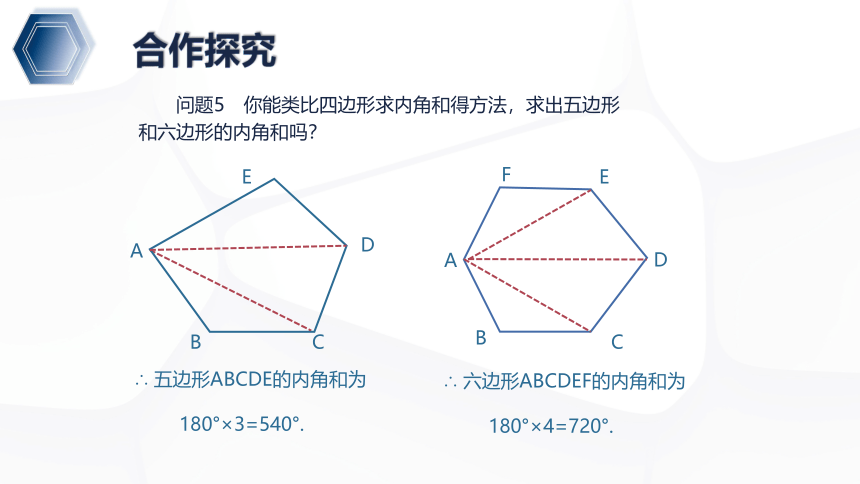
问题5 你能类比四边形求内角和得方法,求出五边形
和六边形的内角和吗?
合作探究
∴ 五边形ABCDE的内角和为
180°×3=540°.
E
F
A
B
C
D
A
B
C
D
E
∴ 六边形ABCDEF的内角和为
180°×4=720°.
合作探究
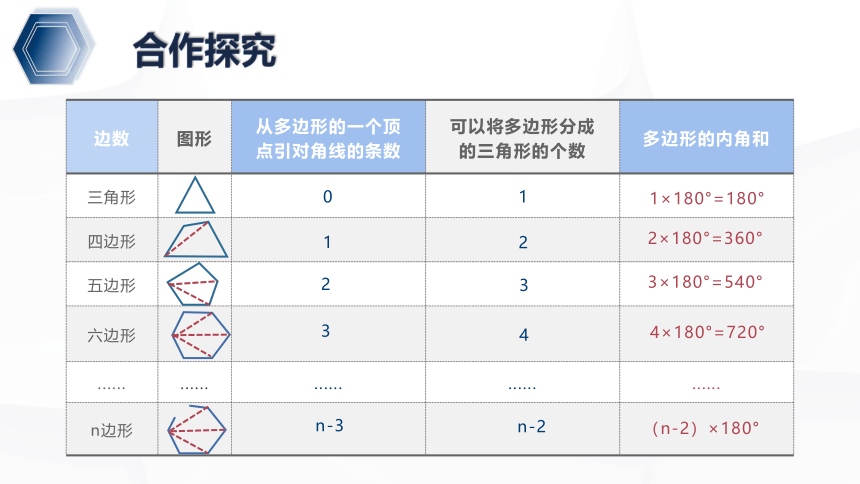
边数 图形 从多边形的一个顶点引对角线的条数 可以将多边形分成的三角形的个数 多边形的内角和
三角形
四边形
五边形
六边形
...... ...... ...... ...... ......
n边形
0
1
2
3
n-3
1
2
3
4
n-2
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
(n-2)×180°
合作探究
从n边形的一个顶点引对角线,可以引 (n-3) 条对角线,把这个n边形分成 (n-2) 个三角形, 故n边形的内角和为 180°×(n-2).
问题5 你能类比上面的求解方法,求出n边形的内角和吗?
这样就得到了多边形内角和公式:
n边形的内角和等于 (n-2)×180°.
巩固练习
解:如图,四边形ABCD 中,
∠A +∠C =180°.
∵ ∠A +∠B +∠C +∠D
=(4 - 2)×180° =360°,
∴ ∠B +∠D
=360°-(∠A + ∠C) =360°- 180° =180°.
例1 如果一个四边形的一组对角互补,那么另一
组对角有什么关系?
如果四边形的一组对角互补,那么另一组对角也互补.
D
A
B
C
巩固练习
练习1 填空
(1) 七边形的内角和是 .
(2) 已知一个多边形的内角和是720° ,则这是个 边形.
(3) 如果四边形有一个角是直角,另外三个角的度数之比是
2:3:4,那么这三个角的度数分别是 .
900°
六
60°、90°、120°
巩固练习
练习2 判断下列度数中,哪一个不可能是某个多边形内角和( )
A. 180° B. 870° C. 2700° D. 1080°
B
合作探究
问题6 小明家有一张六边形的地毯,小明绕各顶点走了一圈,
回到起点A,并面对他出发时的方向,他的身体旋转了多少度?
思考:(1)六边形的任意一个外角和它相邻
内角又怎么的数量关系?
(2)六边形所有外角加上相邻内角的总和是多少?
A
B
C
D
E
1
2
6
4
3
5
F
六边形的外角和是多少度?
合作探究
解: 如图,六边形ABCDEF 中,
∠1 +∠2 +∠3 +∠4 +∠5 +∠6
=6×180° -(6-2)×180°
=360°
问题6 小明家有一张六边形的地毯,小明绕各顶点走了一圈,
回到起点A,并面对他出发时的方向,他的身体旋转了多少度?
思考:任意多边形的外角和是多少度?
A
B
C
D
E
1
2
6
4
3
5
F
n边形的外角和等于n个平角减去n边形的内角和,与边数无关.
即:n×180° -(n-2)×180°=360°
结论: 多边形的外角等于360°.
合作探究
回顾问题6,你也可以这样理解这个结论。在行程中转过的各个角的和,就是多边形的外角和.由于走了一周,所转过的各个角的和等于一个周角,所以多边形外角和等于360°.
问题7 你知道正n边形的每个内角是多少度?那么外角呢?
正多边形的每个内角都相等,等于 .
合作探究
正多边形的每个外角都相等,等于 .
(n-2)×180°
n
360°
n
计算正多边形的内外角度数
时,先算谁更快? .
巩固练习
练习1 填空
(1) 正十边形每个内角的度数是 .
(2) 已知一个正多边形的内角是150° ,则这是个正 边形.
(3)一个正多边形的每个外角都是18°,这个正多边形的边 是 .
144°
十二
20
巩固练习
练习2 已知一个多边形,它的内角和等于外角和的3倍,求这个多边形的边数.
解: 设这个多边形的边数为n.
则(n-2)×180°=3× 360 ,
解得 n=6.
∴这个多边形的为六边形.
巩固练习
练习3 如图所示,小华在操场上点A出发,沿直线前进10米后左转40°,再沿直线前进10米,又向左转40°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
40°
40°
40°
90
巩固练习
练习4 一个多边形除一个内角外,其余各角的度数的和为2030°,求这个多边形的边数。
解: 设这个多边形的边数为n,除去的角的度数为α ,
则 α = (n-2)×180°-2030 ,
∵0<α<180,
∴ 0<(n-2)×180-2030<180,
解得 11∴n=12,因此这个多边形的边数为12.
3
11
3
11
课堂小结
谈谈本节课你的收获.
作业布置
1. 习题11.3第2、5、6题.
2. 选做题:习题11.3第9题.
11.3.2 多边形的内角和
八年级 上册
学情分析
学习目标:
探索并证明多边形内角和和外角和公式,体会化归思想和从具体到抽象的研究问题方法.
运用多边形内角和和外角和公式解决简单问题.
学习重点:
多边形内角和和外角和公式的探索与证明过程.
欣赏一组图片,注意观察图中有哪些几何图形.
情景导入
问题1 三角形内角和是多少度?
问题2 长方形、正方形的内角和等于多少度?
问题3 猜想任意一个四边形的内角和是否也等于360°呢?
合作探究
180°
360°
360°
问题4 你能利用三角形内角和定理证明你的结论吗?
小结:四边形ABCD的内角和是360°.
合作探究
A
B
C
D
方法一:分成两个三角形.
证明:如图,连接AC,将四边形分成两个三角形.
∵ 三角形内角和为180°,
∴ 四边形ABCD的内角和为180°×2=360°.
合作探究
A
B
C
D
方法二:分成四个三角形.
如图: 四边形ABCD的内角和为
180°×4-360°=360°.
方法三:分成三个三角形.
A
B
C
D
O
E
如图: 四边形ABCD的内角和为
180°×3-180°=360°.
点O也可以在
四边形外部.
问题5 你能类比四边形求内角和得方法,求出五边形
和六边形的内角和吗?
合作探究
∴ 五边形ABCDE的内角和为
180°×3=540°.
E
F
A
B
C
D
A
B
C
D
E
∴ 六边形ABCDEF的内角和为
180°×4=720°.
合作探究
边数 图形 从多边形的一个顶点引对角线的条数 可以将多边形分成的三角形的个数 多边形的内角和
三角形
四边形
五边形
六边形
...... ...... ...... ...... ......
n边形
0
1
2
3
n-3
1
2
3
4
n-2
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
(n-2)×180°
合作探究
从n边形的一个顶点引对角线,可以引 (n-3) 条对角线,把这个n边形分成 (n-2) 个三角形, 故n边形的内角和为 180°×(n-2).
问题5 你能类比上面的求解方法,求出n边形的内角和吗?
这样就得到了多边形内角和公式:
n边形的内角和等于 (n-2)×180°.
巩固练习
解:如图,四边形ABCD 中,
∠A +∠C =180°.
∵ ∠A +∠B +∠C +∠D
=(4 - 2)×180° =360°,
∴ ∠B +∠D
=360°-(∠A + ∠C) =360°- 180° =180°.
例1 如果一个四边形的一组对角互补,那么另一
组对角有什么关系?
如果四边形的一组对角互补,那么另一组对角也互补.
D
A
B
C
巩固练习
练习1 填空
(1) 七边形的内角和是 .
(2) 已知一个多边形的内角和是720° ,则这是个 边形.
(3) 如果四边形有一个角是直角,另外三个角的度数之比是
2:3:4,那么这三个角的度数分别是 .
900°
六
60°、90°、120°
巩固练习
练习2 判断下列度数中,哪一个不可能是某个多边形内角和( )
A. 180° B. 870° C. 2700° D. 1080°
B
合作探究
问题6 小明家有一张六边形的地毯,小明绕各顶点走了一圈,
回到起点A,并面对他出发时的方向,他的身体旋转了多少度?
思考:(1)六边形的任意一个外角和它相邻
内角又怎么的数量关系?
(2)六边形所有外角加上相邻内角的总和是多少?
A
B
C
D
E
1
2
6
4
3
5
F
六边形的外角和是多少度?
合作探究
解: 如图,六边形ABCDEF 中,
∠1 +∠2 +∠3 +∠4 +∠5 +∠6
=6×180° -(6-2)×180°
=360°
问题6 小明家有一张六边形的地毯,小明绕各顶点走了一圈,
回到起点A,并面对他出发时的方向,他的身体旋转了多少度?
思考:任意多边形的外角和是多少度?
A
B
C
D
E
1
2
6
4
3
5
F
n边形的外角和等于n个平角减去n边形的内角和,与边数无关.
即:n×180° -(n-2)×180°=360°
结论: 多边形的外角等于360°.
合作探究
回顾问题6,你也可以这样理解这个结论。在行程中转过的各个角的和,就是多边形的外角和.由于走了一周,所转过的各个角的和等于一个周角,所以多边形外角和等于360°.
问题7 你知道正n边形的每个内角是多少度?那么外角呢?
正多边形的每个内角都相等,等于 .
合作探究
正多边形的每个外角都相等,等于 .
(n-2)×180°
n
360°
n
计算正多边形的内外角度数
时,先算谁更快? .
巩固练习
练习1 填空
(1) 正十边形每个内角的度数是 .
(2) 已知一个正多边形的内角是150° ,则这是个正 边形.
(3)一个正多边形的每个外角都是18°,这个正多边形的边 是 .
144°
十二
20
巩固练习
练习2 已知一个多边形,它的内角和等于外角和的3倍,求这个多边形的边数.
解: 设这个多边形的边数为n.
则(n-2)×180°=3× 360 ,
解得 n=6.
∴这个多边形的为六边形.
巩固练习
练习3 如图所示,小华在操场上点A出发,沿直线前进10米后左转40°,再沿直线前进10米,又向左转40°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
40°
40°
40°
90
巩固练习
练习4 一个多边形除一个内角外,其余各角的度数的和为2030°,求这个多边形的边数。
解: 设这个多边形的边数为n,除去的角的度数为α ,
则 α = (n-2)×180°-2030 ,
∵0<α<180,
∴ 0<(n-2)×180-2030<180,
解得 11
3
11
3
11
课堂小结
谈谈本节课你的收获.
作业布置
1. 习题11.3第2、5、6题.
2. 选做题:习题11.3第9题.
