【核心素养目标】24.1.3弧、弦、圆心角 学案
文档属性
| 名称 | 【核心素养目标】24.1.3弧、弦、圆心角 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.1.3弧、弦、圆心角导学案
课题 24.1.3弧、弦、圆心角 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 通过复习旋转的知识,产生圆心角的概念,然后用圆心角和旋转的知识探索在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等,最后应用它解决一些具体问题,进一步理解和体会研究几何图形的各种方法.
核心素养分析 培养合情推理能力,发展逻辑思维能力和推理论证的表达能力,同时渗透事物之间是可相互转化的辨证唯物主义教育。感受类比思想,类比中全面透彻地理解和掌握关系定理和它的推论.
学习目标 1.理解圆心角的概念,圆的中心对称性和旋转不变性.2.理解并掌握圆心角、弧、弦之间关系定理并利用其解决相关问题.3.理解圆心角、弧、弦之间关系定理的前提条件.
重点 探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
难点 理解“在同圆或等圆”条件的意义.
教学过程
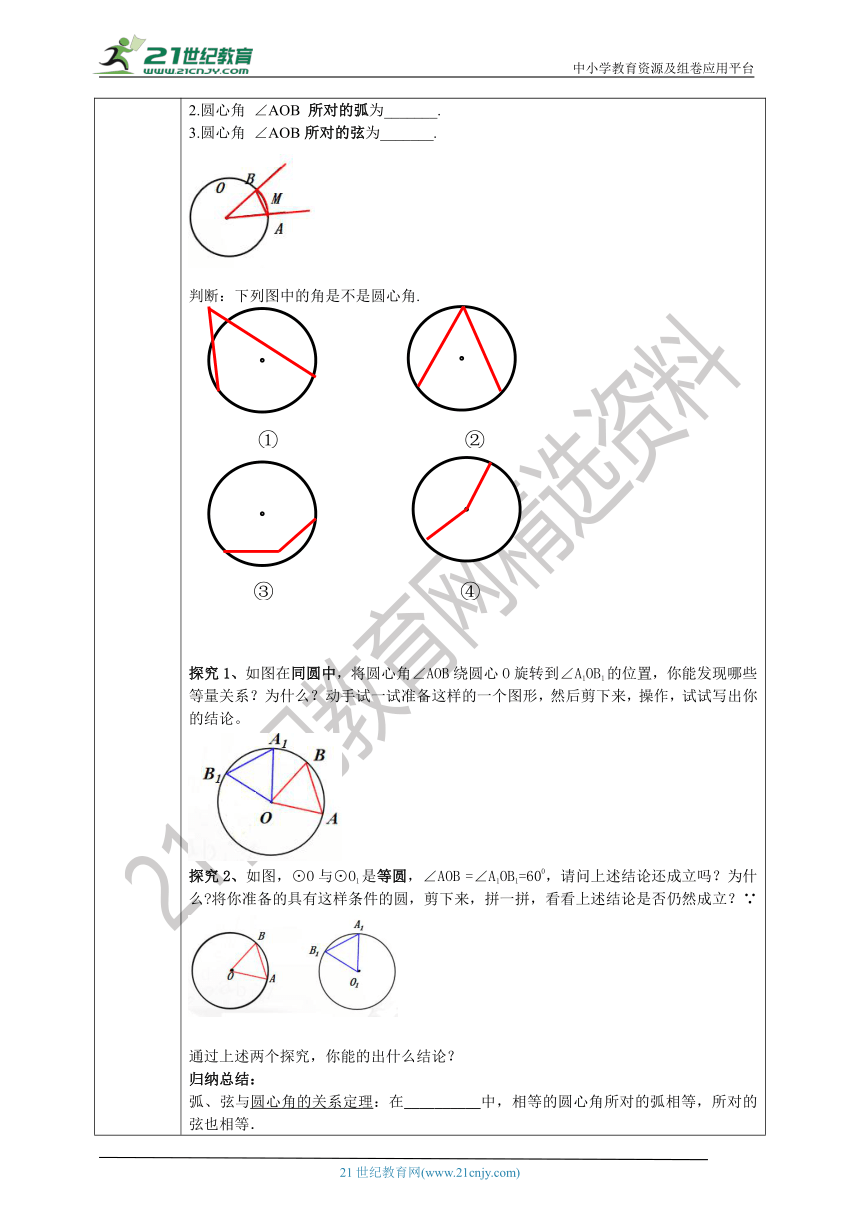
课前预学 【引入思考】 环节一:探究圆的轴对称性探究:剪一个圆形纸片,将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?重合利用这种性质,我们可以探究圆的更多性质,下面我们一起来探究:把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.观察旋转后的点N’的位置,你能得出什么结论?环节二:探究圆心角、弧、弦定理及推论我们把顶点在____的角叫做圆心角.概念总结:(如图所示)1.圆心角:顶点在圆心的角,叫圆心角,如________ .2.圆心角 ∠AOB 所对的弧为_______.3.圆心角 ∠AOB所对的弦为_______.判断:下列图中的角是不是圆心角. 探究1、如图在同圆中,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?动手试一试准备这样的一个图形,然后剪下来,操作,试试写出你的结论。探究2、如图,⊙O与⊙O1是等圆,∠AOB =∠A1OB1=600,请问上述结论还成立吗?为什么 将你准备的具有这样条件的圆,剪下来,拼一拼,看看上述结论是否仍然成立?∵ 通过上述两个探究,你能的出什么结论?归纳总结:弧、弦与圆心角的关系定理:在__________中,相等的圆心角所对的弧相等,所对的弦也相等.注意:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等”中,可否把条件“在同圆或等圆中”去掉?为什么? 从圆心角定理中,我们发现有3个量:两个圆心角相等、两条弧相等、两条弦相等类比垂径定理的学习, 这三组关系分别轮换,其它关系是否成立 小组之间讨论,看看你能得出多少结论?
新知讲解 提炼概念小结:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.典例精讲 例3 如图,在⊙O中,AB=AC ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
课堂练习 巩固训练 1.如果两个圆心角相等,那么 ( )A.这两个圆心角所对的弦相等B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等D.以上说法都不对2.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )③AC=BD;④∠BOD=∠AOC.A.1个 B.2个C.3个 D.4个3.如图,AB、CD是⊙O的两条弦.(1)如果AB=CD,那么_________,__________;(2)如果 ,那么_________, __________ ;(3)如果∠AOB=∠COD,那么_________,_______;4.如图,AB是⊙O的直径,若.求证:AC∥OD.5.如图,AB为⊙O的弦,点C,D为弦AB上的两点,且OC=OD,延长OC,OD分别交⊙O于点E,F.求证:AE=BF.6、如图,在⊙O中,2∠AOB=∠COD,那么CD=2AB成立吗?成立吗?请说明理由;如不成立,那它们之间的关系又分别是什么?答案引入思考环节一:结论:圆是旋转对称图形,具有旋转不变性环节二:我们把顶点在圆心的角叫做圆心角.图中∠AOB为圆心角圆心角∠AOB所对的弦为AB,所对的弧为AB.判断:下列图中的角是不是圆心角. 在同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,那么它们所对应的其余各组量也相等.提炼概念 典例精讲 n-m例 例3 证明:∵AB=AC,∴ AB=AC.△ABC是等腰三角形.又∠ACB=60°,∴ △ABC是等边三角形 , AB=BC=CA.∴∠AOB=∠BOC=∠AOC.本题中弧、圆心角、弦灵活转化是解题的关键.还要注意前提条件(在同圆或等圆中). 巩固训练1.D2.D3.4.5.6.
课堂小结 通过本节课的内容,你有哪些收获?
①
②
③
④
A
B
C
D
E
O
①
②
③
④
√
×
×
×
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
24.1.3弧、弦、圆心角导学案
课题 24.1.3弧、弦、圆心角 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 通过复习旋转的知识,产生圆心角的概念,然后用圆心角和旋转的知识探索在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等,最后应用它解决一些具体问题,进一步理解和体会研究几何图形的各种方法.
核心素养分析 培养合情推理能力,发展逻辑思维能力和推理论证的表达能力,同时渗透事物之间是可相互转化的辨证唯物主义教育。感受类比思想,类比中全面透彻地理解和掌握关系定理和它的推论.
学习目标 1.理解圆心角的概念,圆的中心对称性和旋转不变性.2.理解并掌握圆心角、弧、弦之间关系定理并利用其解决相关问题.3.理解圆心角、弧、弦之间关系定理的前提条件.
重点 探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
难点 理解“在同圆或等圆”条件的意义.
教学过程
课前预学 【引入思考】 环节一:探究圆的轴对称性探究:剪一个圆形纸片,将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?重合利用这种性质,我们可以探究圆的更多性质,下面我们一起来探究:把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.观察旋转后的点N’的位置,你能得出什么结论?环节二:探究圆心角、弧、弦定理及推论我们把顶点在____的角叫做圆心角.概念总结:(如图所示)1.圆心角:顶点在圆心的角,叫圆心角,如________ .2.圆心角 ∠AOB 所对的弧为_______.3.圆心角 ∠AOB所对的弦为_______.判断:下列图中的角是不是圆心角. 探究1、如图在同圆中,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?动手试一试准备这样的一个图形,然后剪下来,操作,试试写出你的结论。探究2、如图,⊙O与⊙O1是等圆,∠AOB =∠A1OB1=600,请问上述结论还成立吗?为什么 将你准备的具有这样条件的圆,剪下来,拼一拼,看看上述结论是否仍然成立?∵ 通过上述两个探究,你能的出什么结论?归纳总结:弧、弦与圆心角的关系定理:在__________中,相等的圆心角所对的弧相等,所对的弦也相等.注意:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等”中,可否把条件“在同圆或等圆中”去掉?为什么? 从圆心角定理中,我们发现有3个量:两个圆心角相等、两条弧相等、两条弦相等类比垂径定理的学习, 这三组关系分别轮换,其它关系是否成立 小组之间讨论,看看你能得出多少结论?
新知讲解 提炼概念小结:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.典例精讲 例3 如图,在⊙O中,AB=AC ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
课堂练习 巩固训练 1.如果两个圆心角相等,那么 ( )A.这两个圆心角所对的弦相等B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等D.以上说法都不对2.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )③AC=BD;④∠BOD=∠AOC.A.1个 B.2个C.3个 D.4个3.如图,AB、CD是⊙O的两条弦.(1)如果AB=CD,那么_________,__________;(2)如果 ,那么_________, __________ ;(3)如果∠AOB=∠COD,那么_________,_______;4.如图,AB是⊙O的直径,若.求证:AC∥OD.5.如图,AB为⊙O的弦,点C,D为弦AB上的两点,且OC=OD,延长OC,OD分别交⊙O于点E,F.求证:AE=BF.6、如图,在⊙O中,2∠AOB=∠COD,那么CD=2AB成立吗?成立吗?请说明理由;如不成立,那它们之间的关系又分别是什么?答案引入思考环节一:结论:圆是旋转对称图形,具有旋转不变性环节二:我们把顶点在圆心的角叫做圆心角.图中∠AOB为圆心角圆心角∠AOB所对的弦为AB,所对的弧为AB.判断:下列图中的角是不是圆心角. 在同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,那么它们所对应的其余各组量也相等.提炼概念 典例精讲 n-m例 例3 证明:∵AB=AC,∴ AB=AC.△ABC是等腰三角形.又∠ACB=60°,∴ △ABC是等边三角形 , AB=BC=CA.∴∠AOB=∠BOC=∠AOC.本题中弧、圆心角、弦灵活转化是解题的关键.还要注意前提条件(在同圆或等圆中). 巩固训练1.D2.D3.4.5.6.
课堂小结 通过本节课的内容,你有哪些收获?
①
②
③
④
A
B
C
D
E
O
①
②
③
④
√
×
×
×
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
