8.3怎样判定三角形全等

课件72张PPT。8.3 怎样判定三角形全等如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?
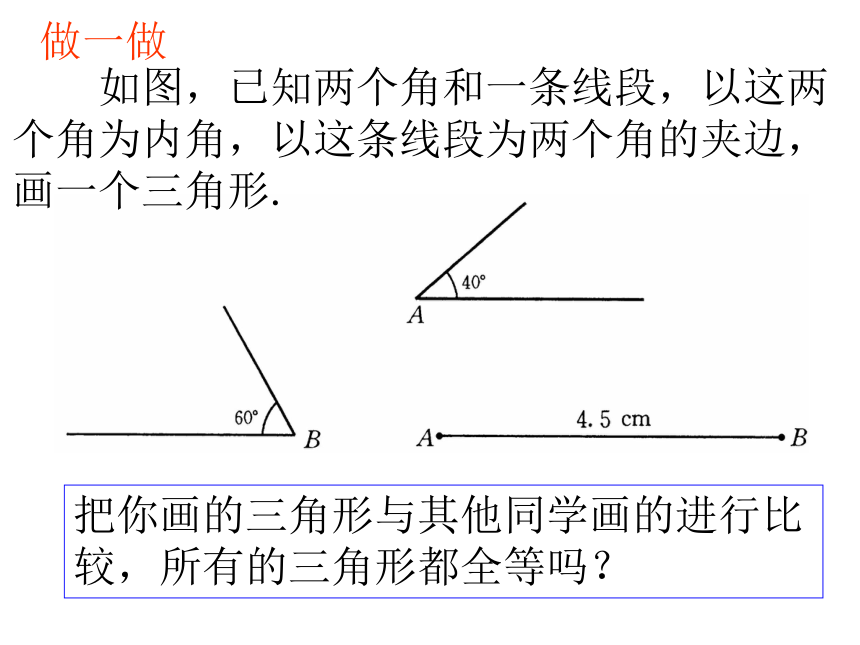
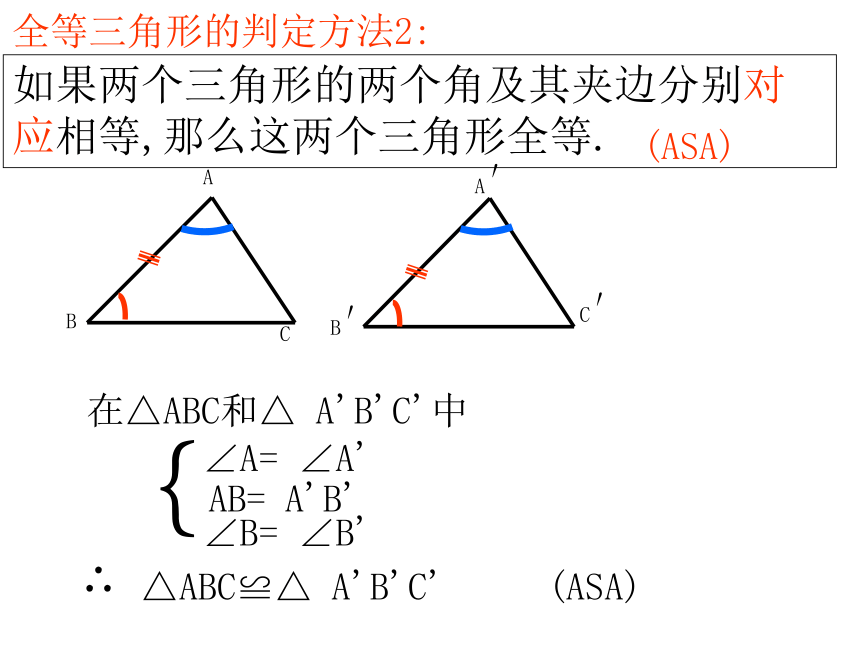
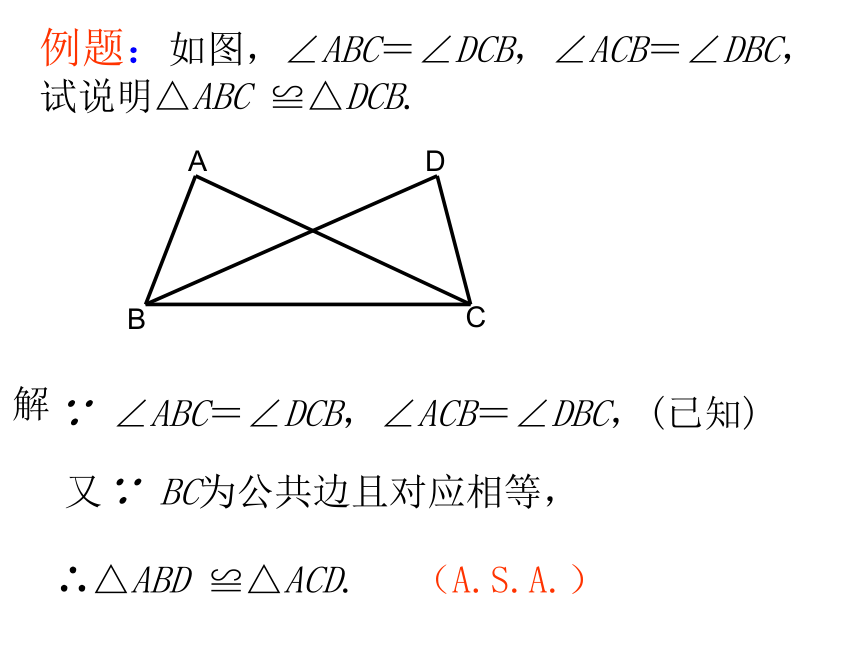
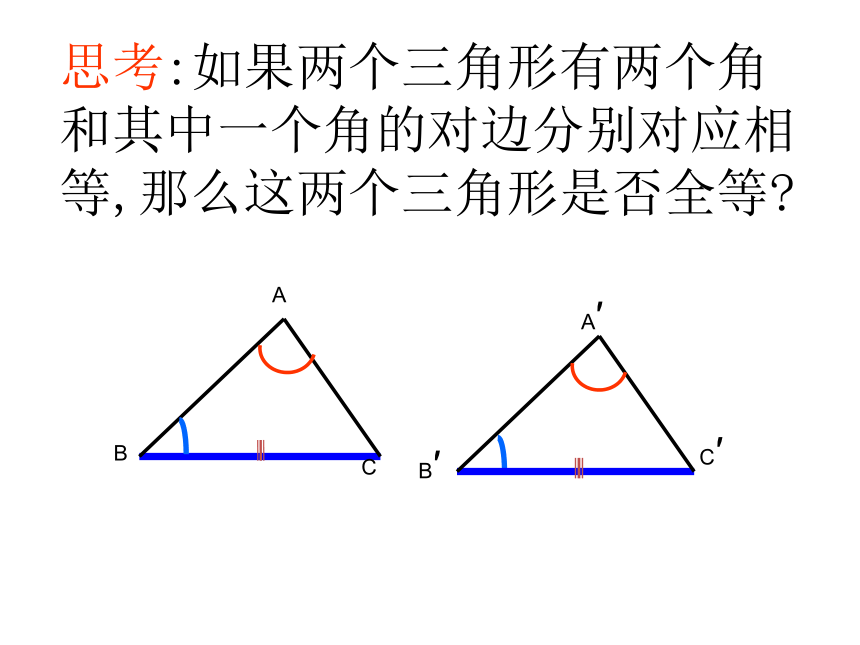
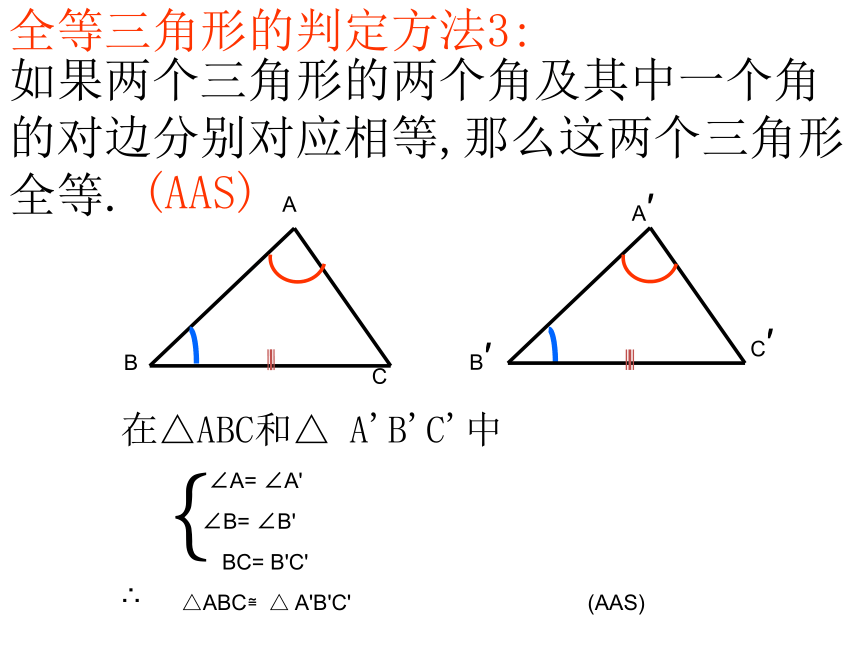
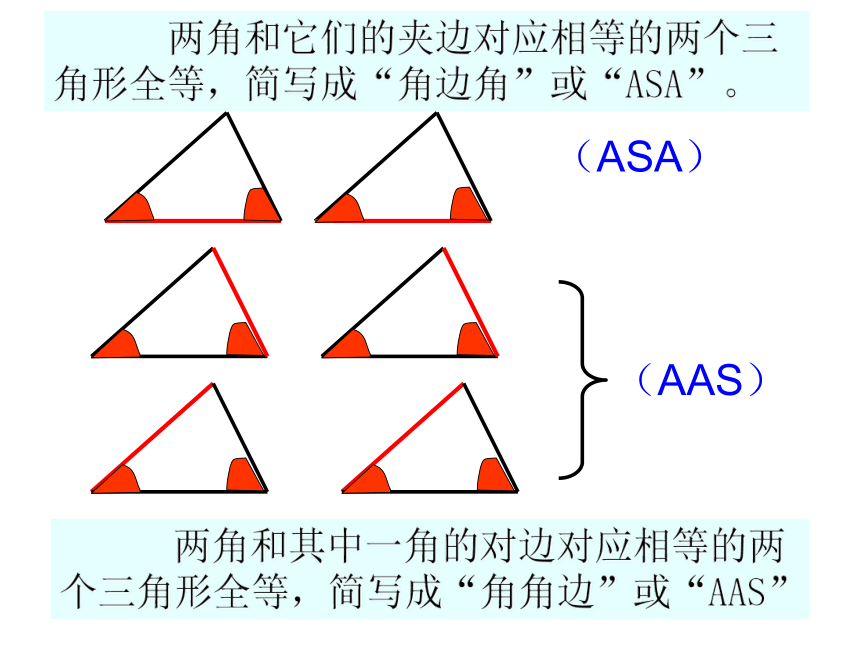
你能说明其中理由吗?议一议怎么办？可以帮帮我吗？如果知道两个三角形的两个角及一条边分别对应相等，这两个三角形一定全等吗？这时应该有两种不同的情况：（1）两个角及两角的夹边；（2）两个角及其中一角的对边问题导入　 如图，已知两个角和一条线段，以这两个角为内角，以这条线段为两个角的夹边，画一个三角形.做一做把你画的三角形与其他同学画的进行比较，所有的三角形都全等吗？全等三角形的判定方法2:如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.在△ABC和△ A'B'C'中∠A= ∠A'AB= A'B'∠B= ∠B'｛(ASA)例题：如图，∠ABC＝∠DCB，∠ACB＝∠DBC，试说明△ABC ≌△DCB.解∵ ∠ABC＝∠DCB，∠ACB＝∠DBC，(已知)又∵ BC为公共边且对应相等，∴△ABD ≌△ACD.（A.S.A.）思考:如果两个三角形有两个角和其中一个角的对边分别对应相等,那么这两个三角形是否全等?全等三角形的判定方法3:如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.在△ABC和△ A'B'C'中∠A= ∠A'BC= B'C'∠B= ∠B'｛(AAS) 两角和它们的夹边对应相等的两个三角形全等，简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等，简写成“角角边”或“AAS”（ASA）练　习
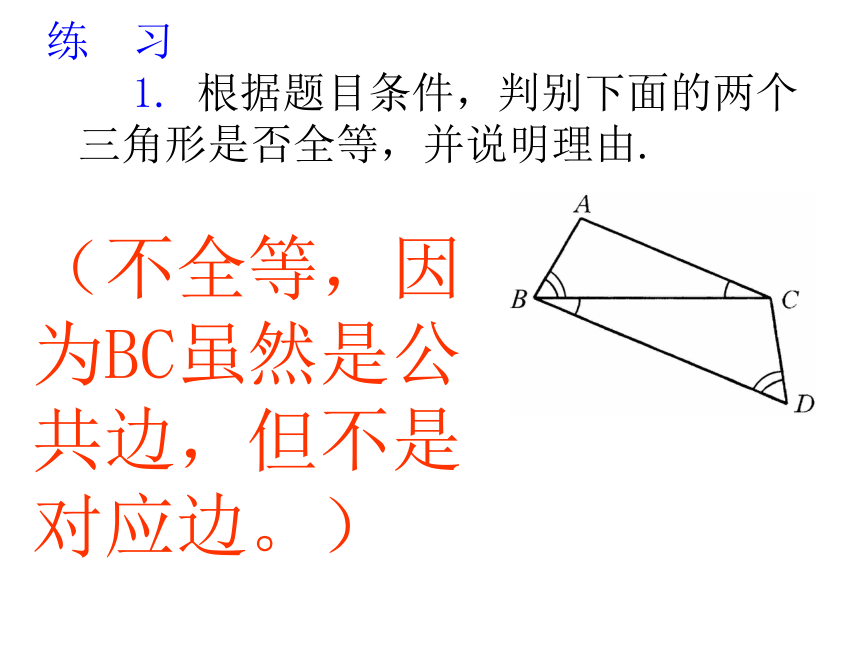
1. 根据题目条件，判别下面的两个三角形是否全等，并说明理由.
（不全等，因为BC虽然是公共边，但不是对应边。）2.要使下列各对三角形全等，需要增加什么条件？
（1）　　　　　　　（2）　　　　　　　　　3.如图，已知AB与CD 相交于O，∠A＝∠D，CO＝BO，说明△AOC与△DOB全等的理由. （利用A.A.S定理说明） 4. 已知：如图，△ABC ≌△A’B’C’，AD、A’D’ 分别是△ABC 和△A’B’C’的高。试说明AD＝ A’D’ ，并用一句话说出你的发现。思考题:全等三角形对应边上的高也相等。5、△ABC是等腰三角形，AD、BE 分别是∠A、∠B 的角平分线，△ABD和△BAE 全等吗？试说明理由.∵ △ABC是等腰三角形∴ AC=BC ∠A＝∠B 又∵ AD、BE 分别是∠A、∠B 的角平分线解∴ ∠BAD＝ ∠A
∠ABE＝ ∠B∴ ∠BAD =∠ABE∴△ABD≌△BAE (A.S.A)思考题:1、如图 ，AB=AC,∠B=∠C,那么△ABE 和△ACD全等吗？为什么？试一试（ASA）∴ △ABE ≌△ACD（已知）AB=AC∠B=∠C∠A= ∠A（公共角）∵在△ABE与△ACD中说明:答:△ABE ≌△ACD(已知)2、如图，AD=AE,∠B=∠C，那么BE和CD相等么？为什么？（全等三角形对应边相等）∴ BE=CD（AAS）∴ △ABE ≌△ACD（已知） AE=AD∠B=∠C∠A= ∠A（公共角）在△ABE与△ACD中说明:答:BE =CD(已知)小结： 本节课我们主要学习了有关全等三角形的“两角一边”识别方法，有两种情况：
1. 两个角及两角的夹边；
2.两个角及其中一角的对边。（都能够用来识别三角形全等。） 如果一个三角形的两个角及其夹边分别与另一个三角形的两个角及其夹边对应相等,那么这两个三角形全等. 简写成“角边角”或“ASA”.判定方法1：做一做：按要求画三角形，并与同伴交流.
已知：∠A=600、∠B=450、BC=3cmBCA7504503cm剪下来，与同伴进行比较，它们能否互相重合？600结论：如果一个三角形的两个角及其中一角的对边分别与另一个三角形的两个角及其中一角的对边对应相等,那么这两个三角形全等.这个判定方法可以简单地用“角角边” 或“ AAS”来表示.小结(1) 两角和它们的夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.(2) 两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.知识要点：（3）探索三角形全等是证明线段相等（对应边相等），角
相等（对应角相等）等问题的基本途径。数学思想：要学会用分类的思想，转化的思想解决问题。“角边角”以及“角角边”都是通过两个三角形的三对元素对应相等来判定三角形全等的.除此之外,在两个三角形中,三对元素对应相等的情况还有哪几种？还有三种情况：
两边一角,三条边,三个角分别对应相等.我们 前面学过的三角形全等的判定有几种？ 那么两个三角形有两条边和一个角分别对应相等又有几种情况呢？这两种情况都能判定两个三角形全等吗？6厘米6厘米4厘米4厘米3003002、剪下你画出的这些三角形，与其它同学的进行比较，这些三角形能重合吗？1、（1）已知线段a=4厘米，b=6厘米，∠α=30°。在草纸上
画出△ABC，使BC=a, AC=b, ∠C=∠α。
（2）已知线段a=4厘米，b=6厘米， ∠α=45°.在草纸上
画出△ABC，使BC=a, AC=b, ∠C=∠α。
（3）已知线段a=6厘米，b=8厘米，∠α=30°。在草纸上
画出△ABC，使BC=a, AC=b, ∠C=∠α。
请同学们分成三组来完成这三个问题。3、通过上面的实验，你能得到什么结论？与同学交流。 三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）。在△ABC和△ DEF中∴ △ABC ≌△ DEF（SSS）用符号语言表达为： 三角形全等判定方法1
三步走：①准备条件②摆齐条件③得结论注重书写格式除了SSS外,还有其他情况吗？继续探索三角形全等的条件.思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件中的三个时，有四种情况:SSS不能!?继续探讨三角形全等的条件：两边一角思考：已知一个三角形的两条边和一个角，那么这两条边
与这一个角的位置上有几种可能性呢？图一图二在图一中， ∠A是AB和AC的夹角，符合图一的条件，它可称为“两边夹角”。符合图二的条件， 通常
说成“两边和其中一边的对角”已知△ABC，画一个△A′B′C′使A B =A′B′,A C =A′ C ′, ∠A =∠A′。结论:两边及夹角对应相等的两个三角形全等？思考： ① △A′ B′ C′ 与 △ABC 全等吗？如何验正？画法: 1.画 ∠DA′ E= ∠A；2.在射线A D上截取A′ B′ =AB,在射线A′ E上截取A ′C ′=AC;3. 连接B ′C′.′ACBA′EDCB′′思考： ②这两个三角形全等是满足哪三个条件？探索边角边 三角形全等判定方法2用符号语言表达为：在△ABC与△DEF中∴△ABC≌△DEF（SAS） 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA1.在下列图中找出全等三角形练习一探索边边角两边及其中一边的对角对应相等的两个三角形全等吗?已知：AC=10cm,BC=8cm, ∠A=45 °.△ABC的形状与大小是唯一确定的吗?探索边边角SSA不存在显然： △ABC与△AB’C不全等ABDABCSSA不能判定全等两边及一角对应相等的两个三角形全等吗？①两边及夹角对应相等的两个三角形全等（SAS)；②两边及其中一边的的对角对应相等的两个三角形不一定全等．③ 现在你知道哪些三角形全等的判定方法？SSS,　SAS例. 如图，AC=BD，∠CAB= ∠DBA，你能判断BC=AD吗？说明理由。证明:在△ABC与△BAD中 AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△BAD（SAS）(已知)(已知)(公共边)∴BC=AD (全等三角形的对应边相等） 因为全等三角形的对应角相等，对应边相等，所以，证明分别属于两个三角形的线段相等或角相等的问题，常常通过证明两个三角形全等来解决。归纳C在下列推理中填写需要补充
的条件，使结论成立：
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC（ ）∠ AOB∠ DOC对顶角相等SAS练习一(2).如图，在△AEC和△ADB中，已知AE=AD，AC=AB，请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB（ ）AEADACABSAS解：在△AEC和△ADB中1.若AB=AC，则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSA S练习二AD=ADBD=CDS2.如图，要证△ACB≌ △ADB ，至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CAB= ∠ DABAC=ADSBC=BD3.如图:己知AD∥BC,AE=CF,AD=BC,E、Ｆ都在直线ＡＣ上，试说明ＤＥ∥ＢＦ。●●练习三●●例.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF，
还需增加一个什么条件？同步练习 三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）。在△ABC和△ DEF中∴ △ABC ≌△ DEF（SSS）用符号语言表达为： 三角形全等判定方法1 三角形全等判定方法2用符号语言表达为：在△ABC与△DEF中∴△ABC≌△DEF（SAS） 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBAABDABCSSA不能判定全等用符号语言表达为：在△ABC与△ A′B′C′中:∴△ABC≌△ A′B′C′（SAS）判定方法2 如果一个三角形的两条边及其夹角分别与另一个三角形的两条边及其夹角对应相等，那么这两个三角形全等。这个判定方法可以简单地用“边角边”或“SAS”来表示。归纳如图，下列三角形中，哪两个三角形是全等三角形？ ＤＥＦＡＢＣ①解：这个方案是对的。例2 如图，为测量池塘边上A，B两点之间的距离，小亮设计了这样一个方案 ：在平地上取一个能直接到达A和B的点C，然后在射线AC上取一点D，使CD=CA，在射线BC上取一点E，使CE=CB。连接DE，那么线段DE的长就等于A,B两点之间的距离。你认为他的方案对吗？为什么?(2)剪下画出的三角形，与其他同学剪得的三角形比较。这些三
角形是否一定能重合？（1）如下图，已知线段a,b, ∠β。在草纸上画出△ABC，
使AB=b，AC=a，∠B= ∠β。abβ图8-11（3）如果一个三角形的两边及其中一边的对角与另一个三角形的两边及其中一边的对角分别对应相等，能判定这两个三角形全等吗？ 如图8-11，AC=A′C′,AB=A′B′,∠B=∠B′,△ABC与△A′B′C′不能重合，显然它们不全等。因此，在这种那个情况下，不能判定这两个三角形全等。
以下三角形全等吗？
1、AB=3 BC=4 ∠B=60°
DE=3 EF=4 ∠F=30°
2、 AB=3 BC=4 ∠E=60°
AB=3 BC=4 ∠F=60°
3、 AB=3 BC=4 ∠C=30°
DE=3 EF=4 ∠F=30°想一想练习
1、如图，已知BC=BD, ∠ABC=∠ABD, △ABC和△ABD全等吗？
为什么？
2、如图，已知AB=AD，AC=AE，△ABE和△ADC全等吗？为什么？(第1题)(第2题）判定方法2 如果一个三角形的两条边及其夹角分别与另一个
三角形的两条边及其夹角对应相等，那么这两个三角形全等。这个判定方法可以简单地用”边角边“或”SAS”来表示通过这节课的学习你有什么收获?5、如图，如果∠ABC=∠DBC，AC=DB，那么△ABC与△DCB是
否全等？为什么？6、如图，AC=DF,AC∥DF，BE=CF。
（1）BC与EF相等吗？
（2）△ABC与△DEF是否全等？选做题
课本35页4题 判定三角形全等的方法：“角边角”、“角角边”及“边角边”.如果一个三角形的三条边分别与另一个三角形的三条边对应相等,那么这两个三角形是否全等?abc用符号语言表达为：在△ABC与△ A′B′C′中: ∵AB=A′B′,AC=A′C′,BC= B′C′∴△ABC≌△ A′B′C′（SSS）三个角分别对应相等的两个三角形是否全等？ 判定两个三角形全等,至少要有一条边对应相等.通过这节课的学习你有什么收获? -- 青岛版Thank You !