第九章 解直角三角形（共5节）

课件98张PPT。第9章 解直角三角形
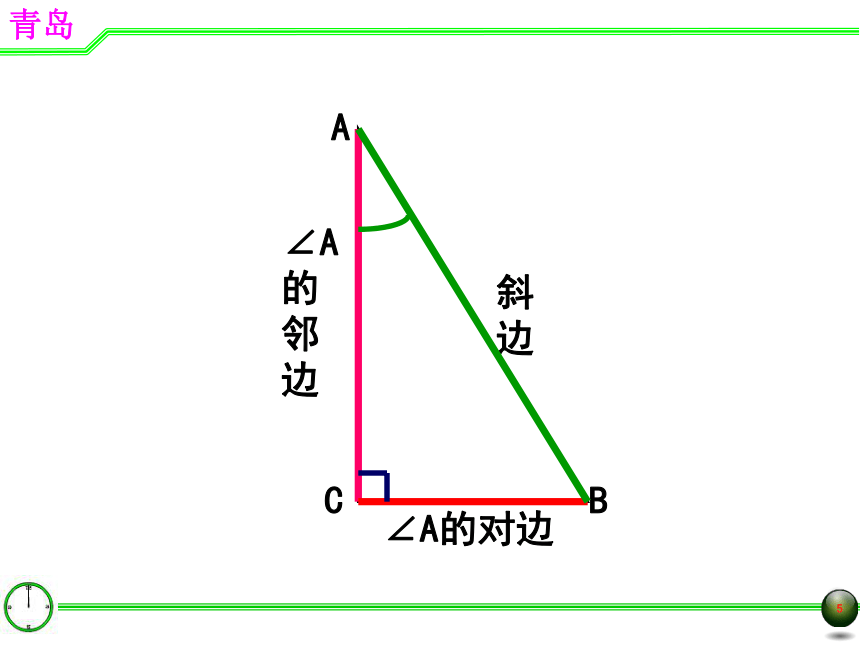
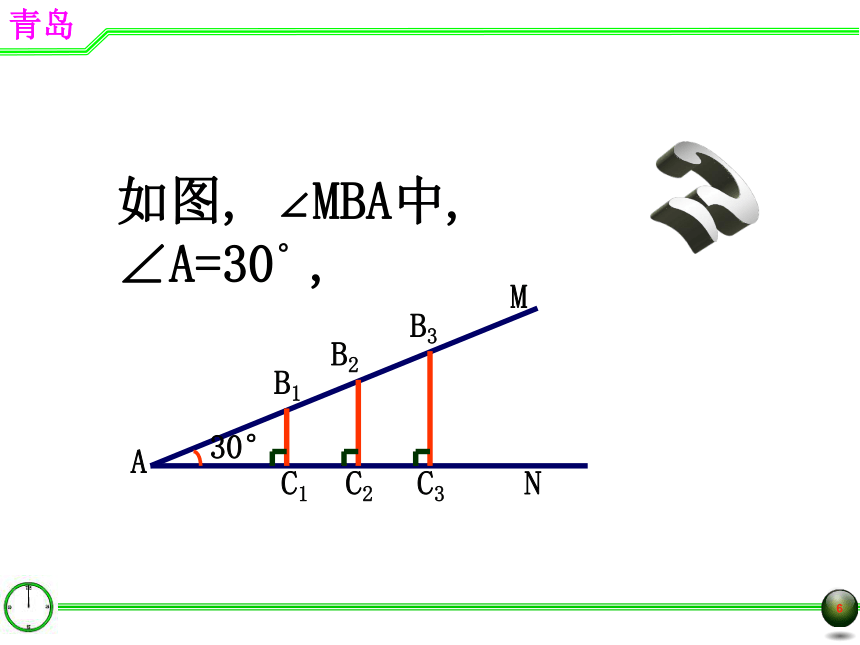
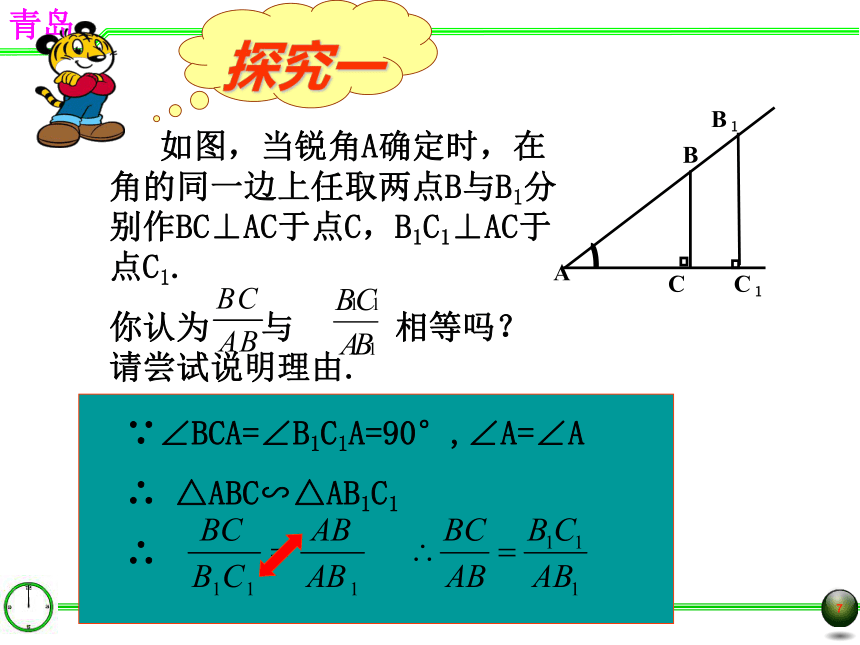
（共5节） -- 青岛版9.1 锐角三角比??∠A的对边∠A的邻边CAB斜边C1AMN？30°如图, ∠MBA中, ∠A=30°, 如图，当锐角A确定时，在角的同一边上任取两点B与B1分别作BC⊥AC于点C，B1C1⊥AC于点C1.
你认为　 与　　　相等吗？请尝试说明理由.探究一交流新知一1.sin∠A通常省略“∠”写成sinA的形式
2.sinA 不是一个角，是一个比值，没有单位
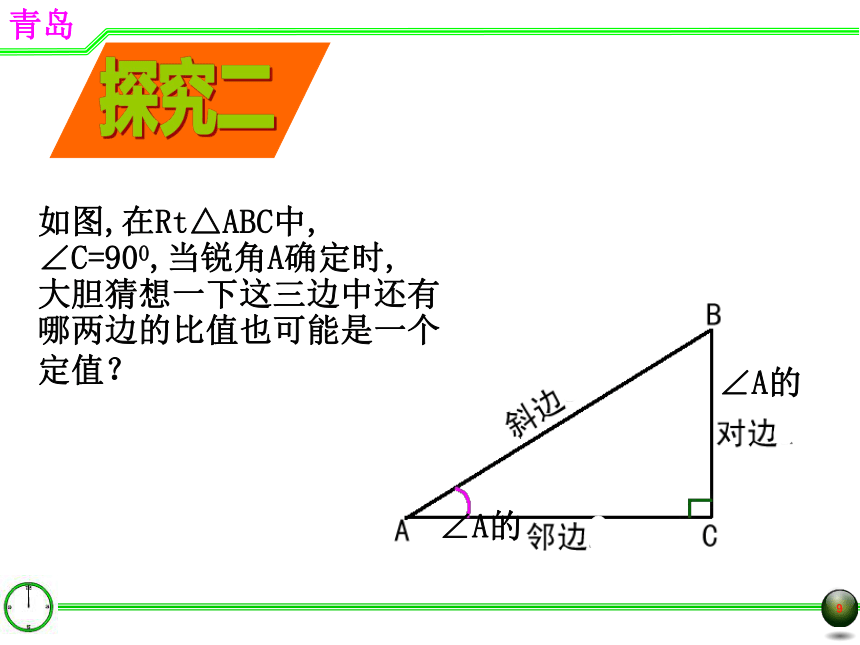
3.sinA不是 sin与A的乘积 ★sin∠BAC,sin∠1 、sin56°探究二如图,在Rt△ABC中, ∠C=900,当锐角A确定时, 大胆猜想一下这三边中还有哪两边的比值也可能是一个定值？
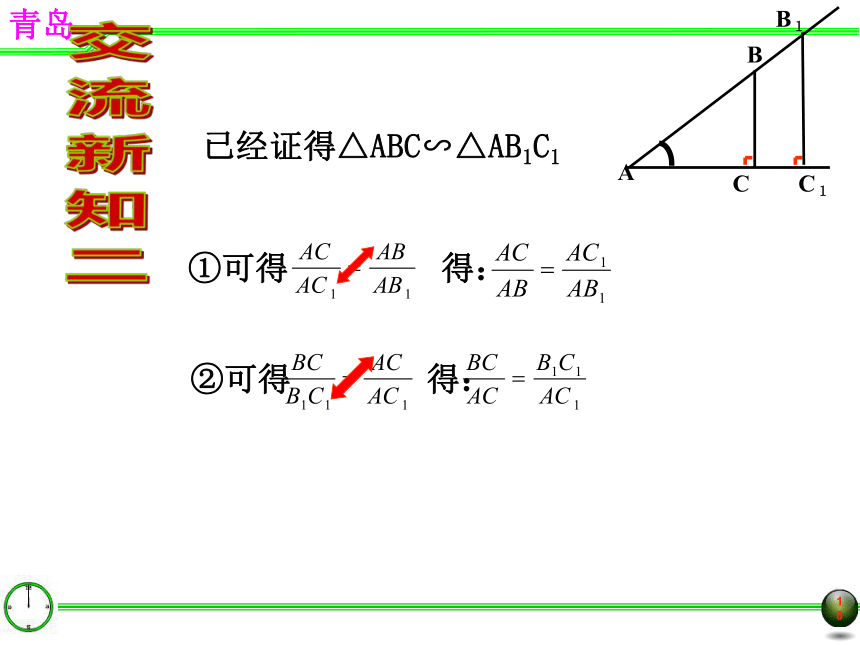
∠A的∠A的已经证得△ABC∽△AB1C1
交
流
新
知
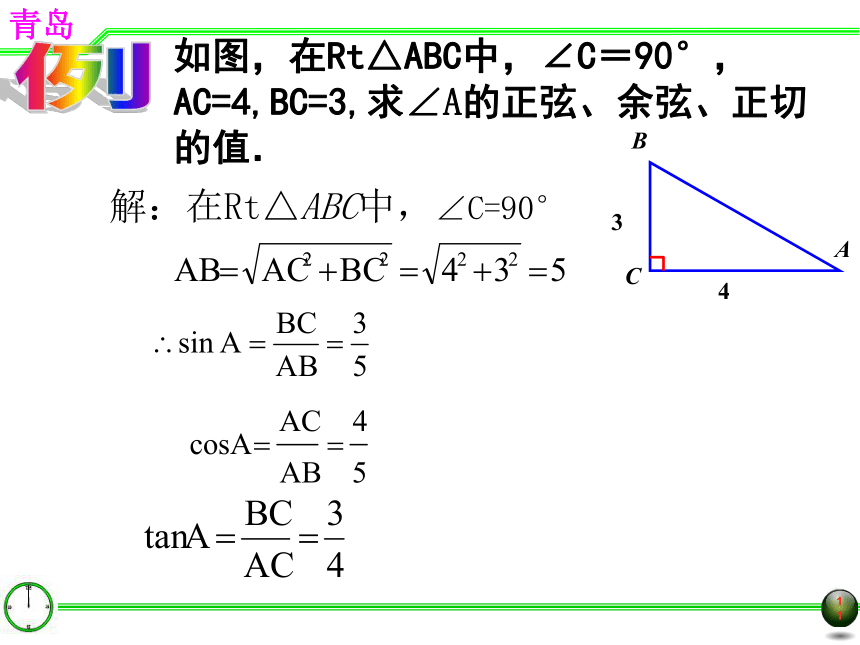
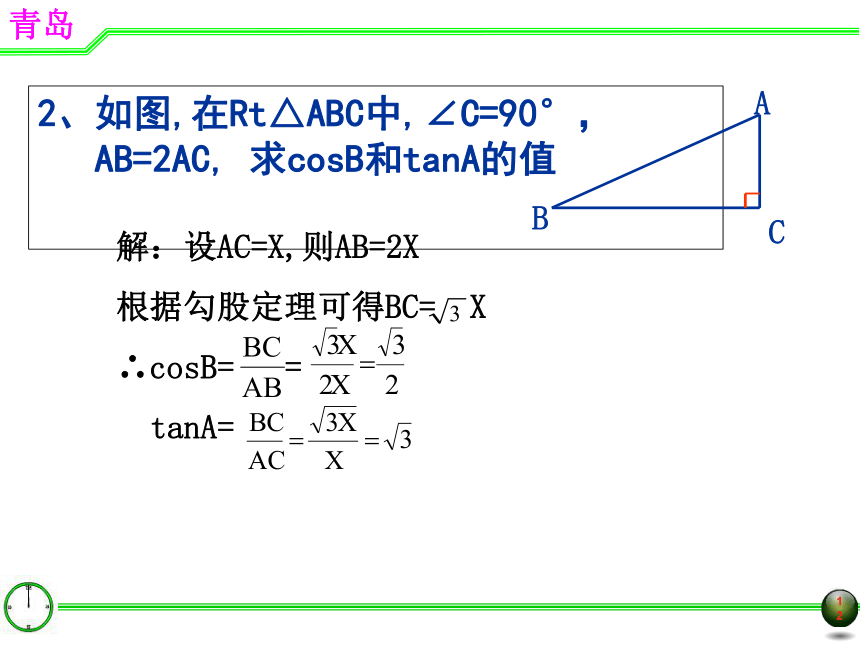
二如图，在Rt△ABC中，∠C＝90°，AC=4,BC=3,求∠A的正弦、余弦、正切的值．例解：在Rt△ABC中，∠C=90°42、如图,在Rt△ABC中,∠C=90°，AB=2AC, 求cosB和tanA的值解：设AC=X,则AB=2X
根据勾股定理可得BC= X
∴cosB= =
tanA=
练习提升
1、如图,在Rt△ABC中,∠C=90°，根据下列条件填空
（1）BC= ， AB=1，sinA= tanB=
（2）a=6， sinA=

c= sinB=
CABab10cA锐角A的三角比随着角的大小的变化而变化BCB1C1B2C2sin ∠BAC=
sin ∠B1AC1=
sin ∠B2AC2=
学习了一个重要概念：锐角三角函数小结梳理：我们学习了－－－－三角形在正方形网格纸中的位置如图所示，则sinα的值是﹙ ﹚
A． B． C． D．c能力提升 （1）如图：正方形网格中，∠A如图放置，则tanA= . 212 求网格中的锐角三角比，构造顶点在格点上的直角三角形。能力提升12相交所成的锐角为α，则sinα= . 435 将抽象问题直观展现，只看长度，构造直角三角形，求锐角三角比。能力提升（3）在Rt△ABC中，∠ABC=90°，BD⊥AC于D，AB=2，BC=3，求tan∠DBC的值.解：∵ ∠ABC=90°，BD⊥AC于D∴ ∠DBC + ∠DBA=90°
∠A+ ∠DBA =90 °∴ ∠DBC = ∠A∵在Rt△ABC中，∠ABC=90° ，AB=2，BC=323 相等的角的锐角三角比也相同，可以互相转化。拓展延伸在Rt△ABC中,∠C=900 ,AC=4,
求AB、BC的值解：
∵∴ 设BC=3k，则AB=5k，根据勾股定理可得AC=4k
∵ AC=4k=4∴ k=1∴ AB=5，BC=3判断对错:1) 如图 (1) tanA=

(2) cosA=

(3) sinA=
(4) tanA= m
2)如图，锐角△ABC中，tanA=火眼金睛1.判断对错:1) 如图 (1) sinA= （ ）

(2)tanB= （ ）

(3)cosB=0.6m （ ）
(4)SinB=0.8 （ ）
√√××cosB是一个比值（注意比的顺序），无单位；2)如图，sinA= （ ） ×考考你1.判断对错:ABC如图 (1)sinA= （ ）

(2)sinB= （ ）
(3)tanA= （ ）


当堂检测2、如图，在Rt△ABC中，∠C＝90°，AB=13，BC=5 ,求∠A的正弦、余弦、正切的值．解：在Rt△ABC中，C=90°考考你3 -- 青岛版Thank You !9.2 30°45°60°角的三角函数值复习:在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边比、对边与邻边的比也随之确定,分别叫做∠A的正弦、余弦、正切.ABCcbasinA＝ , cosA＝ , tanA＝┌sinA=cosB问题:如图,在Rt△ABC中,∠C＝90°,AC＝a,∠A＝30°,求BC.
ABC分析:
1.由∠C＝90°,∠A＝30°,我们想到了什么?
2.假设BC＝x,那么AB等于多少?
3.接下来如何求出BC?┌30°ax2xAC2＋BC2＝AB2即a2＋x2＝(2x)2解得x＝
问题:如图,在Rt△ABC中,∠C＝90°,AC＝a,
∠A＝30°,求BC.BAC┌2xax30°
本题除了这种解法外还有其它的解法吗?解:由∠C＝90°,∠A＝30°得AB＝2BC,设BC＝x则AB＝2x,由勾股定理得观察一副三角尺,其中有几个锐角?它们分别等于多少度?
⑴sin30°等于多少?你是怎样得到的?与同伴进行交流.
⑵cos30°等于多少?tan30°呢?新课 sin30°＝cos30°＝tan30°＝30°60°ABCa2a＝＝＝＝＝＝如下图所示,假设BC＝a,则
AB＝ ,AC＝2a┌做一做⑴60°角的三角函数值分别是多少?你是怎样得到的?
⑵45°角的三角函数值分别是多少?你市怎样得到的?
⑶完成下表:sin60° ＝cos60° ＝tan60° ＝sin45° ＝cos45° ＝tan45° ＝＝＝＝＝＝＝＝＝＝＝＝＝1ABCa2a60°30°┌ABC45°45°┌aa1想一想:如果已知某一锐角的某种三角函数值,你能求出这一锐角吗?比如tanA＝1,锐角A是多少度?例1 计算:
(1)sin300+cos450;(2) sin2600+cos2600-tan450.提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.解: (1)sin300+cos450(2) sin2600+cos2600-tan450例２　一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差（结果精确到0.01m）.OBDAC解:如图,根据题意可知,∠AOD＝ ×60°＝30°,OD＝2.5m, ∴OC＝ODCOS30°＝2.5×≈2.165（m） ∴AC＝2.5－2.165 ≈0.34 （m）
所以,最高位置与最低位置的高度差约 为0.34m.随堂练习⒈计算:
⑴ sin60°－tan45°;
⑵ cos60°＋tan60°;
⑶ sin45°＋sin60°－2cos45° ⒉某商场有一自动扶梯,其倾斜角为30°,高为7m.扶梯的长度是多少?回顾与思考 本节课你学到了什么新知识，说说你的表现如何？
（好，一般，有待提高） -- 青岛版Thank You !9.3 用计算器求锐角三角比温故知新特殊角的三角函数．1例题讲解例题讲解0.96590.81211.59260.96860.80710.50120.99993.10220.01750.99990.17360.98480.34200.93970.50.86600.64280.76600.70710.70710.76600.64280.86600.50.34200.93970.17360.98480.01750.9999 当锐角α逐渐增大时，它的正弦值逐渐增大，它的余弦值逐渐减小. 当0°<α<90°时，0选做题:课本P73 B组 1题 -- 青岛版Thank You !9.4 解直角三角形复习30°、45°、60°角的正弦值、余弦值和正切值如下表：对于sinα与tanα，角度越大，函数值也越大；（带正）
对于cosα，角度越大，函数值越小。问题： 要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角a一般要满足50°≤a≤75°.现有一个长6m的梯子，问：
（1）使用这个梯子最高可以安全攀上多高的墙（精确到0.1m）？
（2）当梯子底端距离墙面2.4m时，梯子与地面所成的角a等于多少（精确到1°）？这时人是否能够安全使用这个梯子？这样的问题怎么解决问题（1）可以归结为：在Rt △ABC中，已知∠A＝75°，斜边AB＝6，求∠A的对边BC的长． 问题（1）当梯子与地面所成的角a为75°时，梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度．因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m所以 BC≈6×0.97≈5.8由计算器求得 sin75°≈0.97由 得对于问题（2），当梯子底端距离墙面2.4m时，求梯子与地面所成的角a的问题，可以归结为：在Rt△ABC中，已知AC＝2.4，斜边AB＝6，求锐角a的度数由于利用计算器求得a≈66° 因此当梯子底墙距离墙面2.4m时，梯子与地面
所成的角大约是66°由50°＜66°＜75°可知，这时使用这个梯子是安全的．在图中的Rt△ABC中，
（1）根据∠A＝75°，斜边AB＝6，你能求出这个直角三角形的其他元素吗？能6=75°在图中的Rt△ABC中，
（2）根据AC＝2.4，斜边AB＝6，你能求出这个直角三角形的其他元素吗？能62.4事实上，在直角三角形的六个元素中，除直角外，如果再知道两个元素（其中至少有一个是边），这个三角形就可以确定下来，这样就可以由已知的两个元素求出其余的三个元素．解直角三角形:在直角三角形中，由已知元素求未知元素的过程．在解直角三角形的过程中，一般要用到下面一些关系：解直角三角形（2）两锐角之间的关系∠A＋∠B＝90°（3）边角之间的关系（1）三边之间的关系 （勾股定理）在解直角三角形的过程中，一般要用到下面一些关系：例1 如图，在Rt△ABC中，∠C＝90°，
解这个直角三角形解：例2 如图，在Rt△ABC中，∠B＝35°，b=20，解这个直角三角形（精确到0.1）解：∠A＝90°－∠B＝90°－35°＝55°你还有其他方法求出c吗？例3 如图，在Rt△ABC中，∠C＝90°，AC=6， ∠BAC的平分线 ，解这个直角三角形。6解：因为AD平分∠BAC在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形；
（1）a = 30 , b = 20 ;练习解：根据勾股定理 在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形；
(2) ∠B＝72°，c = 14.解： 解决有关比萨斜塔倾斜的问题． 设塔顶中心点为B，塔身中心线与垂直中心线的夹角为A，过B点向垂直中心线引垂线，垂足为点C（如图），在Rt△ABC中，∠C＝90°，BC＝5.2m，AB＝54.5m所以∠A≈5°28′ 可以求出2001年纠偏后塔身中心线与垂直中心线的夹角．
你愿意试着计算一下吗？ABC解直角
三角形∠A＋ ∠ B＝90°a2+b2=c2三角函数
关系式计算器 由锐角求三角函数值由三角函数值求锐角解直角三角形：由已知元素求未知元素的过程直角三角形中，例4： 2008年10月15日“神舟”7号载人航天飞船发射成功．当飞船完成变轨后，就在离地球表面350km的圆形轨道上运行．如图，当飞船运行到地球表面上P点的正上方时，从飞船上最远能直接看到地球上的点在什么位置？这样的最远点与P点的距离是多少？（地球半径约为6 400km，结果精确到0.1km） 分析：从飞船上能最远直接看到的地球上的点，应是视线与地球相切时的切点． 如图，⊙O表示地球，点F是飞船的位置，FQ是⊙O的切线，切点Q是从飞船观测地球时的最远点． 的长就是地面上P、Q两点间的距离，为计算 的长需先求出∠POQ（即a）例题 解：在图中，FQ是⊙O的切线，△FOQ是直角三角形．∴ PQ的长为 当飞船在P点正上方时，从飞船观测地球时的最远点距离P点约2009.6km1. 如图，沿AC方向开山修路．为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B取∠ABD = 140°，BD = 520m，∠D=50°，那么开挖点E离D多远正好能使A，C，E成一直线（精确到0.1m）∴∠BED=∠ABD－∠D=90°答：开挖点E离点D 332.8m正好能使A，C，E成一直线.解：要使A、C、E在同一直线上，则 ∠ABD是 △BDE 的一个外角 2.　如图所示，一棵大树在一次强烈的地震中于离地面10米处折断倒下，树顶落在离树根24米处.大树在折断之前高多少？解　利用勾股定理可以求出折断倒下部分的长度为:
26＋10＝36（米）.
答:大树在折断之前高为36米.3. 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.30AB的长D（2）两锐角之间的关系∠A＋∠B＝90°（3）边角之间的关系（1）三边之间的关系 （勾股定理）在解直角三角形的过程中，一般要用到下面一些关系： -- 青岛版Thank You !9.5 解直角三角形的应用学习目标了解仰角、俯角的概念，能应用解直角三角形解决一类观测实际问题进一步了解数学建模思想，能将实际问题中的数量关系转化为直角三角形中元素之间的关系解直角
三角形∠A＋ ∠ B＝90°a2+b2=c2三角函数
关系式计算器 由锐角求三角函数值由三角函数值求锐角解直角三角形：由已知元素求未知元素的过程直角三角形中，解直角三角形的原则：（1）有角先求角，无角先求边（2）有斜用弦, 无斜用切； 宁乘毋除, 取原避中。【例1】直升飞机在跨江大桥AB的上方P点处，此时飞机离地面的高度PO=450米，且A、B、O三点在一条直线上，测得大桥两端的俯角分别为α=30°，β=45°，求大桥的长AB .PAB450米解：由题意得，答：大桥的长AB为 PAB400米答案: 米变题1：直升飞机在长400米的跨江大桥AB的上方P点处，且A、B、O三点在一条直线上，在大桥的两端测得飞机的仰角分别为30°和45 °，求飞机的高度PO .PBA200米C答案: 米变题2：直升飞机在高为200米的大楼AB上方P点处，从大楼的顶部和底部测得飞机的仰角为30°和60°，求飞机的高度PO .200米POBAD答案: 米变题3：直升飞机在高为200米的大楼AB左侧P点处，测得大楼的顶部仰角为45°,测得大楼底部俯角为30°，求飞机与大楼之间的水平距离.答案：AB≈520（米）变题4：（2008桂林）汶川地震后，抢险队派一架直升飞机去A、B两个村庄抢险，飞机在距地面450米上空的P点，测得A村的俯角为30°，B村的俯角为60°（如图5）．求A、B两个村庄间的距离．（结果精确到米，参考数据 ）.45°30°45045°30°40060°45°20020045°30°【例2】学生小王帮在测绘局工作的爸爸买了一些仪器后与同学在环西文化广场休息，看到濠河对岸的电视塔，他想用手中的测角仪和卷尺不过河测出电视塔空中塔楼的高度.现已测出∠ADB=40°，由于不能过河，因此无法知道BD的长度，于是他向前走50米到达C处测得∠ACB=55°，但他们在计算中碰到了困难，请大家一起想想办法，求出电视塔塔楼AB的高.（参考数据： ）答案：空中塔楼AB高约为105米【例3】 （2008芜湖）在我市迎接奥运圣火的活动中，某校教学楼上悬挂着宣传条幅DC，小丽同学在点A处，测得条幅顶端D的仰角为30°，再向条幅方向前进10米后， 又在点B处测得条幅顶端D的仰角为45°，已知点A、B和C离地面高度都为1.44米，求条幅顶端D点距离地面的高度．
（计算结果精确到0.1米） 参考数据:答案: 米简单实
际问题数学模型 直角三角形 三角形 梯形 组合图形构建解通过作高转化为直角三角形解数学建模及方程思想？1．把实际问题转化成数学问题，这个转化包括两个方面：一是将实际问题的图形转化为几何图形，画出正确的示意图；二是将已知条件转化为示意图中的边、角或它们之间的关系.2．把数学问题转化成解直角三角形问题，如果示意图不是直角三角形，可添加适当的辅助线，画出直角三角形.解题方法小结：2.如图2，在离铁塔BE 120m的A处，用测角仪测量塔顶的仰角为30°，已知测角仪高AD=1.5m，则塔高BE= _________ （根号保留）．1.如图1，已知楼房AB高为50m，铁塔塔基距楼房地基间的水平距离BD为100m，塔高CD为 m，则下面结论中正确的是（ ）
A．由楼顶望塔顶仰角为60°
B．由楼顶望塔基俯角为60°
C．由楼顶望塔顶仰角为30°
D．由楼顶望塔基俯角为30°C3.如图3，从地面上的C，D两点测得树顶A仰角分别是45°和30°，已知CD=200m，点C在BD上，则树高AB等于 （根号保留）．4.如图4，将宽为1cm的纸条沿BC折叠，使∠CAB=45°
，则折叠后重叠部分的面积为 （根号保留）． 思考2：有一块三形场地ABC，测得其中AB边长为60米，AC边长50米，∠ABC=30°，试求出这个三角形场地的面积．思考1：一架直升机从某塔顶Ａ测得地面C、D两点的俯角分别为30°、 45°，若C、D与塔底Ｂ共线，CD＝200米，求塔高AB？ABCDD′思考1：一架直升机从某塔顶Ａ测得地面C、D两点的俯角分别为30°、 45°，若C、D与塔底Ｂ共线，CD＝200米，求塔高AB？思考2：有一块三形场地ABC，测得其中AB边长为60米，AC边长50米，∠ABC=30°，试求出这个三角形场地的面积．作业必做题：
书本P96/4、P97/7题．
选做题：
1.一架直升机从某塔顶Ａ测得地面C、D两点的俯角分别为30°、 45°，若C、D与塔底Ｂ共线，CD＝200米，求塔高AB？
2.有一块三形场地ABC，测得其中AB边长为60米，AC边长50米，∠ABC=30°，试求出这个三角形场地的面积．3.（2008广安）如图，某幼儿园为了加强安全管理，决定将园内的滑滑板的倾角由45o降为30o，已知原滑滑板AB的长为5米，点D、B、C 在同一水平地面上．
（1）改善后滑滑板会加长多少？（精确到0．01）
（2）若滑滑板的正前方能有3米长的空地就能保证安全，原滑滑板的前方有6米长的空地，像这样改造是否可行？说明理由 (参考数据： ）视线视线仰角俯角在进行观察或测量时，仰角和俯角从上往下看，视线与水平线的夹角叫做俯角.从下向上看，视线与水平线的夹角叫做仰角； -- 青岛版谢谢大家!