第一章第一节集合第一课时[上学期]
文档属性
| 名称 | 第一章第一节集合第一课时[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 737.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-11 00:00:00 | ||
图片预览





文档简介
课件15张PPT。康托尔是德国数学家,
集合论的创始者。集合论是现代数学的基础,康托尔在研究
函数论时产生了探索无穷集和超穷数的兴趣。
康托尔肯定了无穷数的存在,并对无穷问题
进行了哲学的讨论,最终建立了较完善的集合
理论,为现代数学的发展打下了坚实的基础。
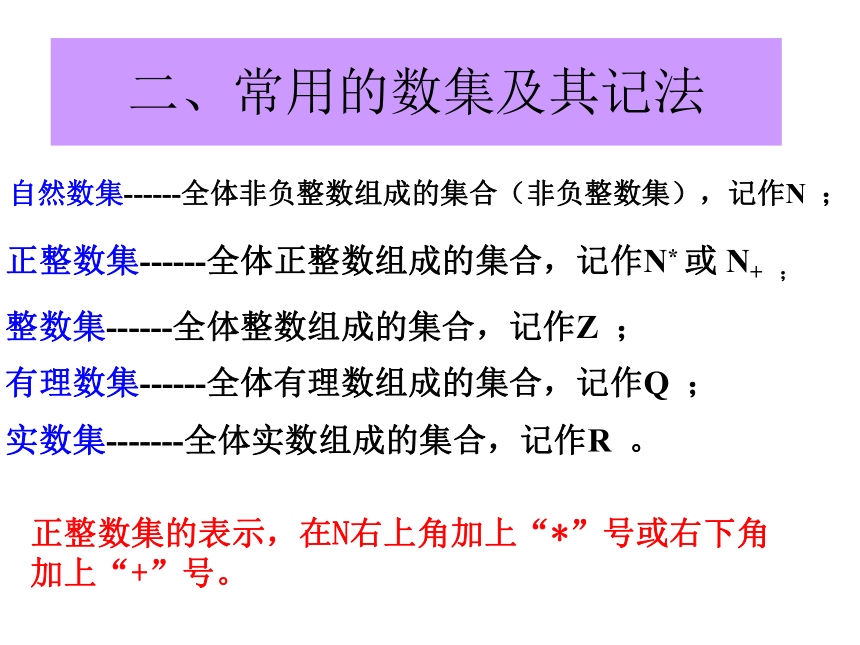
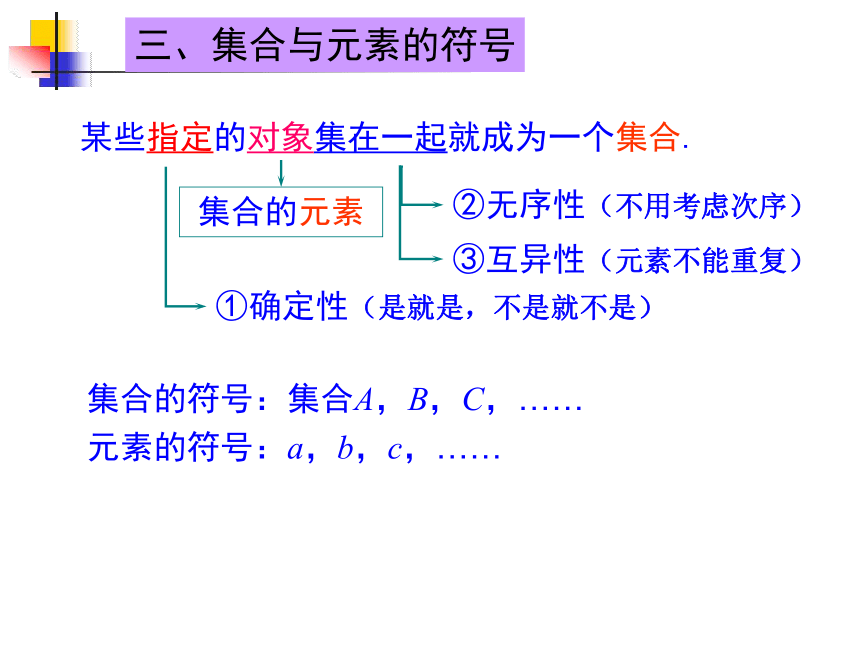
我们把研究对象统称为元素,把一些元素组成的总体叫做集合(简称为集)。一、集合的含义:二、常用的数集及其记法自然数集------全体非负整数组成的集合(非负整数集),记作N ;正整数集------全体正整数组成的集合,记作N* 或 N+ ;整数集------全体整数组成的集合,记作Z ; 有理数集------全体有理数组成的集合,记作Q ;实数集-------全体实数组成的集合,记作R 。正整数集的表示,在N右上角加上“*”号或右下角加上“+”号。 三、集合与元素的符号集合的符号:集合A,B,C,……元素的符号:a,b,c,……集合中的每个对象叫做这个集合的元素a A,m A,例如:设B={1,2,3,4,5},那么又如:属于记作不属于A记作四、集合的表示方法(1)1,2,3,4,5
(2)单位圆上所有的点
(3)所有直角三角形
(4)高一(15)班全体学生
(5)方程 x2-1=0的解
(6)不等式 x2-x-2>0的解—— {1,2,3,4,5}
—— {单位圆上的点}
—— {直角三角形}
—— {高一(15)班学生}
—— {x| x2-1=0}或{±1}
—— {x| x2-x-2>0 }1)列举法——把集合中的元素一一列举出来
2)描述法——通过描述集合所含元素的共同特征来表示集合(可以是文字,也可以是数学式)
{ x | x所满足的性质 }四、集合的表示方法3)图示法——韦恩图(或称文氏图)特别注意!
元素的无序性体现:
{1,2,3,4,5}与{2,5,4,3,1}是同一个集合.
元素的互异性体现:
① {1,2,3,4,5,1}是错误的;
② 集合{a,b}中必须满足a≠b .用一条封闭曲线围成的区域
表示一个集合例1、用列举法表示下列集合:
(1)小于10的所有自然数组成的集合;
(2)方程x2=x的所有实数根组成的集合;
(3)由1至20以内的所有质数组成的集合。思考:你能用列举法表示不等式x-7<3的解集吗?例2、试分别用列举法和描述法表示下列集合
(1)方程x2=x的所有实数根组成的集合;
(2)由大于10小于20的所有整数组成的集合。一般地、列举法适用于元素不太多的有限集,
而描述法适用于无限集五、集合的表示方法举例例 、 用适当的方法表示下列集合
(1)大于1小于10的偶数与质数所成的集合
(2)正有理数集
(3)偶数集
奇数集
正奇数集
能被3整除的整数
{x∈Q| x>0 }{x| x=2n,n∈Z }{x| x=2n+1,n∈Z }{x| x=2n+1,n∈N* }{x| x=3n,n∈N }练习、
1、课本第6页1、22、已知 求实数x的值3、若集合 仅有一个元素,
求实数a的值.思考:至多有一个元素呢?4、直角坐标系中,第二象限内的点构成的
集合为 。5、方程组 的解集是 。
(用两种方法表示)作业:课本第13页3、4课外作业:作业本A第1页再见
集合论的创始者。集合论是现代数学的基础,康托尔在研究
函数论时产生了探索无穷集和超穷数的兴趣。
康托尔肯定了无穷数的存在,并对无穷问题
进行了哲学的讨论,最终建立了较完善的集合
理论,为现代数学的发展打下了坚实的基础。
我们把研究对象统称为元素,把一些元素组成的总体叫做集合(简称为集)。一、集合的含义:二、常用的数集及其记法自然数集------全体非负整数组成的集合(非负整数集),记作N ;正整数集------全体正整数组成的集合,记作N* 或 N+ ;整数集------全体整数组成的集合,记作Z ; 有理数集------全体有理数组成的集合,记作Q ;实数集-------全体实数组成的集合,记作R 。正整数集的表示,在N右上角加上“*”号或右下角加上“+”号。 三、集合与元素的符号集合的符号:集合A,B,C,……元素的符号:a,b,c,……集合中的每个对象叫做这个集合的元素a A,m A,例如:设B={1,2,3,4,5},那么又如:属于记作不属于A记作四、集合的表示方法(1)1,2,3,4,5
(2)单位圆上所有的点
(3)所有直角三角形
(4)高一(15)班全体学生
(5)方程 x2-1=0的解
(6)不等式 x2-x-2>0的解—— {1,2,3,4,5}
—— {单位圆上的点}
—— {直角三角形}
—— {高一(15)班学生}
—— {x| x2-1=0}或{±1}
—— {x| x2-x-2>0 }1)列举法——把集合中的元素一一列举出来
2)描述法——通过描述集合所含元素的共同特征来表示集合(可以是文字,也可以是数学式)
{ x | x所满足的性质 }四、集合的表示方法3)图示法——韦恩图(或称文氏图)特别注意!
元素的无序性体现:
{1,2,3,4,5}与{2,5,4,3,1}是同一个集合.
元素的互异性体现:
① {1,2,3,4,5,1}是错误的;
② 集合{a,b}中必须满足a≠b .用一条封闭曲线围成的区域
表示一个集合例1、用列举法表示下列集合:
(1)小于10的所有自然数组成的集合;
(2)方程x2=x的所有实数根组成的集合;
(3)由1至20以内的所有质数组成的集合。思考:你能用列举法表示不等式x-7<3的解集吗?例2、试分别用列举法和描述法表示下列集合
(1)方程x2=x的所有实数根组成的集合;
(2)由大于10小于20的所有整数组成的集合。一般地、列举法适用于元素不太多的有限集,
而描述法适用于无限集五、集合的表示方法举例例 、 用适当的方法表示下列集合
(1)大于1小于10的偶数与质数所成的集合
(2)正有理数集
(3)偶数集
奇数集
正奇数集
能被3整除的整数
{x∈Q| x>0 }{x| x=2n,n∈Z }{x| x=2n+1,n∈Z }{x| x=2n+1,n∈N* }{x| x=3n,n∈N }练习、
1、课本第6页1、22、已知 求实数x的值3、若集合 仅有一个元素,
求实数a的值.思考:至多有一个元素呢?4、直角坐标系中,第二象限内的点构成的
集合为 。5、方程组 的解集是 。
(用两种方法表示)作业:课本第13页3、4课外作业:作业本A第1页再见
