人教A版(2019)必修第二册8.5.1 直线与直线平行 课件(共35张PPT)
文档属性
| 名称 | 人教A版(2019)必修第二册8.5.1 直线与直线平行 课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 844.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 04:06:51 | ||
图片预览



文档简介
(共35张PPT)
直线与直线平行
高一—人教A版—数学—必修二第八章
学习目标
理解并掌握基本事实4和等角定理;
能用基本事实4和等角定理解决一些简单的相关问题;
3.结合探究过程,体会平面图形的结论在空间图形中
推广的方法.
复习回顾
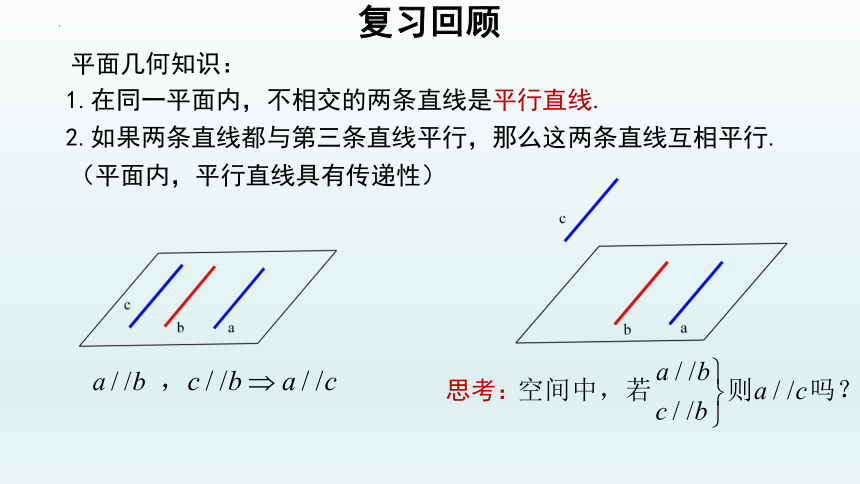
平面几何知识:
2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
1.在同一平面内,不相交的两条直线是平行直线.
(平面内,平行直线具有传递性)
思考:
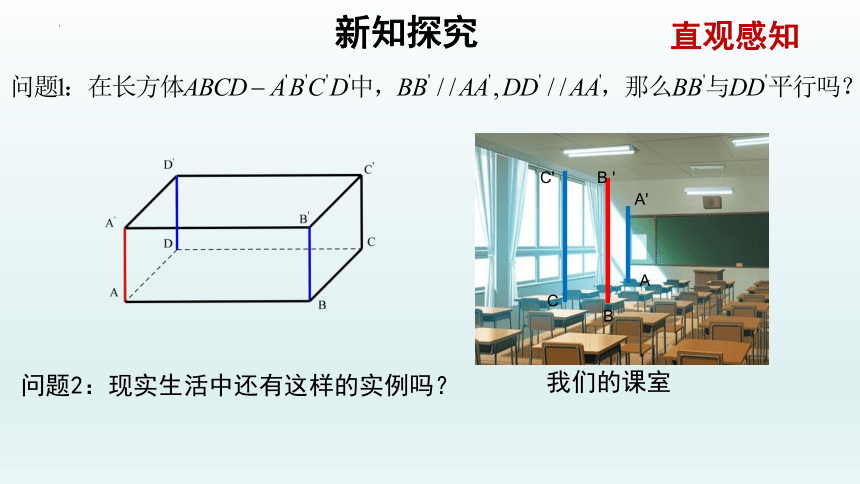
直观感知
问题2:现实生活中还有这样的实例吗?
A'
A
B '
B
C'
C
我们的课室
新知探究
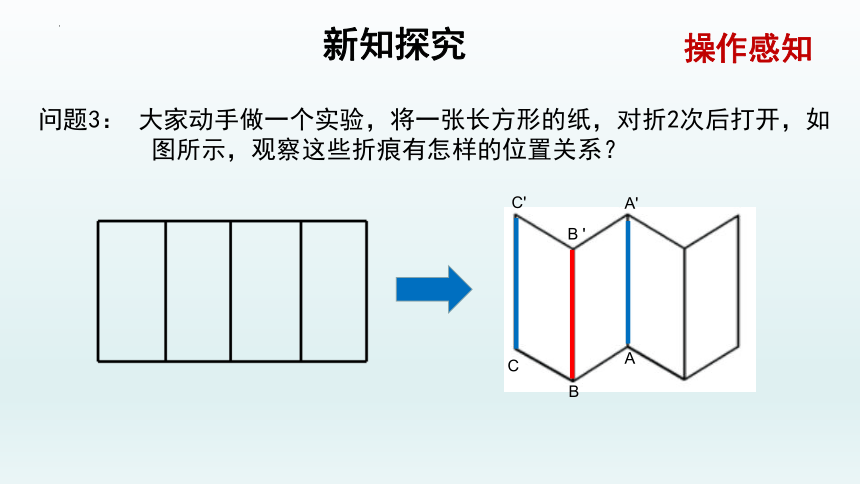
操作感知
问题3: 大家动手做一个实验,将一张长方形的纸,对折2次后打开,如图所示,观察这些折痕有怎样的位置关系?
A
B
C
新知探究
A'
B '
C'
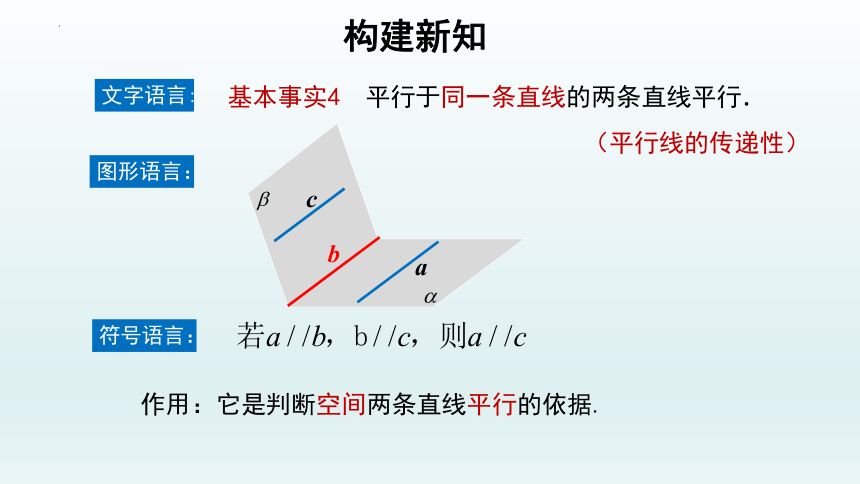
基本事实4 平行于同一条直线的两条直线平行.
作用:它是判断空间两条直线平行的依据.
a
c
b
文字语言:
图形语言:
符号语言:
(平行线的传递性)
构建新知
a
c
b
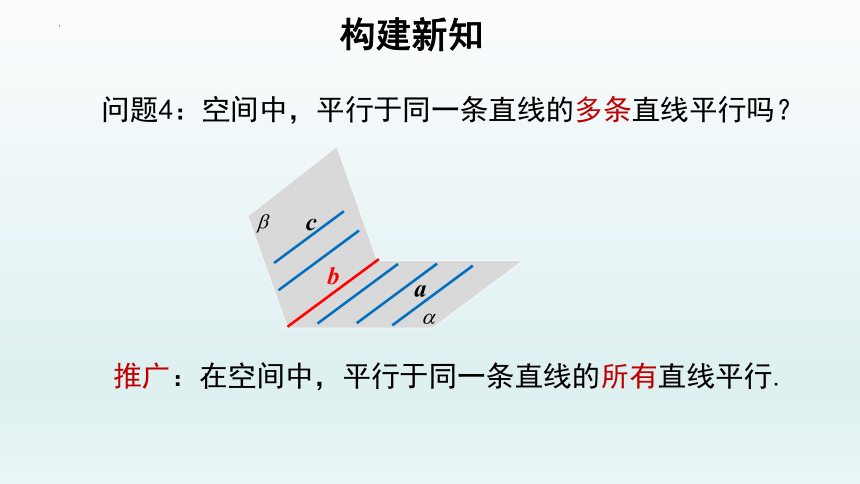
问题4:空间中,平行于同一条直线的多条直线平行吗?
推广:在空间中,平行于同一条直线的所有直线平行.
构建新知
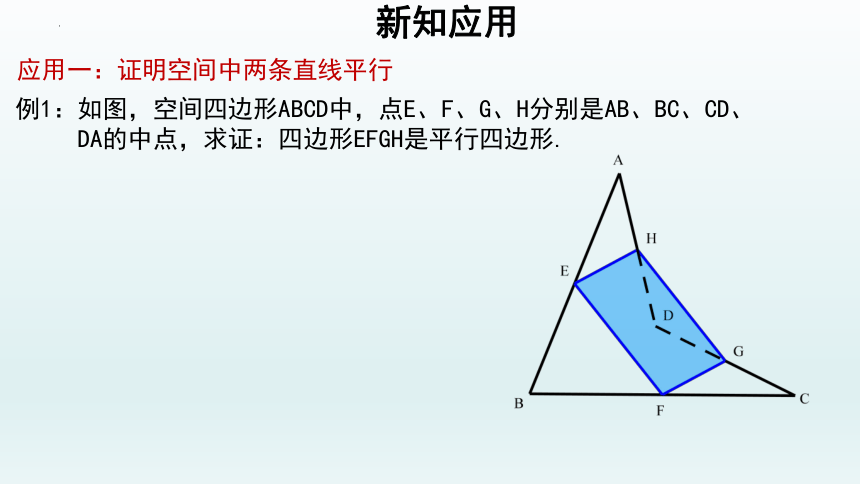
例1:如图,空间四边形ABCD中,点E、F、G、H分别是AB、BC、CD、
DA的中点,求证:四边形EFGH是平行四边形.
新知应用
应用一:证明空间中两条直线平行
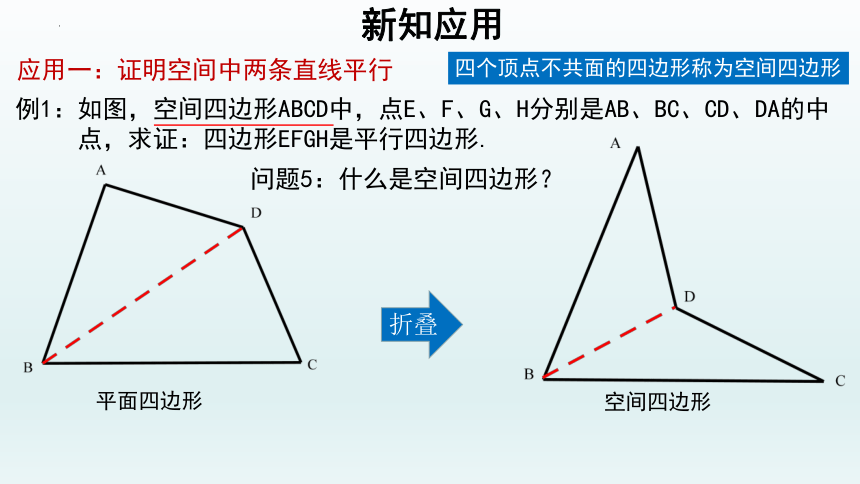
折叠
平面四边形
空间四边形
新知应用
应用一:证明空间中两条直线平行
例1:如图,空间四边形ABCD中,点E、F、G、H分别是AB、BC、CD、DA的中
点,求证:四边形EFGH是平行四边形.
问题5:什么是空间四边形?
四个顶点不共面的四边形称为空间四边形
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
例题讲解
应用一:证明空间中两条直线平行
四个顶点不共面的四边形称为空间四边形
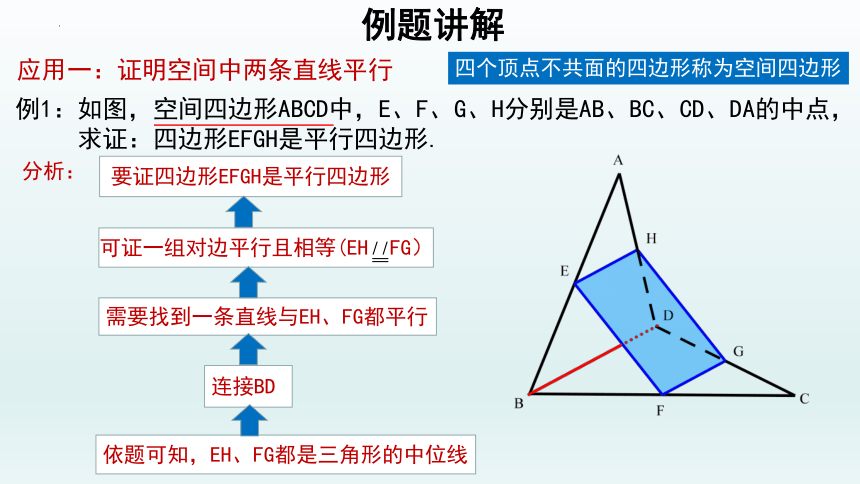
要证四边形EFGH是平行四边形
分析:
可证一组对边平行且相等(EH FG)
需要找到一条直线与EH、FG都平行
连接BD
依题可知,EH、FG都是三角形的中位线
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
证明:连接BD,
记得:证明过程,书写要规范哦!
例题讲解
应用一:证明空间中两条直线平行
四个顶点不共面的四边形称为空间四边形
因为 EH是 的中位线,
所以 EH//BD,且EH= BD
同理 FG//BD,且FG= BD
所以 四边形EFGH为平行四边形.
所以 EH FG,
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
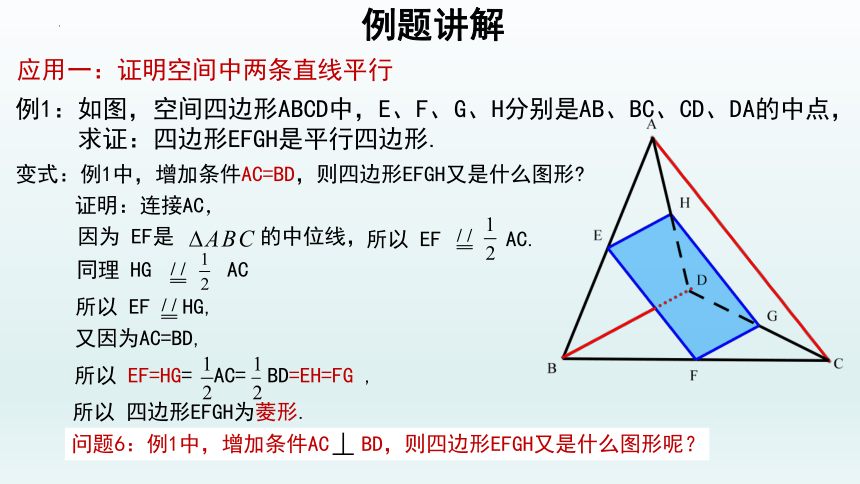
变式:例1中,增加条件AC=BD,则四边形EFGH又是什么图形
例题讲解
应用一:证明空间中两条直线平行
证明:连接AC,
因为 EF是 的中位线,
所以 EF AC.
所以 四边形EFGH为菱形.
又因为AC=BD,
所以 EF=HG= AC= BD=EH=FG ,
同理 HG AC
所以 EF HG,
问题6:例1中,增加条件AC BD,则四边形EFGH又是什么图形呢?
课堂练习
单选题:
B
判断题:在长方体 中,点E、F分别是AB,BC的中点,则EF与
是异面直线.( )
课堂练习
X
分析:
异面直线:不同在任何一个平面内,没有公共点
证明空间中两条直线平行的常用方法:
归纳提升
1.利用平面几何的知识来证明.(如三角形与梯形的中位线、
平行四边形的性质、平行线分线段成比例定理等)
2.利用基本事实4进行证明.(关键是找到“同一直线”b,
使得a∥b,同时c∥b,由此得到a∥c).
思考:“在平面内,如果一个角的两边与另一个角的两边分别对应平行,
则这两个角相等或互补.”在空间中,这一结论是否依然成立呢?
分析:在空间中,当两个角的两条边分别对应平行时,这两个角有以下两种位置:
当角两条边的方向都相同时,则两角相等
当角两条边的方向,一边相同,
一边相反时,则两角互补
大胆猜想:
在空间中该结论成立.
应用二:证明“等角定理”
新知探究
图(1)
图(2)
严谨求证?
思考:“在平面内,如果一个角的两边与另一个角的两边分别对应平行,
则这两个角相等或互补.”在空间中,这一结论是否依然成立呢?
应用二:证明“等角定理”
新知探究
图(1)
图(2)
大胆猜想:
在空间中该结论成立.
严谨求证?
已知:
求证:
思考:“在平面内,如果一个角的两边与另一个角的两边分别对应平行,
则这两个角相等或互补.”在空间中,这一结论是否依然成立呢?
应用二:证明“等角定理”
新知探究
图(1)
大胆猜想:
在空间中该结论成立
严谨求证?
已知:
求证:
分析:以第(1)种情况为例,
要证明
可以通过构造两个全等的
三角形来证明.
图(1)
已知:
求证:
第1种情况证明:分别在∠BAC和∠B'A'C'的两边上截取AD、AE和A'D'、A'E'
使得AD=A'D',AE=A'E'. 连接AA',DD',EE',DE,D'E',
新知探究
严谨证明
应用二:证明“等角定理”
已知:
求证:
第1种情况证明:分别在∠BAC和∠B'A'C'的两边上截取AD、AE和A'D'、A'E'
使得AD=A'D',AE=A'E'. 连接AA',DD',EE',DE,D'E',
∴四边形ADD'A'是平行四边形
同理可得
∴四边形EDD'E'是平行四边形
∴DE=D'E',
∴△DAE ≌ △D'A'E', ∴∠DAE=∠D'A'E'
∴∠BAC=∠B'A'C'.
新知探究
严谨证明
应用二:证明“等角定理”
已知:
求证:
新知探究
严谨证明
应用二:证明“等角定理”
思考:第2种情况,如何证明∠BAC与∠B'A'C'互补 ?
图(2)
分析:把∠B'A'C'的边A'C'进行反向延长,
转化为第1种情况进行证明,
已知:
求证:
新知探究
严谨证明
应用二:证明“等角定理”
思考:第2种情况,如何证明∠BAC与∠B'A'C'互补 ?
图(2)
分析:把∠B'A'C'的边A'C'进行反向延长,
转化为第1种情况的证明,
容易得到∠DAE与∠D'A'E'相等,
再由邻补角的性质,
得到∠BAC和∠B'A'C'互补,
问题得证.
等角定理:如果空间中两个角的两边分别对应平行,
那么这两个角相等或互补.
作用:用来判断或证明空间中两个角相等或互补.
图(1)
图(2)
构建新知
当角两条边的方向都相同时,则两角相等
当角两条边的方向,一边相同,
一边相反时,则两角互补
文字语言:
图形语言:
符号语言:
多选题(每小题给出的选项中,有多项符合题目的要求)
1.空间两个角 的两边分别对应平行,且 ,则 的大小可能是( )
A. B. C. D.
BD
解析:根据等角定理可知 为 或 .
课堂练习
多选题(每小题给出的选项中,有多项符合题目的要求)
2.下列结论中,正确的结论有( )
A.如果两条直线同时平行于第三条直线,那么这两条直线互相平行;
B.如果两个角相等,则它们的边互相平行;
C.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)
相等;
D.如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补.
课堂练习
AC
(基本事实4)
正方体
等边三角形
1.基本事实4:平行于同一条直线的两条直线平行。
2.等角定理 :如果空间中的两个角的两边分别平行,
则这两个角相等或互补。
作用:用来判断或证明空间两个角相等或互补的.
课堂小结
作用:它是判断空间两条直线平行的依据。
二.数学思想方法:
数形结合、特殊到一般、转化与化归、类比等数学思想.
一.知识内容:
课后作业
教材P135 练习第3、4题
2.教材P144 习题8.5 第9题
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
疑问1:例1中问题6的继续思考
变式2(问题6):例1中,增加条件AC⊥BD ,则四边形EFGH是什么图形
分析:
结论:已知两条异面直线a、b互相垂直,
在平面内取一点O,过点O作直线a、b的平行线,
则显然也有 成立.
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
证明:连接AC,
因为 EF是 的中位线,
所以 EF//AC.
所以四边形EFGH为矩形.
例1已经证明四边形EFGH是平行四边形,
又因为AC⊥BD ,所以
疑问1:例1的继续思考
因为 EH是 的中位线,
所以 EH//BD.
变式2:例1中,增加条件AC⊥BD ,则四边形EFGH是什么图形
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
疑问1:例1的继续思考
变式3:例1中,同时增加条件AC=BD AC⊥BD,则四边形EFGH是什么图形
四边形EFGH是一个正方形
疑问2:基本事实4、等角定理的综合应用
如图,在正方体ABCD -A1B1C1D1中,点M,M1分别是棱AD和A1D1的中点.
求证: ∠BMC =∠B1M1C1.
分析:
要证明两个角相等,可使用等角定理;
也可构造全等三角形或者相似三角形
进行证明;
∵在正方体ABCD- A1B1C1D1中,∴AD A1D1,
又因为M,M1分别为棱AD,A1D1的中点,
∴AM A1M1
疑问2:基本事实4、等角定理的综合应用
证明:连接MM1
又 ∵ AA1 BB1
如图,在正方体ABCD -A1B1C1D1中,点M,M1分别是棱AD和A1D1的中点.
求证: ∠BMC =∠B1M1C1.
∴MM1 AA1.
∴四边形AMM1A1为平行四边形,
∴ MM1 BB1,∴四边形MBB1M1为平行四边形.
∴MB//M1B1.
疑问2:基本事实4、等角定理的综合应用
如图,在正方体ABCD -A1B1C1D1中,点M,M1分别是棱AD和A1D1的中点.
求证: ∠BMC =∠B1M1C1.
同理可得四边形MCC1M1为平行四边形,
∴MC//M1C1.
∵∠BMC 和∠B1M1C1 方向相同,
∴∠BMC=∠B1M1C1.
基本事实4、等角定理都是由平面图形推广到立体图形得到的.
是否所有关于平面图形的结论都可以推广到空间呢?
例如:平面内,垂直于同一条直线的两条直线平行。
空间中,垂直于同一条直线的两条直线平行吗?
不成立。在空间中,垂直于同一条直线的两条直线平行、相交、异面.
注意:平面图形的结论要推广到空间图形,必须经过证明。
疑问3:
图(3)正方体
图(4)
图(5)
方法归纳
1.求证两角相等:
一是用等角定理;
二是用三角形全等或相似.
2.证明线线平行的常用方法:
(1)利用三角形、梯形中位线的性质.
(2)利用平行四边形的性质.
(3)利用平行线分线段成比例定理.
(4) 利用基本事实4.
3.平面图形的有关结论要推广到空间图形,必须经过证明.
直线与直线平行
高一—人教A版—数学—必修二第八章
学习目标
理解并掌握基本事实4和等角定理;
能用基本事实4和等角定理解决一些简单的相关问题;
3.结合探究过程,体会平面图形的结论在空间图形中
推广的方法.
复习回顾
平面几何知识:
2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
1.在同一平面内,不相交的两条直线是平行直线.
(平面内,平行直线具有传递性)
思考:
直观感知
问题2:现实生活中还有这样的实例吗?
A'
A
B '
B
C'
C
我们的课室
新知探究
操作感知
问题3: 大家动手做一个实验,将一张长方形的纸,对折2次后打开,如图所示,观察这些折痕有怎样的位置关系?
A
B
C
新知探究
A'
B '
C'
基本事实4 平行于同一条直线的两条直线平行.
作用:它是判断空间两条直线平行的依据.
a
c
b
文字语言:
图形语言:
符号语言:
(平行线的传递性)
构建新知
a
c
b
问题4:空间中,平行于同一条直线的多条直线平行吗?
推广:在空间中,平行于同一条直线的所有直线平行.
构建新知
例1:如图,空间四边形ABCD中,点E、F、G、H分别是AB、BC、CD、
DA的中点,求证:四边形EFGH是平行四边形.
新知应用
应用一:证明空间中两条直线平行
折叠
平面四边形
空间四边形
新知应用
应用一:证明空间中两条直线平行
例1:如图,空间四边形ABCD中,点E、F、G、H分别是AB、BC、CD、DA的中
点,求证:四边形EFGH是平行四边形.
问题5:什么是空间四边形?
四个顶点不共面的四边形称为空间四边形
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
例题讲解
应用一:证明空间中两条直线平行
四个顶点不共面的四边形称为空间四边形
要证四边形EFGH是平行四边形
分析:
可证一组对边平行且相等(EH FG)
需要找到一条直线与EH、FG都平行
连接BD
依题可知,EH、FG都是三角形的中位线
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
证明:连接BD,
记得:证明过程,书写要规范哦!
例题讲解
应用一:证明空间中两条直线平行
四个顶点不共面的四边形称为空间四边形
因为 EH是 的中位线,
所以 EH//BD,且EH= BD
同理 FG//BD,且FG= BD
所以 四边形EFGH为平行四边形.
所以 EH FG,
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
变式:例1中,增加条件AC=BD,则四边形EFGH又是什么图形
例题讲解
应用一:证明空间中两条直线平行
证明:连接AC,
因为 EF是 的中位线,
所以 EF AC.
所以 四边形EFGH为菱形.
又因为AC=BD,
所以 EF=HG= AC= BD=EH=FG ,
同理 HG AC
所以 EF HG,
问题6:例1中,增加条件AC BD,则四边形EFGH又是什么图形呢?
课堂练习
单选题:
B
判断题:在长方体 中,点E、F分别是AB,BC的中点,则EF与
是异面直线.( )
课堂练习
X
分析:
异面直线:不同在任何一个平面内,没有公共点
证明空间中两条直线平行的常用方法:
归纳提升
1.利用平面几何的知识来证明.(如三角形与梯形的中位线、
平行四边形的性质、平行线分线段成比例定理等)
2.利用基本事实4进行证明.(关键是找到“同一直线”b,
使得a∥b,同时c∥b,由此得到a∥c).
思考:“在平面内,如果一个角的两边与另一个角的两边分别对应平行,
则这两个角相等或互补.”在空间中,这一结论是否依然成立呢?
分析:在空间中,当两个角的两条边分别对应平行时,这两个角有以下两种位置:
当角两条边的方向都相同时,则两角相等
当角两条边的方向,一边相同,
一边相反时,则两角互补
大胆猜想:
在空间中该结论成立.
应用二:证明“等角定理”
新知探究
图(1)
图(2)
严谨求证?
思考:“在平面内,如果一个角的两边与另一个角的两边分别对应平行,
则这两个角相等或互补.”在空间中,这一结论是否依然成立呢?
应用二:证明“等角定理”
新知探究
图(1)
图(2)
大胆猜想:
在空间中该结论成立.
严谨求证?
已知:
求证:
思考:“在平面内,如果一个角的两边与另一个角的两边分别对应平行,
则这两个角相等或互补.”在空间中,这一结论是否依然成立呢?
应用二:证明“等角定理”
新知探究
图(1)
大胆猜想:
在空间中该结论成立
严谨求证?
已知:
求证:
分析:以第(1)种情况为例,
要证明
可以通过构造两个全等的
三角形来证明.
图(1)
已知:
求证:
第1种情况证明:分别在∠BAC和∠B'A'C'的两边上截取AD、AE和A'D'、A'E'
使得AD=A'D',AE=A'E'. 连接AA',DD',EE',DE,D'E',
新知探究
严谨证明
应用二:证明“等角定理”
已知:
求证:
第1种情况证明:分别在∠BAC和∠B'A'C'的两边上截取AD、AE和A'D'、A'E'
使得AD=A'D',AE=A'E'. 连接AA',DD',EE',DE,D'E',
∴四边形ADD'A'是平行四边形
同理可得
∴四边形EDD'E'是平行四边形
∴DE=D'E',
∴△DAE ≌ △D'A'E', ∴∠DAE=∠D'A'E'
∴∠BAC=∠B'A'C'.
新知探究
严谨证明
应用二:证明“等角定理”
已知:
求证:
新知探究
严谨证明
应用二:证明“等角定理”
思考:第2种情况,如何证明∠BAC与∠B'A'C'互补 ?
图(2)
分析:把∠B'A'C'的边A'C'进行反向延长,
转化为第1种情况进行证明,
已知:
求证:
新知探究
严谨证明
应用二:证明“等角定理”
思考:第2种情况,如何证明∠BAC与∠B'A'C'互补 ?
图(2)
分析:把∠B'A'C'的边A'C'进行反向延长,
转化为第1种情况的证明,
容易得到∠DAE与∠D'A'E'相等,
再由邻补角的性质,
得到∠BAC和∠B'A'C'互补,
问题得证.
等角定理:如果空间中两个角的两边分别对应平行,
那么这两个角相等或互补.
作用:用来判断或证明空间中两个角相等或互补.
图(1)
图(2)
构建新知
当角两条边的方向都相同时,则两角相等
当角两条边的方向,一边相同,
一边相反时,则两角互补
文字语言:
图形语言:
符号语言:
多选题(每小题给出的选项中,有多项符合题目的要求)
1.空间两个角 的两边分别对应平行,且 ,则 的大小可能是( )
A. B. C. D.
BD
解析:根据等角定理可知 为 或 .
课堂练习
多选题(每小题给出的选项中,有多项符合题目的要求)
2.下列结论中,正确的结论有( )
A.如果两条直线同时平行于第三条直线,那么这两条直线互相平行;
B.如果两个角相等,则它们的边互相平行;
C.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)
相等;
D.如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补.
课堂练习
AC
(基本事实4)
正方体
等边三角形
1.基本事实4:平行于同一条直线的两条直线平行。
2.等角定理 :如果空间中的两个角的两边分别平行,
则这两个角相等或互补。
作用:用来判断或证明空间两个角相等或互补的.
课堂小结
作用:它是判断空间两条直线平行的依据。
二.数学思想方法:
数形结合、特殊到一般、转化与化归、类比等数学思想.
一.知识内容:
课后作业
教材P135 练习第3、4题
2.教材P144 习题8.5 第9题
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
疑问1:例1中问题6的继续思考
变式2(问题6):例1中,增加条件AC⊥BD ,则四边形EFGH是什么图形
分析:
结论:已知两条异面直线a、b互相垂直,
在平面内取一点O,过点O作直线a、b的平行线,
则显然也有 成立.
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
证明:连接AC,
因为 EF是 的中位线,
所以 EF//AC.
所以四边形EFGH为矩形.
例1已经证明四边形EFGH是平行四边形,
又因为AC⊥BD ,所以
疑问1:例1的继续思考
因为 EH是 的中位线,
所以 EH//BD.
变式2:例1中,增加条件AC⊥BD ,则四边形EFGH是什么图形
例1:如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
疑问1:例1的继续思考
变式3:例1中,同时增加条件AC=BD AC⊥BD,则四边形EFGH是什么图形
四边形EFGH是一个正方形
疑问2:基本事实4、等角定理的综合应用
如图,在正方体ABCD -A1B1C1D1中,点M,M1分别是棱AD和A1D1的中点.
求证: ∠BMC =∠B1M1C1.
分析:
要证明两个角相等,可使用等角定理;
也可构造全等三角形或者相似三角形
进行证明;
∵在正方体ABCD- A1B1C1D1中,∴AD A1D1,
又因为M,M1分别为棱AD,A1D1的中点,
∴AM A1M1
疑问2:基本事实4、等角定理的综合应用
证明:连接MM1
又 ∵ AA1 BB1
如图,在正方体ABCD -A1B1C1D1中,点M,M1分别是棱AD和A1D1的中点.
求证: ∠BMC =∠B1M1C1.
∴MM1 AA1.
∴四边形AMM1A1为平行四边形,
∴ MM1 BB1,∴四边形MBB1M1为平行四边形.
∴MB//M1B1.
疑问2:基本事实4、等角定理的综合应用
如图,在正方体ABCD -A1B1C1D1中,点M,M1分别是棱AD和A1D1的中点.
求证: ∠BMC =∠B1M1C1.
同理可得四边形MCC1M1为平行四边形,
∴MC//M1C1.
∵∠BMC 和∠B1M1C1 方向相同,
∴∠BMC=∠B1M1C1.
基本事实4、等角定理都是由平面图形推广到立体图形得到的.
是否所有关于平面图形的结论都可以推广到空间呢?
例如:平面内,垂直于同一条直线的两条直线平行。
空间中,垂直于同一条直线的两条直线平行吗?
不成立。在空间中,垂直于同一条直线的两条直线平行、相交、异面.
注意:平面图形的结论要推广到空间图形,必须经过证明。
疑问3:
图(3)正方体
图(4)
图(5)
方法归纳
1.求证两角相等:
一是用等角定理;
二是用三角形全等或相似.
2.证明线线平行的常用方法:
(1)利用三角形、梯形中位线的性质.
(2)利用平行四边形的性质.
(3)利用平行线分线段成比例定理.
(4) 利用基本事实4.
3.平面图形的有关结论要推广到空间图形,必须经过证明.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
