苏教版(2019)选择性必修 第一册3.1.2 椭圆的几何性质 课件(共16张PPT)
文档属性
| 名称 | 苏教版(2019)选择性必修 第一册3.1.2 椭圆的几何性质 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 729.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 04:09:45 | ||
图片预览






文档简介
(共16张PPT)
椭圆的几何性质(一)
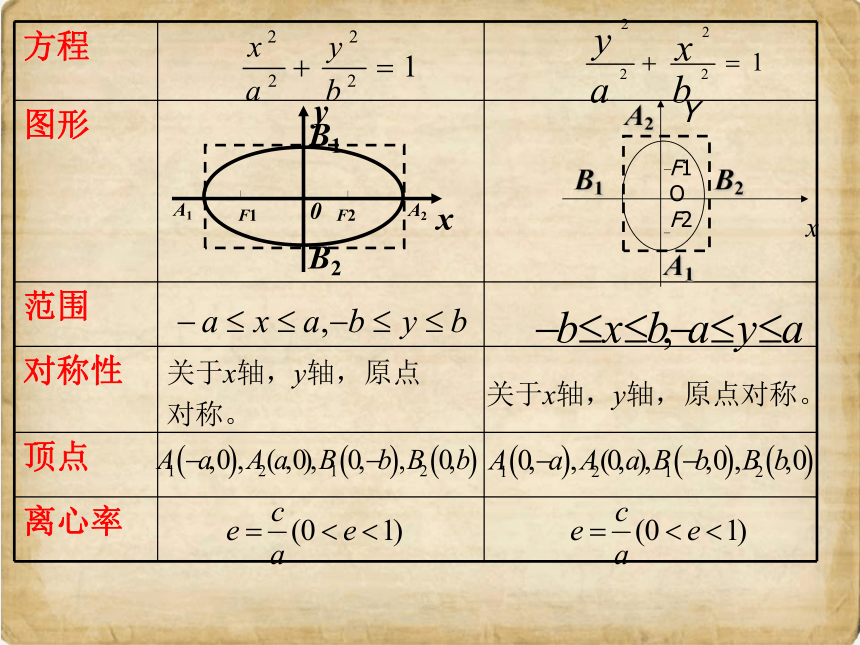
方程
图形
范围
对称性
顶点
离心率
x
y
B1
B2
A1
A2
∣ ∣
F1 F2
Y
x
F1
O
F2
_
_
A2
A1
B1
B2
0
关于x轴,y轴,原点
对称。
关于x轴,y轴,原点对称。
练习一:
1、说出下列椭圆的范围,长轴长,短轴长,焦点坐标,顶点坐标:
2、已知点P(3,6) 在上,则( )
(A) 点(-3,-6)不在椭圆上
(B) 点(3,-6)不在椭圆上
(C) 点(-3,6)在椭圆上
(D) 无法判断点(-3,-6), (3,-6), (-3,6)是否在椭圆上
3、判断下列方程所表示的曲线是否关于x轴,y 轴或原点对称
小结:如何判断一条曲线是否关于x轴,y轴或原点对称
如果用- x替换x ,方程不变,说明曲线关于y轴对称
如果用-y替换y,方程不变,说明曲线关于x轴对称
如果用- x. -y替换x. y ,方程不变,说明曲线关于原点对称
练习二:
1.比较下列每组中两个椭圆的形状,哪一个更扁
2. 已知方程
(1)它表示椭圆的充要条件是_________
(2)若它表示椭圆,则焦点坐标是_____________
(3)若离心率为0.5,则m 的值为___________
3. 当 三等分长轴 时,求离心率;
例1:如图:椭圆 (a>b>0)
当 为直角三角形时,求其离心率.
变式:
(1)当 为正三角形时,求其离心率;
(2) 当四边形 为正方形时,求其离心率;
(3) 过作椭圆的焦点作长轴的垂线交椭圆于点P,
若 为等腰直角三角形,求其离心率;
小结:如何求椭圆的离心率?
1.如果椭圆的方程已知,可直接求出a与c,从而求出离心率;
2.如果椭圆的方程未知,可寻找a与c的比例关系,常用的方法有:
(1 ) 找特征角
(2)利用定义
(3)根据已知条件,把几何关系转化为数量关系, 再通过列方程求解
(4) 从椭圆上一点Q作长轴的垂线,垂足为焦点 ,
且OQ//A2B2,求其离心率;
四.探究拓展:
如图: 是椭圆 的两个焦点,过
的弦AB与 组成等腰直角 ,其
中 ,求这个椭圆的离心率.
课堂小结:
1.知识点小结:
2.思想方法小结:
设在椭圆 (a>b>0)上有一点P,它与两个焦点的连
线互相垂直,求这个椭圆的离心率的取值范围.
作业:
椭圆的几何性质(一)
方程
图形
范围
对称性
顶点
离心率
x
y
B1
B2
A1
A2
∣ ∣
F1 F2
Y
x
F1
O
F2
_
_
A2
A1
B1
B2
0
关于x轴,y轴,原点
对称。
关于x轴,y轴,原点对称。
练习一:
1、说出下列椭圆的范围,长轴长,短轴长,焦点坐标,顶点坐标:
2、已知点P(3,6) 在上,则( )
(A) 点(-3,-6)不在椭圆上
(B) 点(3,-6)不在椭圆上
(C) 点(-3,6)在椭圆上
(D) 无法判断点(-3,-6), (3,-6), (-3,6)是否在椭圆上
3、判断下列方程所表示的曲线是否关于x轴,y 轴或原点对称
小结:如何判断一条曲线是否关于x轴,y轴或原点对称
如果用- x替换x ,方程不变,说明曲线关于y轴对称
如果用-y替换y,方程不变,说明曲线关于x轴对称
如果用- x. -y替换x. y ,方程不变,说明曲线关于原点对称
练习二:
1.比较下列每组中两个椭圆的形状,哪一个更扁
2. 已知方程
(1)它表示椭圆的充要条件是_________
(2)若它表示椭圆,则焦点坐标是_____________
(3)若离心率为0.5,则m 的值为___________
3. 当 三等分长轴 时,求离心率;
例1:如图:椭圆 (a>b>0)
当 为直角三角形时,求其离心率.
变式:
(1)当 为正三角形时,求其离心率;
(2) 当四边形 为正方形时,求其离心率;
(3) 过作椭圆的焦点作长轴的垂线交椭圆于点P,
若 为等腰直角三角形,求其离心率;
小结:如何求椭圆的离心率?
1.如果椭圆的方程已知,可直接求出a与c,从而求出离心率;
2.如果椭圆的方程未知,可寻找a与c的比例关系,常用的方法有:
(1 ) 找特征角
(2)利用定义
(3)根据已知条件,把几何关系转化为数量关系, 再通过列方程求解
(4) 从椭圆上一点Q作长轴的垂线,垂足为焦点 ,
且OQ//A2B2,求其离心率;
四.探究拓展:
如图: 是椭圆 的两个焦点,过
的弦AB与 组成等腰直角 ,其
中 ,求这个椭圆的离心率.
课堂小结:
1.知识点小结:
2.思想方法小结:
设在椭圆 (a>b>0)上有一点P,它与两个焦点的连
线互相垂直,求这个椭圆的离心率的取值范围.
作业:
