第一章第二节第一课时子集,真子集[上学期]
文档属性
| 名称 | 第一章第二节第一课时子集,真子集[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 438.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-11 23:42:00 | ||
图片预览






文档简介
课件22张PPT。集合间的基本关系问:浙江省在什么地方?问:中国的区域与浙江省的区域有何关系? 如果我们把浙江省的区域用集合A来表示,中国区域用集合B来表示,则A在集合B内;也就是说集合A的每一个元素都在集合B内。 请列举类似的例子观察以下每组中的两个集合A、B,看看这两个集合中的元素有什么关系:
(1)A={1,2},B={1,2,3}
(2)A=N,B=R
(3)A={x ︱x为北京人}
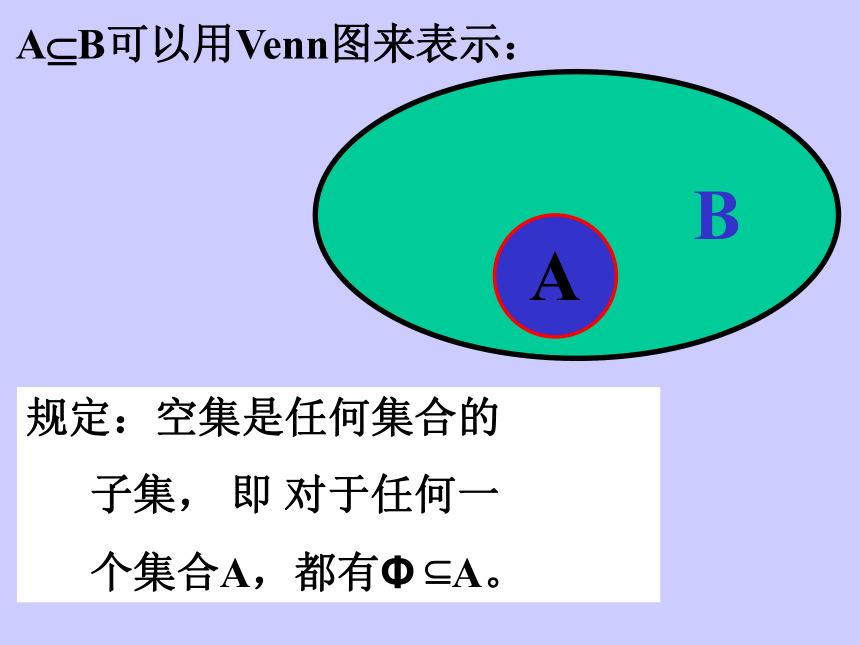
B={x ︱x为中国人} 以上几组集合中,集合A中的元素都在集合B中。对于集合A中的任何一个元素都是集合B的元素(若a∈A,则a∈B ),则称集合A是集合B的子集(subset)。记作A?B,或B?A。读作“集合A包含于集合B”或“集合B包含集合A”用数学语言来表示就是:若x∈A,则x∈B,我们就说A是B的子集。记作A?B,或B?A。一、子集A?B可以用Venn图来表示:规定:空集是任何集合的
子集, 即 对于任何一
个集合A,都有Φ ?A。思考:A?B与B?A是否同时成立?设A={x|x是两条边相等的三角形}
B={x|x是等腰三角形}A与B是什么关系?A=B一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,记作A=B。用数学语言来表述上面的话就是:若A?B,且B?A,
则A=B。二、集合相等集合相等的定义1:课本第3页对于两个集合A与B,如果A?B,且A≠B,我们就说A是B的真子集(proper set),记作 。读作A真包含于B(或B真包含A)。我们也可以这样说:如果集合A是集合B的子集,并且集合B中至少有一个元素不是集合A的元素,那么A是B的真子集。三、真子集集合A=B和A真包含于B可以用下面的图形来表示:ABA=B BAA真包含于B根据子集的定义,易知子集具有以下性质:(1) Φ ? A(空集是任何集合的子集)。(2)A ? A(任何一个集合是它本身的子集)(3)若A ?B,B ?C,则A ?C(包含关系
具有传递性)。类似地,真子集具有以下性质:(1)若A≠ Φ,则Φ真包含于A(空集是任何非空集合的真子集)。(2)若A 真包含于B,B 真包含于C, 则A 真包含于C(真包含关系也具有传递性)。例1、写出集合{a,b} 的所有子集。解:集合{a,b} 的所有子集为Φ,{a},{b},{a,b}。写出集合{a,b,c,d} 的所有真子集。写出集合{a,b,c,} 的所有真子集。元素个数与集合子集个数的关系:一般地,若集合A中有n个元素,则集合A有 个子集, -1个非空子集, -1个真子集, -2个非空真子集。课本第8页练习1、2、3例2、已知{a,b}?A真包含于{a,b,c,d}求所有满足条件的集合A。解:∵{a,b}?A,∴A中必有元素a,b。
又∵ A?{a,b,c,d},
∴A中的元素有2个或3个。
因此满足条件的集合A有:
{a,b},{a,b,c},{a,b,d}。例3、已知A={x︱x<3},B={x︱x<a}
(1)若B?A,求a的取值范围。
(2)若A? B,求a的取值范围。分析:本题是将不等式的知识与集合的内容联系起来,通过不等式在数轴上的表示即可获解。解:(1)∵ B?A,如右图,
∴a≤3。(2)∵ A ? B, 如右图,∴a 3。
例4、已知A={1,x,y},B={x,x ,xy},
且A=B,求实数x,y。分析:此题从集合A中的已知数1入手,因
为A=B,则B中必有1,根据元素的互异性
知,x≠1,故x =1,或xy=1,从而分别求
出x,y的值。注意所求值是否使集合元素
满足互异性是这类题容易忽略而引起错解
的地方。 解:由A={1,x,y}可知,x≠1,y≠1。
∵A=B,∴① 或②
由①得 或 (舍)
由②得 (舍)。
故综上所述,x = -1,y=0。再分析:由于本题给出的两个相等的集合
是有限集,故可根据相等的有限集的性
质:(1)两个集合的所有元素之和相等;
(2)两个集合的所有元素之积相等。
列出关于x,y的方程组,求解即可。解法二、∵A=B,
∴依题义有
即
由集合中元素的互异性可知:x≠1,x≠0,
∴解方程组得x = -1,y=0。例5、设A={x︱x –8x+15=0},
B={x︱ax –1=0},若B?A,
求实数 a 组成的集合。分析:易知A={3,5},而集合B为一个一
次方程的解集,因此集合B中最多有一
个元素,有因为B?A,所以B= Φ或{3}或{5},由此便可解出 a 的值。小结:再见
(1)A={1,2},B={1,2,3}
(2)A=N,B=R
(3)A={x ︱x为北京人}
B={x ︱x为中国人} 以上几组集合中,集合A中的元素都在集合B中。对于集合A中的任何一个元素都是集合B的元素(若a∈A,则a∈B ),则称集合A是集合B的子集(subset)。记作A?B,或B?A。读作“集合A包含于集合B”或“集合B包含集合A”用数学语言来表示就是:若x∈A,则x∈B,我们就说A是B的子集。记作A?B,或B?A。一、子集A?B可以用Venn图来表示:规定:空集是任何集合的
子集, 即 对于任何一
个集合A,都有Φ ?A。思考:A?B与B?A是否同时成立?设A={x|x是两条边相等的三角形}
B={x|x是等腰三角形}A与B是什么关系?A=B一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,记作A=B。用数学语言来表述上面的话就是:若A?B,且B?A,
则A=B。二、集合相等集合相等的定义1:课本第3页对于两个集合A与B,如果A?B,且A≠B,我们就说A是B的真子集(proper set),记作 。读作A真包含于B(或B真包含A)。我们也可以这样说:如果集合A是集合B的子集,并且集合B中至少有一个元素不是集合A的元素,那么A是B的真子集。三、真子集集合A=B和A真包含于B可以用下面的图形来表示:ABA=B BAA真包含于B根据子集的定义,易知子集具有以下性质:(1) Φ ? A(空集是任何集合的子集)。(2)A ? A(任何一个集合是它本身的子集)(3)若A ?B,B ?C,则A ?C(包含关系
具有传递性)。类似地,真子集具有以下性质:(1)若A≠ Φ,则Φ真包含于A(空集是任何非空集合的真子集)。(2)若A 真包含于B,B 真包含于C, 则A 真包含于C(真包含关系也具有传递性)。例1、写出集合{a,b} 的所有子集。解:集合{a,b} 的所有子集为Φ,{a},{b},{a,b}。写出集合{a,b,c,d} 的所有真子集。写出集合{a,b,c,} 的所有真子集。元素个数与集合子集个数的关系:一般地,若集合A中有n个元素,则集合A有 个子集, -1个非空子集, -1个真子集, -2个非空真子集。课本第8页练习1、2、3例2、已知{a,b}?A真包含于{a,b,c,d}求所有满足条件的集合A。解:∵{a,b}?A,∴A中必有元素a,b。
又∵ A?{a,b,c,d},
∴A中的元素有2个或3个。
因此满足条件的集合A有:
{a,b},{a,b,c},{a,b,d}。例3、已知A={x︱x<3},B={x︱x<a}
(1)若B?A,求a的取值范围。
(2)若A? B,求a的取值范围。分析:本题是将不等式的知识与集合的内容联系起来,通过不等式在数轴上的表示即可获解。解:(1)∵ B?A,如右图,
∴a≤3。(2)∵ A ? B, 如右图,∴a 3。
例4、已知A={1,x,y},B={x,x ,xy},
且A=B,求实数x,y。分析:此题从集合A中的已知数1入手,因
为A=B,则B中必有1,根据元素的互异性
知,x≠1,故x =1,或xy=1,从而分别求
出x,y的值。注意所求值是否使集合元素
满足互异性是这类题容易忽略而引起错解
的地方。 解:由A={1,x,y}可知,x≠1,y≠1。
∵A=B,∴① 或②
由①得 或 (舍)
由②得 (舍)。
故综上所述,x = -1,y=0。再分析:由于本题给出的两个相等的集合
是有限集,故可根据相等的有限集的性
质:(1)两个集合的所有元素之和相等;
(2)两个集合的所有元素之积相等。
列出关于x,y的方程组,求解即可。解法二、∵A=B,
∴依题义有
即
由集合中元素的互异性可知:x≠1,x≠0,
∴解方程组得x = -1,y=0。例5、设A={x︱x –8x+15=0},
B={x︱ax –1=0},若B?A,
求实数 a 组成的集合。分析:易知A={3,5},而集合B为一个一
次方程的解集,因此集合B中最多有一
个元素,有因为B?A,所以B= Φ或{3}或{5},由此便可解出 a 的值。小结:再见
