23.3实践与探索(共2课时)
图片预览









文档简介
课件30张PPT。华东师大版
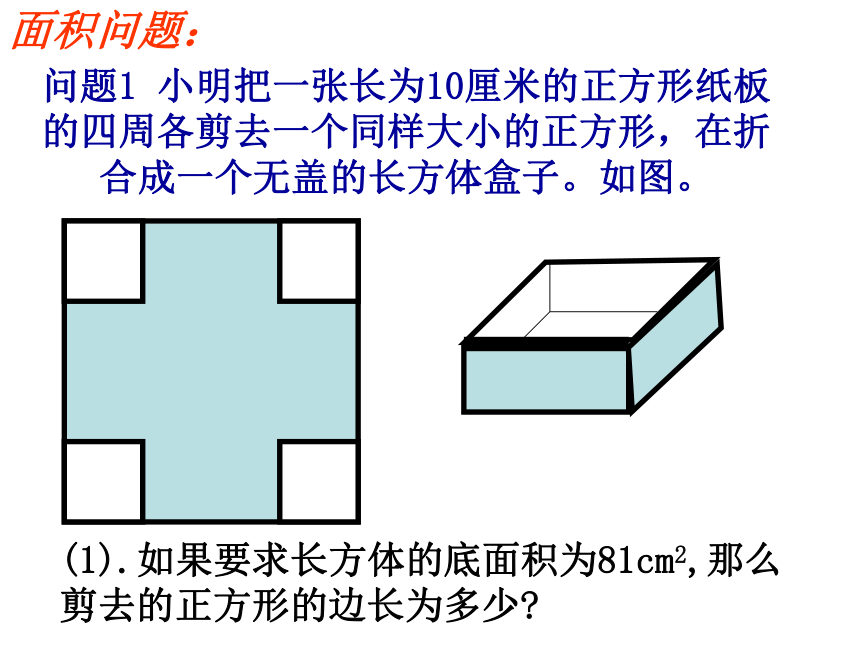
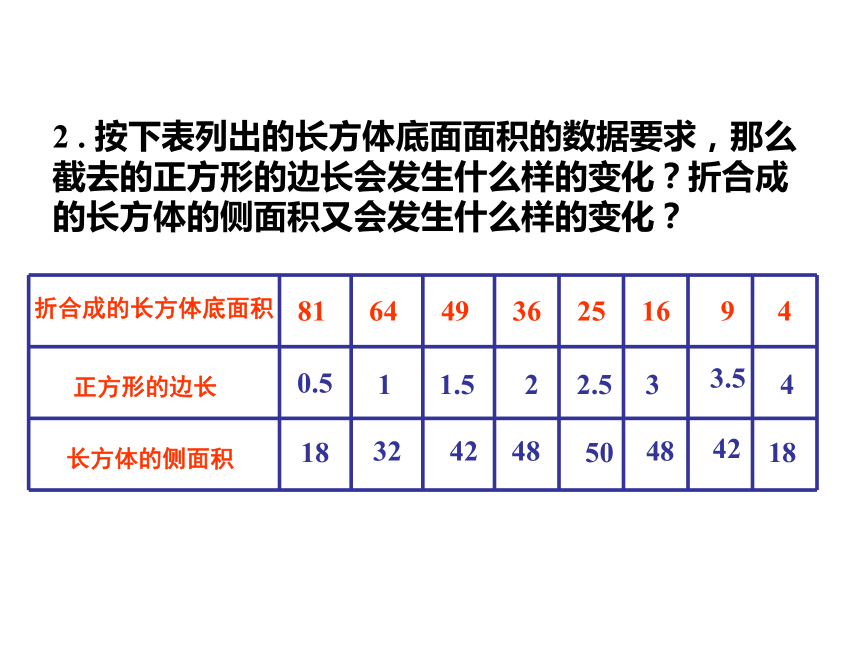
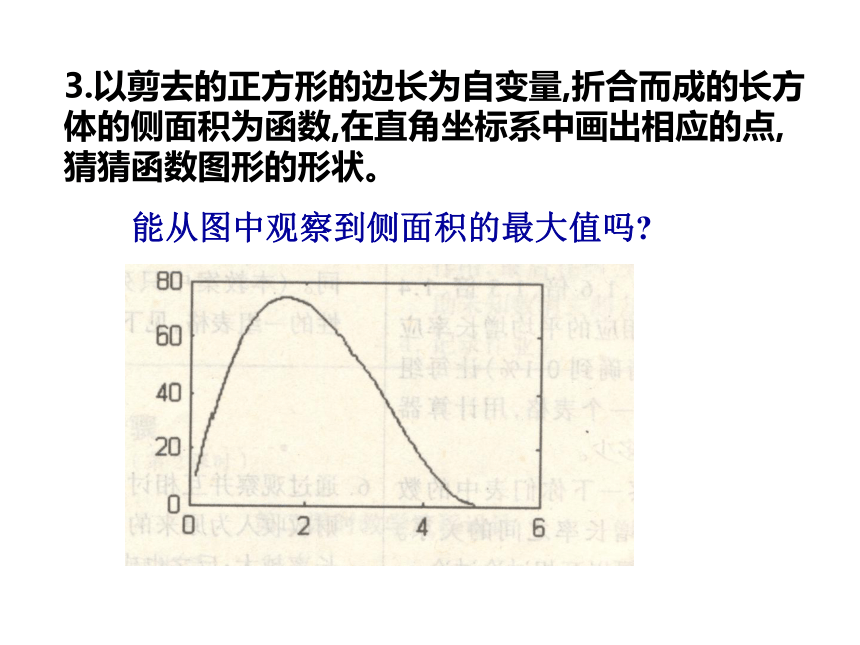
九年级(上)数学教学课件23.3实践与探索(第1课时)华东师大版九年级第23章 一元二次方程面积问题:问题1 小明把一张长为10厘米的正方形纸板的四周各剪去一个同样大小的正方形,在折合成一个无盖的长方体盒子。如图。(1).如果要求长方体的底面积为81cm2,那么剪去的正方形的边长为多少?2 . 按下表列出的长方体底面面积的数据要求,那么截去的正方形的边长会发生什么样的变化?折合成的长方体的侧面积又会发生什么样的变化?1321.5482.534240.51842250483.5183.以剪去的正方形的边长为自变量,折合而成的长方体的侧面积为函数,在直角坐标系中画出相应的点,猜猜函数图形的形状。能从图中观察到侧面积的最大值吗?自主探究1、现有长方体塑料片一块,19cm,宽15cm,给你锋利小刀一把,粘胶、直尺、你能做一个底面积为77cm2的无盖的长方体水槽吗?说说你是怎样做的?2、如图,一个院子长10m,宽8m,要在它的里面沿三边辟出宽度相等的花圃,使花圃的面积等于院子面积的30%,试求这花圃的宽度。(花圃的宽度为1m)解:设这花圃的宽度为x,依题意,得问题2:阳江市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?1、翻一番,你是如何理解的?(翻一番,即为原净收入的2倍,若设原值为1,那么两年后的值就是2) 2、“平均年增长率”你是如何理解的。(“平均年增长率”指的是每一年净收入增长的百分数是一个相同的值。即每年按同样的百分数增加)增长率问题问题1 因为增长率不能为负数
所以增长率应为, 问题2:阳江市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?答:这两年中财政净收入的平均年增长率约为41.4%2、若调整计划,两年后的财政净收入值为原值的1.5倍、1.2倍、…,那么两年中的平均年增长率相应地调整为多少?3、又若第二年的增长率为第一年的2倍,那么第一年的增长率为多少时可以实现市财政净收入翻一番? 1.某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,这两个月平均每月增长的百分率是多少?解:设平均每月增长的百分率为,
依题意,得因为不合题意所以只能取答:平均每月增长的百分率是 20%. 2. 某种药品,原来每盒售价96元,由于两次降价;现在每盒售价54元。平均每次降价百分之几?解:设平均每次降价的百分率为x,依题意,得答:平均每次降价的百分率是 25%。小结 谈谈你对本节所探讨的知识有何体会,你能否结合你的体会编制一道应用题,在小组内交流 。23.3探索与实践(第2课时)华东师大版九年级第23章 一元二次方程一元二次方程 ax2+bx+c=0(a≠0) 的求根公式: x=(b2-4ac≥ 0)回顾算一算(1)x2-7x+12=0(2)x2+3x-4=0(3) 2x2+3x-2=0解下列方程并完成填空:341271-3- 4- 4-1-2一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,那么x1+x2= , x1x2= 注:能用根与系数的关系的前提条件为b2-4ac≥0一元二次方程根与系数关系的证明:X1+x2=+==X1x2=●===如果方程x2+px+q=0的两根是
x1 ,x2,那么x1+x2= ,
x1x2=-Pq推论解:①② 我能行1原方程可化为:二次项不是1,可以先把它化为1∴原方程可化为:想一想,还有其他方法吗?还可以把 代入方程的两边,求出 解:∴又∵ 我能行2①②解: 我能行3所求的方程是:解: 我能行4即:或:(1)下列方程两根的和与两根的积各是多少?知识在于积累知识在于积累(4)求一个一元二次方程,使它的两个根分别为:
;②①根与系数关系小结1、已知方程的一个根求另一个根及未知数(也可以用根的定义求解)对于一元二次方程 的两根2、求关于两根的代数式的值如:两根的平方和、两根的倒数和等3、以x1、x2 为根的一元二次方程
x2-(x1+x2)x+x1x2=0,拓广探索1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1∵ (x2-x1)2=(x1+x2)2-4x1x2由根与系数的关系得x1+x2= , x1x2=∴解得k1=9,k2= -3当k=9或-3时,由于b2-4ac≥0,∴k的值为9或-3。拓广探索2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。解:由方程有两个实数根,得即-8k+4≥0由根与系数的关系得x1+x2= 2(k-1) , x1x2=k2∴ X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4由X12+x22 =4,得2k2-8k+4=4解得k1=0 , k2=4经检验, k2=4不合题意,舍去。∴ k=0小结1. 这节课我们学习了哪些知识?2. 我们会用这些知识完成什么类型的习题?
九年级(上)数学教学课件23.3实践与探索(第1课时)华东师大版九年级第23章 一元二次方程面积问题:问题1 小明把一张长为10厘米的正方形纸板的四周各剪去一个同样大小的正方形,在折合成一个无盖的长方体盒子。如图。(1).如果要求长方体的底面积为81cm2,那么剪去的正方形的边长为多少?2 . 按下表列出的长方体底面面积的数据要求,那么截去的正方形的边长会发生什么样的变化?折合成的长方体的侧面积又会发生什么样的变化?1321.5482.534240.51842250483.5183.以剪去的正方形的边长为自变量,折合而成的长方体的侧面积为函数,在直角坐标系中画出相应的点,猜猜函数图形的形状。能从图中观察到侧面积的最大值吗?自主探究1、现有长方体塑料片一块,19cm,宽15cm,给你锋利小刀一把,粘胶、直尺、你能做一个底面积为77cm2的无盖的长方体水槽吗?说说你是怎样做的?2、如图,一个院子长10m,宽8m,要在它的里面沿三边辟出宽度相等的花圃,使花圃的面积等于院子面积的30%,试求这花圃的宽度。(花圃的宽度为1m)解:设这花圃的宽度为x,依题意,得问题2:阳江市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?1、翻一番,你是如何理解的?(翻一番,即为原净收入的2倍,若设原值为1,那么两年后的值就是2) 2、“平均年增长率”你是如何理解的。(“平均年增长率”指的是每一年净收入增长的百分数是一个相同的值。即每年按同样的百分数增加)增长率问题问题1 因为增长率不能为负数
所以增长率应为, 问题2:阳江市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?答:这两年中财政净收入的平均年增长率约为41.4%2、若调整计划,两年后的财政净收入值为原值的1.5倍、1.2倍、…,那么两年中的平均年增长率相应地调整为多少?3、又若第二年的增长率为第一年的2倍,那么第一年的增长率为多少时可以实现市财政净收入翻一番? 1.某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,这两个月平均每月增长的百分率是多少?解:设平均每月增长的百分率为,
依题意,得因为不合题意所以只能取答:平均每月增长的百分率是 20%. 2. 某种药品,原来每盒售价96元,由于两次降价;现在每盒售价54元。平均每次降价百分之几?解:设平均每次降价的百分率为x,依题意,得答:平均每次降价的百分率是 25%。小结 谈谈你对本节所探讨的知识有何体会,你能否结合你的体会编制一道应用题,在小组内交流 。23.3探索与实践(第2课时)华东师大版九年级第23章 一元二次方程一元二次方程 ax2+bx+c=0(a≠0) 的求根公式: x=(b2-4ac≥ 0)回顾算一算(1)x2-7x+12=0(2)x2+3x-4=0(3) 2x2+3x-2=0解下列方程并完成填空:341271-3- 4- 4-1-2一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,那么x1+x2= , x1x2= 注:能用根与系数的关系的前提条件为b2-4ac≥0一元二次方程根与系数关系的证明:X1+x2=+==X1x2=●===如果方程x2+px+q=0的两根是
x1 ,x2,那么x1+x2= ,
x1x2=-Pq推论解:①② 我能行1原方程可化为:二次项不是1,可以先把它化为1∴原方程可化为:想一想,还有其他方法吗?还可以把 代入方程的两边,求出 解:∴又∵ 我能行2①②解: 我能行3所求的方程是:解: 我能行4即:或:(1)下列方程两根的和与两根的积各是多少?知识在于积累知识在于积累(4)求一个一元二次方程,使它的两个根分别为:
;②①根与系数关系小结1、已知方程的一个根求另一个根及未知数(也可以用根的定义求解)对于一元二次方程 的两根2、求关于两根的代数式的值如:两根的平方和、两根的倒数和等3、以x1、x2 为根的一元二次方程
x2-(x1+x2)x+x1x2=0,拓广探索1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1∵ (x2-x1)2=(x1+x2)2-4x1x2由根与系数的关系得x1+x2= , x1x2=∴解得k1=9,k2= -3当k=9或-3时,由于b2-4ac≥0,∴k的值为9或-3。拓广探索2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。解:由方程有两个实数根,得即-8k+4≥0由根与系数的关系得x1+x2= 2(k-1) , x1x2=k2∴ X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4由X12+x22 =4,得2k2-8k+4=4解得k1=0 , k2=4经检验, k2=4不合题意,舍去。∴ k=0小结1. 这节课我们学习了哪些知识?2. 我们会用这些知识完成什么类型的习题?
