3.2 一元二次不等式及其解法课件
文档属性
| 名称 | 3.2 一元二次不等式及其解法课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 248.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-18 00:00:00 | ||
图片预览






文档简介
课件16张PPT。 一元二次不等式及其解法高中数学必修5 两个网络服务公司(Internet Serice Provider)的资费标准:
电信:每小时收费1.5元
网通:用户上网的第一小时内收费1.7元,第二小时内收费1.6元,以后每小时减少0.1元.(若用户一次上网时间超过17小时,按17小时计算)?
<不妨设该同学一次上网不超过17小时>
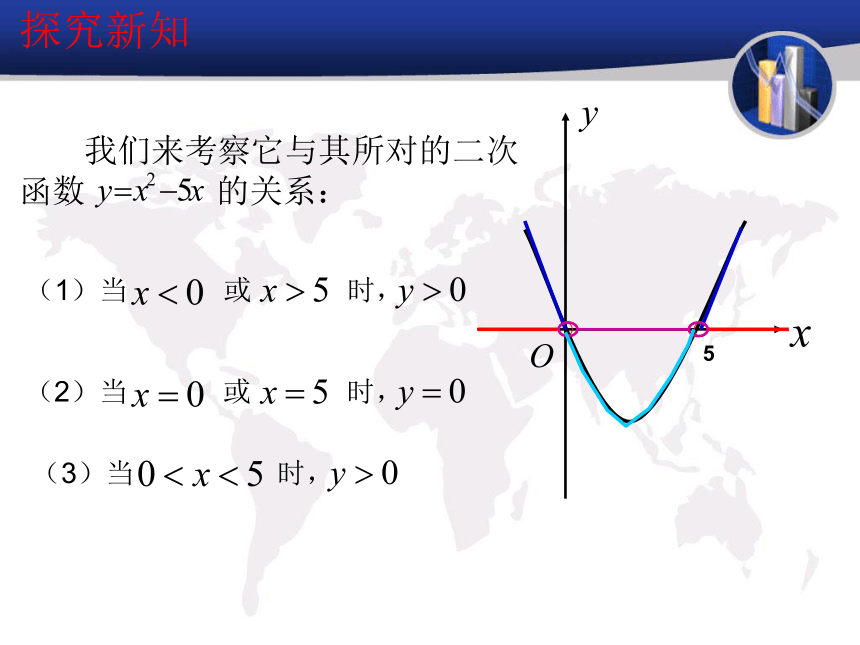
一次上网在多长时间以内能够保证选择电信比选择网通所需费用少?新课导入分析:假设一次上网x小时,∴网通公司的收取费用为如果能够保证选择电信公司比选择网通公司所需费用少,则整理得新课导入则电信公司的收取费用为1.5x根据题意知,网通收费1.7 ,1.6,1.5 ,1.4,……这是什么?一元二次不等式新知讲解 象 这样只含一个未知数,并且未知数最高次数为2的不等式。探究新知思考: 那么一元二次不等式 怎样去求解呢?探究新知 我们来考察它与其所对的二次
函数 的关系:(1)当 或 时,(2)当 或 时,(3)当 时,5下结论:
结合图像知不等式 的解集
是推广:
那么对于一般的不等式
或 又怎样去寻求解集呢?一元二次不等式的解法△>0△=0△<0有两相异实根
x1, x2 (x1 x1=x2=没有实根{x|xx2}{x|x1< x 考虑判别式:计算判别式的值,若值为正,则求出相应方程的两根;
下结论:注意结果要写成集合或者区间的形式课堂练习 这节课我们学习了一元二次不等式的解法,同学们下去可以多注意以下两点1、三个二次的关系,注意结合图像;
2、将一元二次不等式化为标准形式;课堂小结作业:
课本80页习题3.2 A组第1、2题
谢谢例2、求函数 的定义域例题讲解解:要使得函数有意义,则 ,即: ,也即故函数 的定义域是 。探究新知 我们来考察它与其所对的二次
函数 的关系:(1)当 或 时,(2)当 或 时,(3)当 时,●●y>0,x轴上方y<0,x轴下方y=0,x轴上5
电信:每小时收费1.5元
网通:用户上网的第一小时内收费1.7元,第二小时内收费1.6元,以后每小时减少0.1元.(若用户一次上网时间超过17小时,按17小时计算)?
<不妨设该同学一次上网不超过17小时>
一次上网在多长时间以内能够保证选择电信比选择网通所需费用少?新课导入分析:假设一次上网x小时,∴网通公司的收取费用为如果能够保证选择电信公司比选择网通公司所需费用少,则整理得新课导入则电信公司的收取费用为1.5x根据题意知,网通收费1.7 ,1.6,1.5 ,1.4,……这是什么?一元二次不等式新知讲解 象 这样只含一个未知数,并且未知数最高次数为2的不等式。探究新知思考: 那么一元二次不等式 怎样去求解呢?探究新知 我们来考察它与其所对的二次
函数 的关系:(1)当 或 时,(2)当 或 时,(3)当 时,5下结论:
结合图像知不等式 的解集
是推广:
那么对于一般的不等式
或 又怎样去寻求解集呢?一元二次不等式的解法△>0△=0△<0有两相异实根
x1, x2 (x1
下结论:注意结果要写成集合或者区间的形式课堂练习 这节课我们学习了一元二次不等式的解法,同学们下去可以多注意以下两点1、三个二次的关系,注意结合图像;
2、将一元二次不等式化为标准形式;课堂小结作业:
课本80页习题3.2 A组第1、2题
谢谢例2、求函数 的定义域例题讲解解:要使得函数有意义,则 ,即: ,也即故函数 的定义域是 。探究新知 我们来考察它与其所对的二次
函数 的关系:(1)当 或 时,(2)当 或 时,(3)当 时,●●y>0,x轴上方y<0,x轴下方y=0,x轴上5
