函数的单调性[上学期]
图片预览




文档简介
课件10张PPT。教者: guoyumin函数的单调性1. 什么是在某一区间上的(单调)增函数?什么是在某一区间上的(单调)减函数?它们在图像上有怎样的(直观)特征?2. 什么是函数的单调区间?单调区间与函数的单调性有什么联系? 阅读教材P48~49相关内容,回答下列问题:3. 一个函数在其定义域内是否一定具有相同的单调性?举例说明。函数的单调性: ★如果一个函数在某个区间M上是增函数或减函数,那么就说这个函数在这个区间M具有单调性 (区间M称为单调区间)。设函数f(x) 的定义域为A,区间M A。如果取区间M
中的任意两个值x1,x2,则
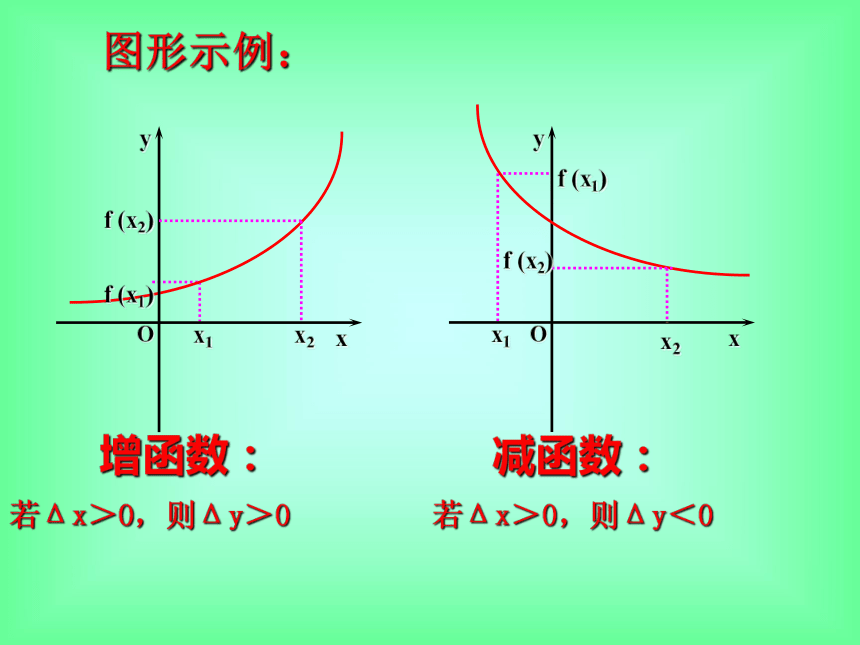
当改变量Δx=x2-x1>0,有Δy=f(x2)-f(x1)>0,那么就称函数y=f(x)在 区间M上是增函数。
当改变量Δx=x2-x1>0,有Δy=f(x2)-f(x1)<0,那么就称函数y=f(x)在 区间M上是减函数。图形示例:增函数:减函数:若Δx>0,则Δy>0若Δx>0,则Δy<0例. P48 例题1、2,P50练习A、B例题与练习:练习: 判断函数f (x)=-2x+7在其定义域内的单调性,并且加以证明。思考: 函数f (x) =ax+b(a≠0)在定义域内有怎样的单调性?例. 证明函数f (x)=x2-4x-3在(-∞,2]上是减函数。例题与练习:练习: 判断函数f (x)=-x2+2x-7的单调区间,并对其增区间加以证明。思考: 函数f (x) =ax2+bx+c(a≠0)在定义域内有怎样的单调性?例题与练习:练习: 判断函数f (x)= 在其定义域内的单调性,并且加以证明。思考1: 函数f (x) = (a≠0)在定义域内有怎样的单调性?思考2: 函数f (x) = 在定义域内有怎样的单调性?例. 证明函数f (x)= 在(-∞,3)上是减函数。练习: 判断函数f (x)= 的单调区间,并对其中的一个区间加以证明。再 见
中的任意两个值x1,x2,则
当改变量Δx=x2-x1>0,有Δy=f(x2)-f(x1)>0,那么就称函数y=f(x)在 区间M上是增函数。
当改变量Δx=x2-x1>0,有Δy=f(x2)-f(x1)<0,那么就称函数y=f(x)在 区间M上是减函数。图形示例:增函数:减函数:若Δx>0,则Δy>0若Δx>0,则Δy<0例. P48 例题1、2,P50练习A、B例题与练习:练习: 判断函数f (x)=-2x+7在其定义域内的单调性,并且加以证明。思考: 函数f (x) =ax+b(a≠0)在定义域内有怎样的单调性?例. 证明函数f (x)=x2-4x-3在(-∞,2]上是减函数。例题与练习:练习: 判断函数f (x)=-x2+2x-7的单调区间,并对其增区间加以证明。思考: 函数f (x) =ax2+bx+c(a≠0)在定义域内有怎样的单调性?例题与练习:练习: 判断函数f (x)= 在其定义域内的单调性,并且加以证明。思考1: 函数f (x) = (a≠0)在定义域内有怎样的单调性?思考2: 函数f (x) = 在定义域内有怎样的单调性?例. 证明函数f (x)= 在(-∞,3)上是减函数。练习: 判断函数f (x)= 的单调区间,并对其中的一个区间加以证明。再 见
