6.1.1 空间向量的线性运算(word版含答案)
文档属性
| 名称 | 6.1.1 空间向量的线性运算(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 723.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 18:10:37 | ||
图片预览



文档简介
第6章
空间向量与立体几何
向量是具有大小和方向的量,这一概念既适用于平面,也适用于空间.空间向量的引入,为处理立体几何问题提供了新的视角,它是研究空间图形位置关系和度量问题的有力工具.本章我们在必修第二册“平面向量”的基础上,利用类比方法,学习空间向量的概念、运算(包括线性运算和数量积)、基本定理,并运用空间向量研究空间基本图形的平行、垂直等位置关系和距离、角度等度量问题.学习本章时应重视以下方面:第一,类比的方法.引导学生经历向量及其运算由平面向空间的推广过程.第二,直线的方向向量和平面的法向量的重要作用.第三,程序思想方法(即通性通法).通过用向量法求空间角和距离的解决过程,体会程序思想方法的优越性.
本章重点提升学生的直观想象、数学运算、逻辑推理素养.
6.1.1 空间向量的线性运算
知识技能
1. 了解空间向量及其线性运算由平面向空间推广的过程,掌握空间向量的线性运算及其性质.
2. 掌握空间向量共线的概念及定理.
思想方法
类比平面向量及其线性运算,尝试研究空间向量及其线性运算,建构空间向量及其线性运算的知识结构,发现并归纳它们的异同点.
核心素养
1. 将平面向量向空间推广的过程中,提升逻辑推理素养.
2. 在线性运算中提升数学运算素养.
教学重点:空间向量的概念、空间向量的线性运算及其运算律.
教学难点:空间向量的线性运算及其运算律.
问题导引
预习教材P5~7,思考下面的问题:
1. 什么是空间向量?如何表示空间向量?
2. 空间向量线性运算的运算法则和运算律有哪些?
3. 共线向量定理的内容是什么?
4. 空间向量与前面所学的平面向量有什么共性内容?
即时体验
1. (多选)下列等式中正确的是(ABD)
A. a+0=a
B. a+b=b+a
C. +=0
D. =++
2. 给出下列命题:
① 向量的长度与向量的长度相等;
② 若向量a与向量b平行,则a与b的方向相同或相反;
③ 两个有共同起点并且长度相等的向量的终点必相同;
④ 两个有共同终点的向量一定是共线向量;
⑤ 若向量与向量是共线向量,则A, B, C三点必在同一条直线上;
⑥ 有向线段就是向量,向量就是有向线段.
其中假命题有_4__个.
一、 问题情境
如图1,湖面上有三个景点O, A, B,一游艇将游客从景点O送至景点A,半小时后,游艇再将游客送至景点B.从景点O到景点A有一个位移,从景点A到景点B也有一个位移.
(图1)
问题1游客的位移与路程是否相同?(从大小与方向两方面考虑)
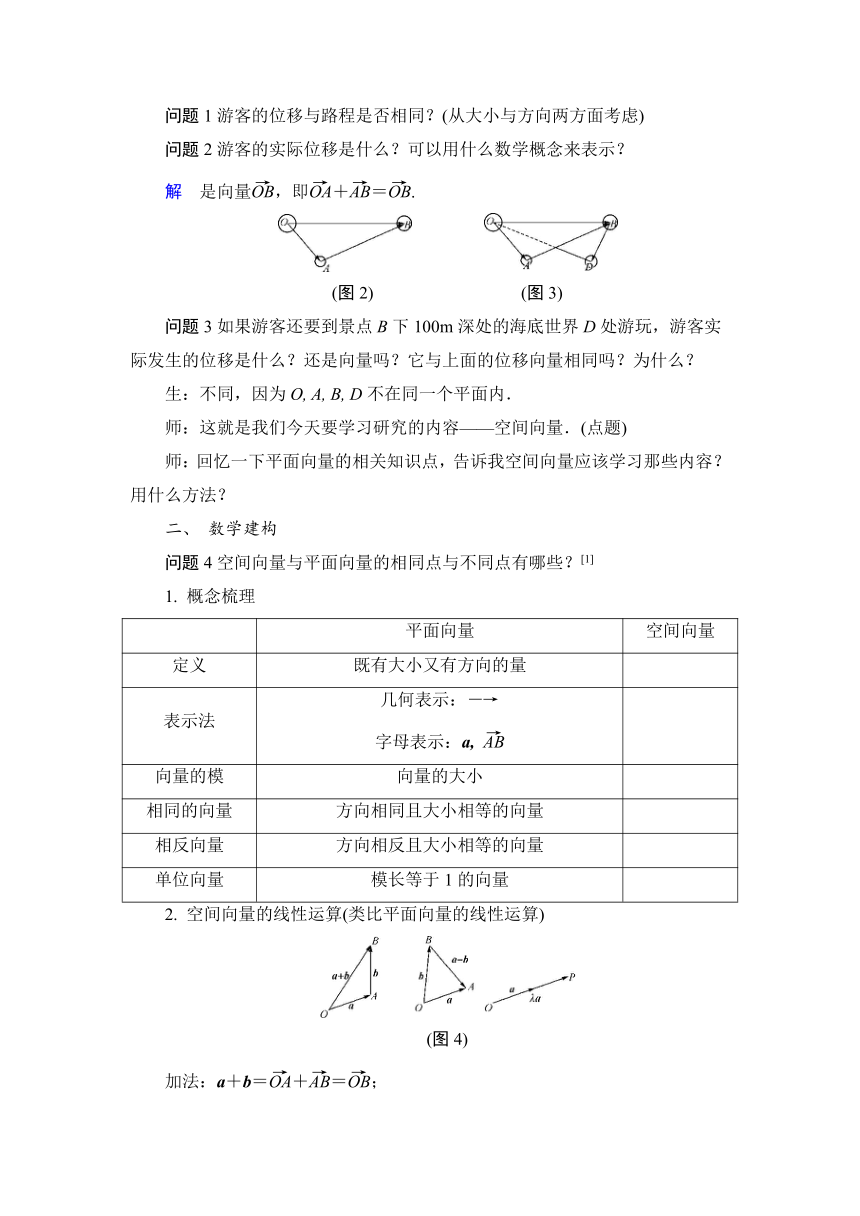
问题2游客的实际位移是什么?可以用什么数学概念来表示?
解 是向量,即+=.
(图2) (图3)
问题3如果游客还要到景点B下100m深处的海底世界D处游玩,游客实际发生的位移是什么?还是向量吗?它与上面的位移向量相同吗?为什么?
生:不同,因为O, A, B, D不在同一个平面内.
师:这就是我们今天要学习研究的内容——空间向量.(点题)
师:回忆一下平面向量的相关知识点,告诉我空间向量应该学习那些内容?用什么方法?
二、 数学建构
问题4空间向量与平面向量的相同点与不同点有哪些?[1]
1. 概念梳理
平面向量 空间向量
定义 既有大小又有方向的量
表示法 几何表示:―→ 字母表示:a,
向量的模 向量的大小
相同的向量 方向相同且大小相等的向量
相反向量 方向相反且大小相等的向量
单位向量 模长等于1的向量
2. 空间向量的线性运算(类比平面向量的线性运算)
(图4)
加法:a+b=+=;
减法:a-b=-=;
数乘:λa=(λ∈R).
3. 空间向量的运算律(类比平面向量的运算律)
(图5)
(1) 加法交换律:a+b=b+a;
(2) 加法结合律:(a+b)+c=a+(b+c);
(3) 数乘分配律:λ(a+b)=λa+λb(λ∈R).
4. 共线(平行)向量
(1) 定义:如果表示空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫作共线向量或平行向量.
记作:a ∥b.
规定:零向量与任意向量共线.
(2) 共线向量定理:对空间任意两个向量a, b(a≠0), b与a共线的充要条件是存在实数λ,使b=λa.
三、 数学运用
例1 (教材P6例1)如图,在三棱柱ABC A1B1C1中,M是BB1的中点.化简下列各式,并在图中标出化简得到的向量.
(例1)
(1) +; (2) ++;
(3) --.[2]
(见学生用书课堂本P1)
[处理建议] 运用向量加减法的三角形法则,若其中某个向量无法直接运用法则,则先将其化为适合法则的向量再运算.
[规范板书] 解 (1) +=.
(2) 因为M是BB1的中点,所以=.又=,所以++=+=.
(3) --=-=.
向量, , ,如图所示.
(1) ++…+An-1An=;
(2) ++…+An-1An+= 0 .
[题后反思] 注意:若有多个向量参与运算,按照“尾首相接,首尾相联”的原则进行运算.
例2 如图,在正方体ABCD A1B1C1D1中,点E是上底面A1B1C1D1的中心.若=m+n+,求m, n的值.[3]
(见学生用书课堂本P2)
(例2)
[处理建议] 引导学生将问题转化为向量如何用向量, , 表示,即可求得m, n的值.
[规范板书] 解 因为点E是上底面A1B1C1D1的中心,所以=(+)=(+)=+.又因为+=,所以m=n=.
在平行六面体ABCD A′B′C′D′中,若=x++,则x+y+z=_6__.
[规范板书] 解 在平行六面体ABCD A′B′C′D′中,=++,而=x++, 所以 得 所以x+y+z=6.
[题后反思] 逆向思维及转化思想是解决数学问题常用的方法.
例3 如图,在三棱锥A BCD中,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ∥平面BCD.[4]
(见学生用书课堂本P2)
(例3)
[处理建议] 利用空间向量共线的定义,证明线线平行及线面平行问题.
[规范板书] 证明 过点P, Q分别作PS∥AD交BD于点S, QT∥AD交CD于点T,连接ST,则=, =.因为=,所以=,所以四边形PQTS是平行四边形,则=.所以PQ∥ST.又因为PQ 平面BCD, ST 平面BCD,所以PQ∥平面BCD.
[题后反思] 将立体几何中的平行问题化归为向量共线问题,是解决立体几何中证明题的常用方法.
已知E, F, G, H分别为四面体ABCD的棱AB, BC, CD, DA的中点,且E, F, G, H四点共面,求证:BD∥平面EFGH.
(变式)
[规范板书] 证明 因为=-=-=,所以EH∥BD.又因为EH 平面EFGH, BD 平面EFGH,所以BD∥平面EFGH.
例4 设e1,e2是空间两个不共线的非零向量,已知=2e1+ke2, =e1+3e2, =2e1-e2,且A, B, D三点共线,求实数k的值.[5]
[处理建议] A, B, D三点共线即=λ,转化为向量共线问题进而求得k的值.
[规范板书] 解 =e1+3e2, =2e1-e2,故=+=(e1+3e2)+(-2e1+e2)=-e1+4e2. 因为A, B, D三点共线,所以=λ,即2e1+ke2=λ(-e1+4e2). 因为e1,e2是不共线的向量,所以 得k=-8.
[题后反思] 点共线问题可转化为向量共线问题来求解,再充分运用向量共线的充要条件“a=λb”和向量运算法则来解题.
已知e1, e2是空间两个不共线的非零向量,且=e1+ke2, =e1+3e2, =2e1-e2,若A, B, D三点共线,则k=-4.
四、 课堂练习
1. 化简:+++= 0 .
2. 在正方体ABCD A1B1C1D1中,下面化简后为零向量的是(A)
A. ++
B. -+
C. ++
D. +
3. (多选)已知正方体ABCD A1B1C1D1的中心为O,则下列结论正确的有(ACD)
A. +与+是一对相反向量
B. -与-是一对相反向量
C. +++与+++是一对相反向量
D. -与-是一对相反向量
4. 如图,在平行六面体ABCD A1B1C1D1中,G为△A1BD的重心.设=a, =b, =c,则=a+b+c.(用a, b, c表示)
(第4题)
提示 =+=+(+)=+(-)+(-)=++=a+b+c.
5. 如图,已知四边形ABCD与ABEF都是平行四边形且不共面,M, N分别是AC, BF的中点,判断与是否共线.
(第5题)
解 由题意知=++=++, =+++=-+--,两式相加得2=, 所以与共线.
五、 课堂小结
1. 空间向量的基本概念、线性运算及其运算律.
2. 运用类比的思想,掌握平面向量与空间向量的异同点.
[1] 阅读教材P5~6,要求学生通读一遍,精读一遍,复读一遍,然后完成下表.
[2] 此题主要是帮助学生熟悉空间向量的线性运算,熟练掌握运算法则,为后续学习奠定扎实的基础.
[3] 此题注重培养学生的转化思维方式,进一步巩固空间向量的加法法则.
[4] 通过本题深化对共线向量定理的理解,并能够运用共线向量定理证明.
[5] 此题深化向量共线定理,将其与端点共线建立关联,引导学生举一反三,加深理解,提高学生数学运算素养.
空间向量与立体几何
向量是具有大小和方向的量,这一概念既适用于平面,也适用于空间.空间向量的引入,为处理立体几何问题提供了新的视角,它是研究空间图形位置关系和度量问题的有力工具.本章我们在必修第二册“平面向量”的基础上,利用类比方法,学习空间向量的概念、运算(包括线性运算和数量积)、基本定理,并运用空间向量研究空间基本图形的平行、垂直等位置关系和距离、角度等度量问题.学习本章时应重视以下方面:第一,类比的方法.引导学生经历向量及其运算由平面向空间的推广过程.第二,直线的方向向量和平面的法向量的重要作用.第三,程序思想方法(即通性通法).通过用向量法求空间角和距离的解决过程,体会程序思想方法的优越性.
本章重点提升学生的直观想象、数学运算、逻辑推理素养.
6.1.1 空间向量的线性运算
知识技能
1. 了解空间向量及其线性运算由平面向空间推广的过程,掌握空间向量的线性运算及其性质.
2. 掌握空间向量共线的概念及定理.
思想方法
类比平面向量及其线性运算,尝试研究空间向量及其线性运算,建构空间向量及其线性运算的知识结构,发现并归纳它们的异同点.
核心素养
1. 将平面向量向空间推广的过程中,提升逻辑推理素养.
2. 在线性运算中提升数学运算素养.
教学重点:空间向量的概念、空间向量的线性运算及其运算律.
教学难点:空间向量的线性运算及其运算律.
问题导引
预习教材P5~7,思考下面的问题:
1. 什么是空间向量?如何表示空间向量?
2. 空间向量线性运算的运算法则和运算律有哪些?
3. 共线向量定理的内容是什么?
4. 空间向量与前面所学的平面向量有什么共性内容?
即时体验
1. (多选)下列等式中正确的是(ABD)
A. a+0=a
B. a+b=b+a
C. +=0
D. =++
2. 给出下列命题:
① 向量的长度与向量的长度相等;
② 若向量a与向量b平行,则a与b的方向相同或相反;
③ 两个有共同起点并且长度相等的向量的终点必相同;
④ 两个有共同终点的向量一定是共线向量;
⑤ 若向量与向量是共线向量,则A, B, C三点必在同一条直线上;
⑥ 有向线段就是向量,向量就是有向线段.
其中假命题有_4__个.
一、 问题情境
如图1,湖面上有三个景点O, A, B,一游艇将游客从景点O送至景点A,半小时后,游艇再将游客送至景点B.从景点O到景点A有一个位移,从景点A到景点B也有一个位移.
(图1)
问题1游客的位移与路程是否相同?(从大小与方向两方面考虑)
问题2游客的实际位移是什么?可以用什么数学概念来表示?
解 是向量,即+=.
(图2) (图3)
问题3如果游客还要到景点B下100m深处的海底世界D处游玩,游客实际发生的位移是什么?还是向量吗?它与上面的位移向量相同吗?为什么?
生:不同,因为O, A, B, D不在同一个平面内.
师:这就是我们今天要学习研究的内容——空间向量.(点题)
师:回忆一下平面向量的相关知识点,告诉我空间向量应该学习那些内容?用什么方法?
二、 数学建构
问题4空间向量与平面向量的相同点与不同点有哪些?[1]
1. 概念梳理
平面向量 空间向量
定义 既有大小又有方向的量
表示法 几何表示:―→ 字母表示:a,
向量的模 向量的大小
相同的向量 方向相同且大小相等的向量
相反向量 方向相反且大小相等的向量
单位向量 模长等于1的向量
2. 空间向量的线性运算(类比平面向量的线性运算)
(图4)
加法:a+b=+=;
减法:a-b=-=;
数乘:λa=(λ∈R).
3. 空间向量的运算律(类比平面向量的运算律)
(图5)
(1) 加法交换律:a+b=b+a;
(2) 加法结合律:(a+b)+c=a+(b+c);
(3) 数乘分配律:λ(a+b)=λa+λb(λ∈R).
4. 共线(平行)向量
(1) 定义:如果表示空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫作共线向量或平行向量.
记作:a ∥b.
规定:零向量与任意向量共线.
(2) 共线向量定理:对空间任意两个向量a, b(a≠0), b与a共线的充要条件是存在实数λ,使b=λa.
三、 数学运用
例1 (教材P6例1)如图,在三棱柱ABC A1B1C1中,M是BB1的中点.化简下列各式,并在图中标出化简得到的向量.
(例1)
(1) +; (2) ++;
(3) --.[2]
(见学生用书课堂本P1)
[处理建议] 运用向量加减法的三角形法则,若其中某个向量无法直接运用法则,则先将其化为适合法则的向量再运算.
[规范板书] 解 (1) +=.
(2) 因为M是BB1的中点,所以=.又=,所以++=+=.
(3) --=-=.
向量, , ,如图所示.
(1) ++…+An-1An=;
(2) ++…+An-1An+= 0 .
[题后反思] 注意:若有多个向量参与运算,按照“尾首相接,首尾相联”的原则进行运算.
例2 如图,在正方体ABCD A1B1C1D1中,点E是上底面A1B1C1D1的中心.若=m+n+,求m, n的值.[3]
(见学生用书课堂本P2)
(例2)
[处理建议] 引导学生将问题转化为向量如何用向量, , 表示,即可求得m, n的值.
[规范板书] 解 因为点E是上底面A1B1C1D1的中心,所以=(+)=(+)=+.又因为+=,所以m=n=.
在平行六面体ABCD A′B′C′D′中,若=x++,则x+y+z=_6__.
[规范板书] 解 在平行六面体ABCD A′B′C′D′中,=++,而=x++, 所以 得 所以x+y+z=6.
[题后反思] 逆向思维及转化思想是解决数学问题常用的方法.
例3 如图,在三棱锥A BCD中,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ∥平面BCD.[4]
(见学生用书课堂本P2)
(例3)
[处理建议] 利用空间向量共线的定义,证明线线平行及线面平行问题.
[规范板书] 证明 过点P, Q分别作PS∥AD交BD于点S, QT∥AD交CD于点T,连接ST,则=, =.因为=,所以=,所以四边形PQTS是平行四边形,则=.所以PQ∥ST.又因为PQ 平面BCD, ST 平面BCD,所以PQ∥平面BCD.
[题后反思] 将立体几何中的平行问题化归为向量共线问题,是解决立体几何中证明题的常用方法.
已知E, F, G, H分别为四面体ABCD的棱AB, BC, CD, DA的中点,且E, F, G, H四点共面,求证:BD∥平面EFGH.
(变式)
[规范板书] 证明 因为=-=-=,所以EH∥BD.又因为EH 平面EFGH, BD 平面EFGH,所以BD∥平面EFGH.
例4 设e1,e2是空间两个不共线的非零向量,已知=2e1+ke2, =e1+3e2, =2e1-e2,且A, B, D三点共线,求实数k的值.[5]
[处理建议] A, B, D三点共线即=λ,转化为向量共线问题进而求得k的值.
[规范板书] 解 =e1+3e2, =2e1-e2,故=+=(e1+3e2)+(-2e1+e2)=-e1+4e2. 因为A, B, D三点共线,所以=λ,即2e1+ke2=λ(-e1+4e2). 因为e1,e2是不共线的向量,所以 得k=-8.
[题后反思] 点共线问题可转化为向量共线问题来求解,再充分运用向量共线的充要条件“a=λb”和向量运算法则来解题.
已知e1, e2是空间两个不共线的非零向量,且=e1+ke2, =e1+3e2, =2e1-e2,若A, B, D三点共线,则k=-4.
四、 课堂练习
1. 化简:+++= 0 .
2. 在正方体ABCD A1B1C1D1中,下面化简后为零向量的是(A)
A. ++
B. -+
C. ++
D. +
3. (多选)已知正方体ABCD A1B1C1D1的中心为O,则下列结论正确的有(ACD)
A. +与+是一对相反向量
B. -与-是一对相反向量
C. +++与+++是一对相反向量
D. -与-是一对相反向量
4. 如图,在平行六面体ABCD A1B1C1D1中,G为△A1BD的重心.设=a, =b, =c,则=a+b+c.(用a, b, c表示)
(第4题)
提示 =+=+(+)=+(-)+(-)=++=a+b+c.
5. 如图,已知四边形ABCD与ABEF都是平行四边形且不共面,M, N分别是AC, BF的中点,判断与是否共线.
(第5题)
解 由题意知=++=++, =+++=-+--,两式相加得2=, 所以与共线.
五、 课堂小结
1. 空间向量的基本概念、线性运算及其运算律.
2. 运用类比的思想,掌握平面向量与空间向量的异同点.
[1] 阅读教材P5~6,要求学生通读一遍,精读一遍,复读一遍,然后完成下表.
[2] 此题主要是帮助学生熟悉空间向量的线性运算,熟练掌握运算法则,为后续学习奠定扎实的基础.
[3] 此题注重培养学生的转化思维方式,进一步巩固空间向量的加法法则.
[4] 通过本题深化对共线向量定理的理解,并能够运用共线向量定理证明.
[5] 此题深化向量共线定理,将其与端点共线建立关联,引导学生举一反三,加深理解,提高学生数学运算素养.
