北师大版数学九年级下册 3.2 圆的对称性 课件(共26张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 3.2 圆的对称性 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 314.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 00:00:00 | ||
图片预览


文档简介
(共26张PPT)
第3章 圆
3.2 圆的对称性
创设情境,引入新课
等腰三角形是轴对称图形吗?它的对称轴是什么?
什么是轴对称图形?
创设情境,引入新课
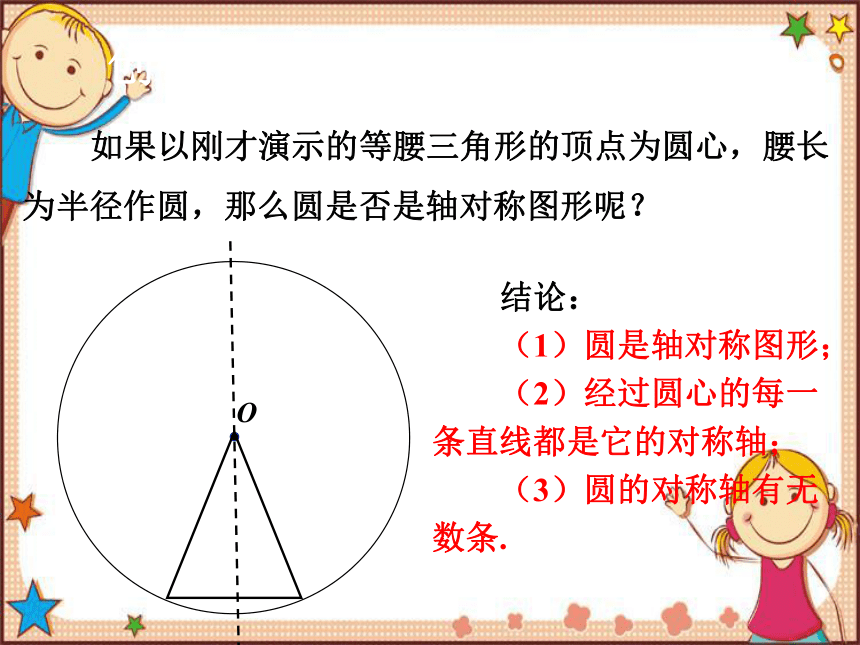
如果以刚才演示的等腰三角形的顶点为圆心,腰长为半径作圆,那么圆是否是轴对称图形呢?
O
结论:
(1)圆是轴对称图形;
(2)经过圆心的每一条直线都是它的对称轴;
(3)圆的对称轴有无数条.
创设情境,引入新课
平行四边形绕对角线交点O旋转180°后,结果怎样?这样的图形叫做什么图形?
O
创设情境,引入新课
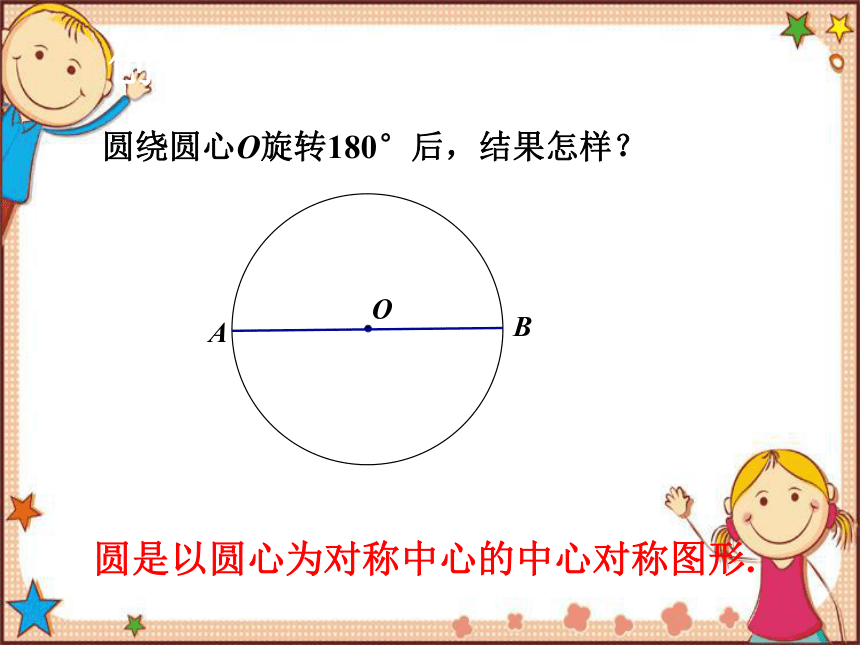
圆绕圆心O旋转180°后,结果怎样?
圆是以圆心为对称中心的中心对称图形.
O
A
B
创设情境,引入新课
圆绕圆心O旋转30°后,结果怎样?
O
A
B
创设情境,引入新课
圆绕圆心O旋转45°后,结果怎样?
O
A
B
创设情境,引入新课
圆绕圆心O旋转90°后,结果怎样?
不论圆绕圆心旋转多少度,都能够和原来的图形重合.
O
A
B
创设情境,引入新课
圆绕圆心O旋转任意角度α后,会发现什么?
圆的旋转不变性,即圆绕圆心旋转任意一个角度α,都能够与原来的图形重合.
O
A
B
创设情境,引入新课
圆心角:顶点在圆心上,角的两边与圆周相交的角叫做圆心角.如∠AOB.
弦心距:圆心到弦的垂线段的长度称为这条弦的弦心距.如线段OC.
概念:
O
A
B
C
探索新知
如图,先画一圆心角∠AOB,再画一圆心角∠A′OB′,如果∠AOB=∠A′OB′,作出它们所对的弦AB,A′B′和弦的弦心距OM,O′M′,请同学们大胆猜想,其余三组量 与 ,弦AB与A′B′,弦心距OM与OM′的大小关系如何?
AB=A′B′
OM=OM′
O
B′
A′
M′
A
B
M
探索新知
问题1:猜想是否正确,必须进行证明,怎样证明呢?
AB=A′B′ OM=OM′
O
B′
A′
M′
A
B
M
证明:因为圆的半径相等,且圆具有旋转不变性,又∠AOB=∠A′OB′ ,所以扇形AOB与扇形A′OB′ 旋转后能重合,点A与点A′重合,点B与点B′重合.
如何证明OM=OM′ ?
探索新知
问题2:既然等弧的定义是在同圆或等圆中,能够完全重合的弧叫等弧,那么用什么方法让弧重合呢?
O
B′
A′
M′
A
B
M
探索新知
圆心角、弧、弦、弦心距之间相等关系的定理:
在同圆或______中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
等圆
探索新知
已知⊙O与⊙O′为等圆,∠AOB=∠A′O′B′,OM与O′M′分别为AB与A′B′的弦心距,请回答:AB与A′B′,OM与O′M′还相等吗?为什么?
O
A
B
M
O′
A′
B′
M′
以上三组量仍然相等,因为两个等圆可以叠合成同圆.
探索新知
圆心角、弧、弦、弦心距之间相等关系的定理:
在同圆或______中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
等圆
为什么强调在“同圆或等圆中”呢?
O
A
B
C
D
探索新知
圆心角、弧、弦、弦心距之间相等关系的定理:
在同圆或______中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
等圆
条件:在同圆或等圆中,圆心角相等
结论:圆心角所对的弧相等;圆心角所对的弦相等;圆心角所对的弦的弦心距相等.
探索新知
定理是在同圆或等圆这个大前提下,已知圆心角相等,得出其余三组量相等,请同学们思考,在这个大前提下,把圆心角相等与三个结论中的任何一个交换位置,可以得到三个新命题,这三个命题是真命题吗?如何证明?
真命题
可利用旋转变换的思想证明
O
B′
A′
M′
A
B
M
探索新知
圆心角、弧、弦(弦心距)定理的推论:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦(两条弦的弦心距)中有一组量相等,那么它们所对应的其余各组量都分别相等.
利用它可以证明圆心角相等、弦相等、弧相等.一般可以通过三组量中的一组量相等来证明其他各组量相等.
巩固应用
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系? 与 的大小有什么关系?∠AOB与∠COD呢?为什么?
O
A
E
B
C
D
F
巩固应用
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
O
A
E
B
C
D
F
解:如果∠AOB=∠COD,那么OE=OF.
理由是:∵∠AOB=∠COD,∴AB=CD.
∵OE⊥AB,OF⊥CD,∴AE= AB,CF= CD. ∴AE=CF.
又∵OA=OC,∴Rt△OAE≌Rt△OCF.
∴OE=OF.
巩固应用
O
A
E
B
C
D
F
解:如果OE=OF,那么AB=CD,AB=CD,∠AOB=∠COD.
理由是:∵OA=OC,OE=OF, ∴Rt △OAE≌Rt△OCF.
∴AE=CF.
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(2)如果OE=OF,那么AB与CD的大小有什么关系? 与 的大小有什么关系?∠AOB与∠COD呢?为什么?
又∵OE⊥AB,OF⊥CD,∴AE= AB,CF= CD.
∴AB=2AE,CD=2CF.
∴AB=CD,AB=CD,∠AOB=∠COD.
1.这节课主要学习了两部分内容:一是证明了圆既是轴对称图形,也是中心对称图形,得到圆的特性——圆的旋转不变性;二是学习了在同圆或等圆中,圆心角、圆心角所对的弧、所对的弦、所对的弦的弦心距之间的关系定理及推论.这些内容是我们今后证明弧相等、弦相等、角相等的重要依据.
课堂小结
2.本节通过观察—猜想—论证的方法,从运动变化中发现规律,得出定理及推论,同时遵循由特殊到一般的思维认识规律,渗透了旋转交换的思想.
3.在运用定理及推论解题时,必须注意要有“在同圆或等圆中”这一前提条件.
课堂小结
教材第72~73页习题3.2第1,3题.
布置作业
谢谢大家!
再见!
第3章 圆
3.2 圆的对称性
创设情境,引入新课
等腰三角形是轴对称图形吗?它的对称轴是什么?
什么是轴对称图形?
创设情境,引入新课
如果以刚才演示的等腰三角形的顶点为圆心,腰长为半径作圆,那么圆是否是轴对称图形呢?
O
结论:
(1)圆是轴对称图形;
(2)经过圆心的每一条直线都是它的对称轴;
(3)圆的对称轴有无数条.
创设情境,引入新课
平行四边形绕对角线交点O旋转180°后,结果怎样?这样的图形叫做什么图形?
O
创设情境,引入新课
圆绕圆心O旋转180°后,结果怎样?
圆是以圆心为对称中心的中心对称图形.
O
A
B
创设情境,引入新课
圆绕圆心O旋转30°后,结果怎样?
O
A
B
创设情境,引入新课
圆绕圆心O旋转45°后,结果怎样?
O
A
B
创设情境,引入新课
圆绕圆心O旋转90°后,结果怎样?
不论圆绕圆心旋转多少度,都能够和原来的图形重合.
O
A
B
创设情境,引入新课
圆绕圆心O旋转任意角度α后,会发现什么?
圆的旋转不变性,即圆绕圆心旋转任意一个角度α,都能够与原来的图形重合.
O
A
B
创设情境,引入新课
圆心角:顶点在圆心上,角的两边与圆周相交的角叫做圆心角.如∠AOB.
弦心距:圆心到弦的垂线段的长度称为这条弦的弦心距.如线段OC.
概念:
O
A
B
C
探索新知
如图,先画一圆心角∠AOB,再画一圆心角∠A′OB′,如果∠AOB=∠A′OB′,作出它们所对的弦AB,A′B′和弦的弦心距OM,O′M′,请同学们大胆猜想,其余三组量 与 ,弦AB与A′B′,弦心距OM与OM′的大小关系如何?
AB=A′B′
OM=OM′
O
B′
A′
M′
A
B
M
探索新知
问题1:猜想是否正确,必须进行证明,怎样证明呢?
AB=A′B′ OM=OM′
O
B′
A′
M′
A
B
M
证明:因为圆的半径相等,且圆具有旋转不变性,又∠AOB=∠A′OB′ ,所以扇形AOB与扇形A′OB′ 旋转后能重合,点A与点A′重合,点B与点B′重合.
如何证明OM=OM′ ?
探索新知
问题2:既然等弧的定义是在同圆或等圆中,能够完全重合的弧叫等弧,那么用什么方法让弧重合呢?
O
B′
A′
M′
A
B
M
探索新知
圆心角、弧、弦、弦心距之间相等关系的定理:
在同圆或______中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
等圆
探索新知
已知⊙O与⊙O′为等圆,∠AOB=∠A′O′B′,OM与O′M′分别为AB与A′B′的弦心距,请回答:AB与A′B′,OM与O′M′还相等吗?为什么?
O
A
B
M
O′
A′
B′
M′
以上三组量仍然相等,因为两个等圆可以叠合成同圆.
探索新知
圆心角、弧、弦、弦心距之间相等关系的定理:
在同圆或______中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
等圆
为什么强调在“同圆或等圆中”呢?
O
A
B
C
D
探索新知
圆心角、弧、弦、弦心距之间相等关系的定理:
在同圆或______中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
等圆
条件:在同圆或等圆中,圆心角相等
结论:圆心角所对的弧相等;圆心角所对的弦相等;圆心角所对的弦的弦心距相等.
探索新知
定理是在同圆或等圆这个大前提下,已知圆心角相等,得出其余三组量相等,请同学们思考,在这个大前提下,把圆心角相等与三个结论中的任何一个交换位置,可以得到三个新命题,这三个命题是真命题吗?如何证明?
真命题
可利用旋转变换的思想证明
O
B′
A′
M′
A
B
M
探索新知
圆心角、弧、弦(弦心距)定理的推论:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦(两条弦的弦心距)中有一组量相等,那么它们所对应的其余各组量都分别相等.
利用它可以证明圆心角相等、弦相等、弧相等.一般可以通过三组量中的一组量相等来证明其他各组量相等.
巩固应用
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系? 与 的大小有什么关系?∠AOB与∠COD呢?为什么?
O
A
E
B
C
D
F
巩固应用
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
O
A
E
B
C
D
F
解:如果∠AOB=∠COD,那么OE=OF.
理由是:∵∠AOB=∠COD,∴AB=CD.
∵OE⊥AB,OF⊥CD,∴AE= AB,CF= CD. ∴AE=CF.
又∵OA=OC,∴Rt△OAE≌Rt△OCF.
∴OE=OF.
巩固应用
O
A
E
B
C
D
F
解:如果OE=OF,那么AB=CD,AB=CD,∠AOB=∠COD.
理由是:∵OA=OC,OE=OF, ∴Rt △OAE≌Rt△OCF.
∴AE=CF.
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(2)如果OE=OF,那么AB与CD的大小有什么关系? 与 的大小有什么关系?∠AOB与∠COD呢?为什么?
又∵OE⊥AB,OF⊥CD,∴AE= AB,CF= CD.
∴AB=2AE,CD=2CF.
∴AB=CD,AB=CD,∠AOB=∠COD.
1.这节课主要学习了两部分内容:一是证明了圆既是轴对称图形,也是中心对称图形,得到圆的特性——圆的旋转不变性;二是学习了在同圆或等圆中,圆心角、圆心角所对的弧、所对的弦、所对的弦的弦心距之间的关系定理及推论.这些内容是我们今后证明弧相等、弦相等、角相等的重要依据.
课堂小结
2.本节通过观察—猜想—论证的方法,从运动变化中发现规律,得出定理及推论,同时遵循由特殊到一般的思维认识规律,渗透了旋转交换的思想.
3.在运用定理及推论解题时,必须注意要有“在同圆或等圆中”这一前提条件.
课堂小结
教材第72~73页习题3.2第1,3题.
布置作业
谢谢大家!
再见!
