北师大版数学九年级下册 1.2 30°,45°,60°角的三角函数值 课件(共25张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 1.2 30°,45°,60°角的三角函数值 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 749.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 10:39:31 | ||
图片预览






文档简介
(共25张PPT)
第1章 直角三角形的边角关系
1.2 30°,45°,60°角的三角函数值
如图,为了测量一棵大树的高度,准备了如下测量工具:①含30°和60°两个锐角的三角尺;②皮尺.
创设问题情境,引入新课
请你设计一个测量方案,测出这棵大树的高度.
如图,让一位同学拿着三角尺站在一个适当的位置B处,使这位同学拿起三角尺,她的视线恰好和斜边重合且过树梢C点,30°角的邻边和水平方向平行,用卷尺测出AB的长度、BE的长度,
因为DE=AB ,所以只需在
Rt△CDA中求出CD的
长度即可.
创设问题情境,引入新课
B
A
C
D
E
在Rt△CDA中,∠ CAD =30°,AD =BE, BE是已知的,设BE =a米,则AD=a米.
创设问题情境,引入新课
B
A
C
D
E
含30°角的直角三角形有一个非常重要的性质: 30°的角所对的直角边等于斜边的一半,即AC =2CD.
根据勾股定理,得(2CD)2=CD2+a2,
所以
树高CE=DE+CD.
我们前面学习了三角函数的定义,如果一个角的大小确定,那么它的正切、正弦、余弦值也随之确定,如果能求出30°角的正切值,在上图中,
你能求出30°角的三角函数值吗?
创设问题情境,引入新课
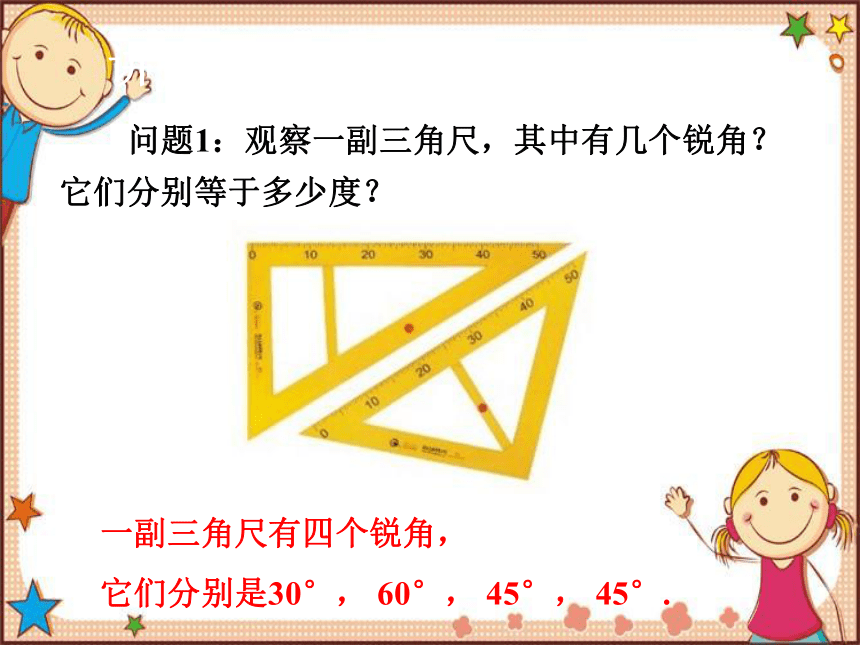
问题1:观察一副三角尺,其中有几个锐角?它们分别等于多少度?
讲授新课
一副三角尺有四个锐角,
它们分别是30°, 60°, 45°, 45°.
问题2:sin 30°等于多少呢?你是怎样得到的?与同伴交流.
讲授新课
不妨设30°角所对的边为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,知斜边等于2a.根据勾股定理,可知30°角的邻边为 ,所以
30°
60°
2a
a
sin 30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.
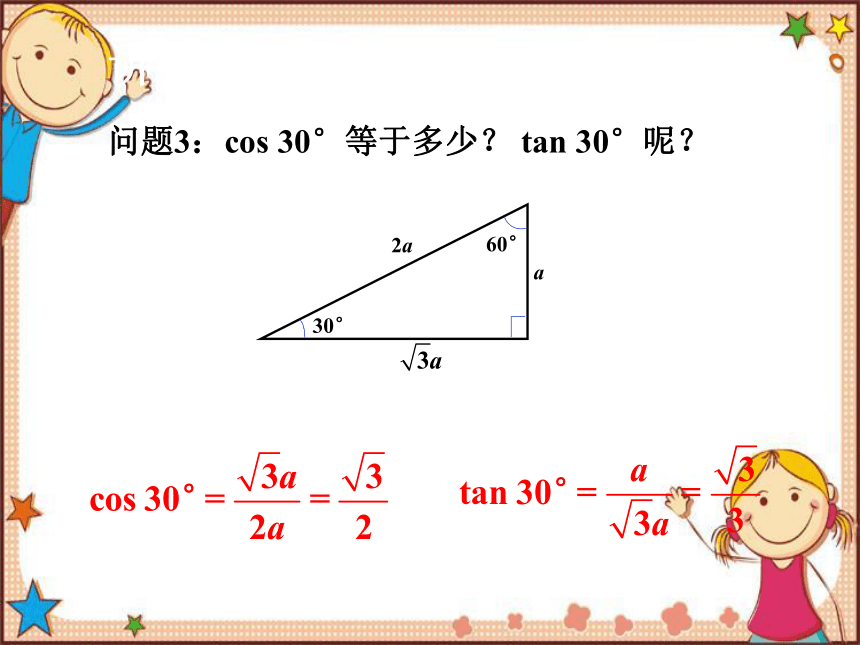
问题3:cos 30°等于多少? tan 30°呢?
讲授新课
30°
60°
2a
a
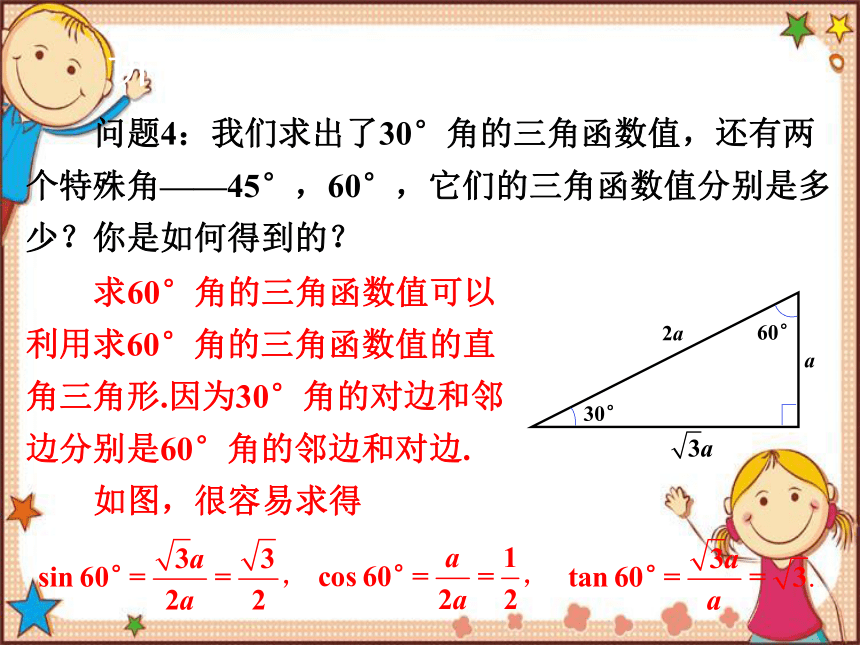
问题4:我们求出了30°角的三角函数值,还有两个特殊角——45°,60°,它们的三角函数值分别是多少?你是如何得到的?
讲授新课
求60°角的三角函数值可以利用求60°角的三角函数值的直角三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.
如图,很容易求得
30°
60°
2a
a
问题4:我们求出了30°角的三角函数值,还有两个特殊角——45°,60°,它们的三角函数值分别是多少?你是如何得到的?
讲授新课
也可以利用上节课我们得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知
30°
60°
2a
a
探究45°角的三角函数值:
含45°角的直角三角形是等腰直角三角形(如图).
讲授新课
设其中一条直角边为a,则斜边为 .由此可求得
45°
a
a
讲授新课
30° , 45° ,60°角的三角函数值
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
讲授新课
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
探究:(1)第一列30°,45°,60°角的正弦值,你能发现什么规律?
显然30°,45°,60°角的正弦值的分母都为2,分子从小到大分别为 ,随着角度的增大,正弦值在逐渐增大.
讲授新课
探究:(2)第二列三角函数值,有何特点呢?
显然第二列是30°,45°,60°角的余弦值,它们的分母也都为2,而分子从大到小分别为 ,余弦值随角度的增大而减小.
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
讲授新课
探究:(3)第三列呢?
显然第三列是30°,45°,60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan 45°=1比较特殊.但通过比较可以得出,正切值随角度的增大而增大.
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
讲授新课
你掌握这些规律了吗?互相检查一下你对30° , 45° ,60°角的三角函数值的记忆情况吧!
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
例1.计算:
(1)sin 30°+cos 45°;
(2)sin260°+cos260°-tan 45°.
例题讲解
例2.一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好是60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01 m).
例题讲解
B
D
O
A
C
例2.一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好是60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01 m).
例题讲解
B
D
O
A
C
解:根据题意可知,∠BOD=60°,OB=OA=OD=2.5 m, ∠AOD=30°,
∴OC=ODcos 30 °=
∴AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度之差约为0.34 m.
1.计算:
(1)sin 60°-tan 45°;
(2)cos 60°+tan 60°;
(3) sin 45°+sin 60°-2cos 45°.
随堂练习
2.某商场有一自动扶梯,其倾斜角为30°,高为7 m.扶梯的长度是多少?
14 m
随堂练习
A
B
C
7
30°
1.探索30° , 45° ,60°角的三角函数值.
课堂小结
2.能进行含30° , 45° ,60°角的三角函数值的计算.
3.能根据30° , 45° ,60°角的三角函数值,说出相应锐角的大小.
课堂小结
教材第10页习题1.3第1~4题.
课后作业
谢谢大家!
再见!
第1章 直角三角形的边角关系
1.2 30°,45°,60°角的三角函数值
如图,为了测量一棵大树的高度,准备了如下测量工具:①含30°和60°两个锐角的三角尺;②皮尺.
创设问题情境,引入新课
请你设计一个测量方案,测出这棵大树的高度.
如图,让一位同学拿着三角尺站在一个适当的位置B处,使这位同学拿起三角尺,她的视线恰好和斜边重合且过树梢C点,30°角的邻边和水平方向平行,用卷尺测出AB的长度、BE的长度,
因为DE=AB ,所以只需在
Rt△CDA中求出CD的
长度即可.
创设问题情境,引入新课
B
A
C
D
E
在Rt△CDA中,∠ CAD =30°,AD =BE, BE是已知的,设BE =a米,则AD=a米.
创设问题情境,引入新课
B
A
C
D
E
含30°角的直角三角形有一个非常重要的性质: 30°的角所对的直角边等于斜边的一半,即AC =2CD.
根据勾股定理,得(2CD)2=CD2+a2,
所以
树高CE=DE+CD.
我们前面学习了三角函数的定义,如果一个角的大小确定,那么它的正切、正弦、余弦值也随之确定,如果能求出30°角的正切值,在上图中,
你能求出30°角的三角函数值吗?
创设问题情境,引入新课
问题1:观察一副三角尺,其中有几个锐角?它们分别等于多少度?
讲授新课
一副三角尺有四个锐角,
它们分别是30°, 60°, 45°, 45°.
问题2:sin 30°等于多少呢?你是怎样得到的?与同伴交流.
讲授新课
不妨设30°角所对的边为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,知斜边等于2a.根据勾股定理,可知30°角的邻边为 ,所以
30°
60°
2a
a
sin 30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.
问题3:cos 30°等于多少? tan 30°呢?
讲授新课
30°
60°
2a
a
问题4:我们求出了30°角的三角函数值,还有两个特殊角——45°,60°,它们的三角函数值分别是多少?你是如何得到的?
讲授新课
求60°角的三角函数值可以利用求60°角的三角函数值的直角三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.
如图,很容易求得
30°
60°
2a
a
问题4:我们求出了30°角的三角函数值,还有两个特殊角——45°,60°,它们的三角函数值分别是多少?你是如何得到的?
讲授新课
也可以利用上节课我们得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知
30°
60°
2a
a
探究45°角的三角函数值:
含45°角的直角三角形是等腰直角三角形(如图).
讲授新课
设其中一条直角边为a,则斜边为 .由此可求得
45°
a
a
讲授新课
30° , 45° ,60°角的三角函数值
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
讲授新课
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
探究:(1)第一列30°,45°,60°角的正弦值,你能发现什么规律?
显然30°,45°,60°角的正弦值的分母都为2,分子从小到大分别为 ,随着角度的增大,正弦值在逐渐增大.
讲授新课
探究:(2)第二列三角函数值,有何特点呢?
显然第二列是30°,45°,60°角的余弦值,它们的分母也都为2,而分子从大到小分别为 ,余弦值随角度的增大而减小.
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
讲授新课
探究:(3)第三列呢?
显然第三列是30°,45°,60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan 45°=1比较特殊.但通过比较可以得出,正切值随角度的增大而增大.
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
讲授新课
你掌握这些规律了吗?互相检查一下你对30° , 45° ,60°角的三角函数值的记忆情况吧!
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
例1.计算:
(1)sin 30°+cos 45°;
(2)sin260°+cos260°-tan 45°.
例题讲解
例2.一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好是60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01 m).
例题讲解
B
D
O
A
C
例2.一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好是60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01 m).
例题讲解
B
D
O
A
C
解:根据题意可知,∠BOD=60°,OB=OA=OD=2.5 m, ∠AOD=30°,
∴OC=ODcos 30 °=
∴AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度之差约为0.34 m.
1.计算:
(1)sin 60°-tan 45°;
(2)cos 60°+tan 60°;
(3) sin 45°+sin 60°-2cos 45°.
随堂练习
2.某商场有一自动扶梯,其倾斜角为30°,高为7 m.扶梯的长度是多少?
14 m
随堂练习
A
B
C
7
30°
1.探索30° , 45° ,60°角的三角函数值.
课堂小结
2.能进行含30° , 45° ,60°角的三角函数值的计算.
3.能根据30° , 45° ,60°角的三角函数值,说出相应锐角的大小.
课堂小结
教材第10页习题1.3第1~4题.
课后作业
谢谢大家!
再见!
