人教版数学八年级下册 17.1 勾股定理第2课时 勾股定理的应用 课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级下册 17.1 勾股定理第2课时 勾股定理的应用 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 332.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 10:47:26 | ||
图片预览






文档简介
(共17张PPT)
17.1 勾股定理
第17章 勾股定理
第2课时 勾股定理的应用
复习引入
1.勾股定理的内容:
________________________________________
________________________________________
如果直角三角形的两条直角边长分别为a,b,
斜边长为c,那么a2+b2=c2.
复习引入
2.在Rt△ABC中, a,b,c分别是∠A, ∠B ,∠C的对边,则
(1)c= ;
(2)a= ;
(3)b= .
3.锐角三角形、钝角三角形是否满足勾股定理?
∠C=90°,
不满足
解决问题
探究一:利用勾股定理证明HL定理
(1)回忆HL定理的内容.
斜边和一条直角边对应相等的两个直角三角形全等.
解决问题
探究一:利用勾股定理证明HL定理
(2)写出已知、求证、证明.
已知:如图,在Rt△ABC和Rt△A B C 中,∠C=∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
解决问题
证明:在Rt△ABC和Rt △A B C 中,
∠C= ∠C =90°,根据勾股定理,得
BC=
又AB=A B ,AC= A C ,
∴ BC= B C .
∴ △ABC≌△A B C .
解决问题
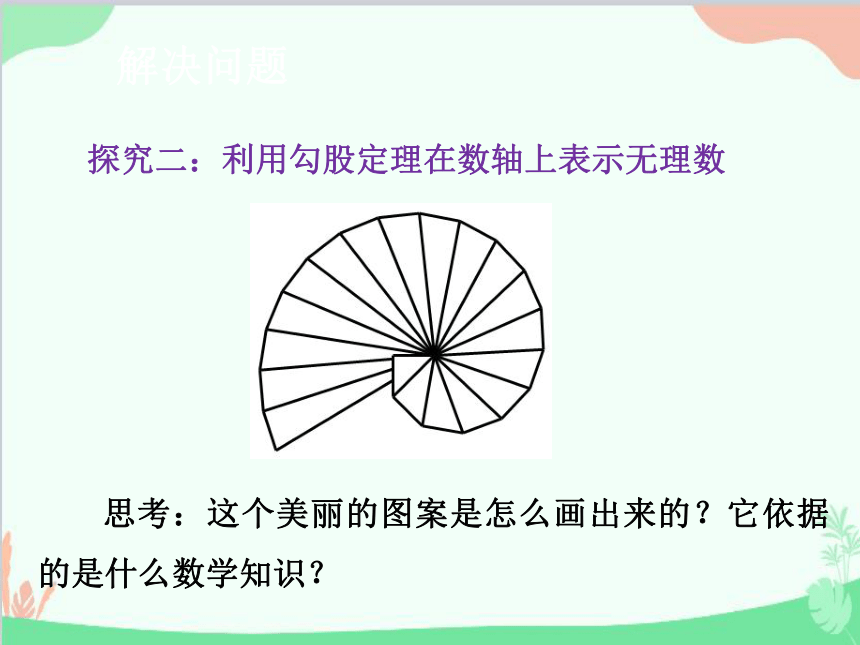
探究二:利用勾股定理在数轴上表示无理数
思考:这个美丽的图案是怎么画出来的?它依据的是什么数学知识?
观察发现:
图形由若干个直角三角形构成,是根据我们所学的勾股定理来完成的.
解决问题
解决问题
我们知道 是边长为1的等腰直角三角形的斜边的长,可是在数轴上如何表示出 呢 如何表示
呢?
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
解决问题
你能在数轴上画出表示 的点吗?
提示:要在数轴上画出表示 的点,只要画出长为 的线段.利用勾股定理,则有
解决问题
你能在数轴上画出表示 的点吗?
画法:设原点为O,在数轴正半轴上找到点A,使OA=3,过点A作直线l垂直于OA,在l上取一点B,使AB=2,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
巩固练习
1.在数轴上作出表示 的点.
作法:设原点为O,在数轴正半轴上找到点A,使OA=4,过点A作直线l垂直于OA,在l上取一点B,使AB=1,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
巩固练习
2.在数轴上画出表示 的点.
课堂小结
1.勾股定理在证明时的应用.
2.利用勾股定理在数轴上表示无理数的方法.
布置作业
思考题:
如何在数轴上画出表示 的点?
必做题:
教材第28~29页习题17.1第6,9,10题.
谢谢 !
17.1 勾股定理
第17章 勾股定理
第2课时 勾股定理的应用
复习引入
1.勾股定理的内容:
________________________________________
________________________________________
如果直角三角形的两条直角边长分别为a,b,
斜边长为c,那么a2+b2=c2.
复习引入
2.在Rt△ABC中, a,b,c分别是∠A, ∠B ,∠C的对边,则
(1)c= ;
(2)a= ;
(3)b= .
3.锐角三角形、钝角三角形是否满足勾股定理?
∠C=90°,
不满足
解决问题
探究一:利用勾股定理证明HL定理
(1)回忆HL定理的内容.
斜边和一条直角边对应相等的两个直角三角形全等.
解决问题
探究一:利用勾股定理证明HL定理
(2)写出已知、求证、证明.
已知:如图,在Rt△ABC和Rt△A B C 中,∠C=∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
解决问题
证明:在Rt△ABC和Rt △A B C 中,
∠C= ∠C =90°,根据勾股定理,得
BC=
又AB=A B ,AC= A C ,
∴ BC= B C .
∴ △ABC≌△A B C .
解决问题
探究二:利用勾股定理在数轴上表示无理数
思考:这个美丽的图案是怎么画出来的?它依据的是什么数学知识?
观察发现:
图形由若干个直角三角形构成,是根据我们所学的勾股定理来完成的.
解决问题
解决问题
我们知道 是边长为1的等腰直角三角形的斜边的长,可是在数轴上如何表示出 呢 如何表示
呢?
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
解决问题
你能在数轴上画出表示 的点吗?
提示:要在数轴上画出表示 的点,只要画出长为 的线段.利用勾股定理,则有
解决问题
你能在数轴上画出表示 的点吗?
画法:设原点为O,在数轴正半轴上找到点A,使OA=3,过点A作直线l垂直于OA,在l上取一点B,使AB=2,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
巩固练习
1.在数轴上作出表示 的点.
作法:设原点为O,在数轴正半轴上找到点A,使OA=4,过点A作直线l垂直于OA,在l上取一点B,使AB=1,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
巩固练习
2.在数轴上画出表示 的点.
课堂小结
1.勾股定理在证明时的应用.
2.利用勾股定理在数轴上表示无理数的方法.
布置作业
思考题:
如何在数轴上画出表示 的点?
必做题:
教材第28~29页习题17.1第6,9,10题.
谢谢 !
