1.3.1函数的单调性(1)[上学期]
文档属性
| 名称 | 1.3.1函数的单调性(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 276.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-16 00:00:00 | ||
图片预览

文档简介
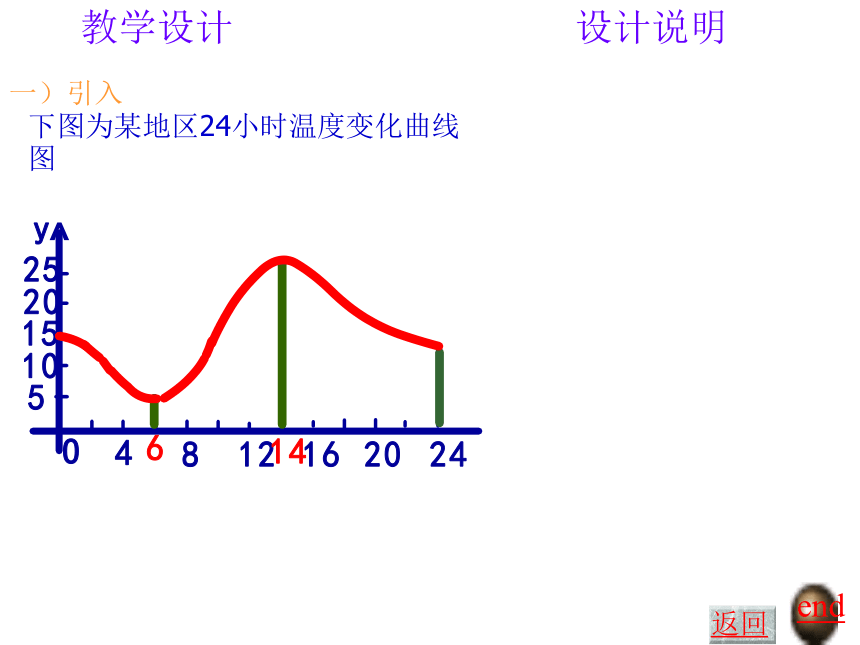
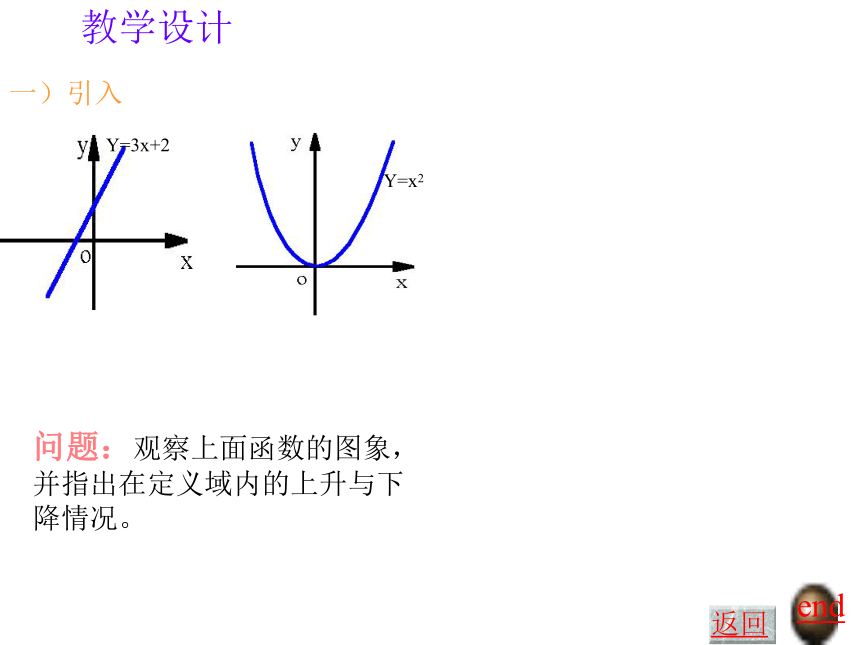
课件18张PPT。函数的单调性教学设计设计说明一)引入end返回下图为某地区24小时温度变化曲线图教学设计一)引入问题:观察上面函数的图象,并指出在定义域内的上升与下降情况。Y=3x+2Y=x2end返回[m,n]上,函数
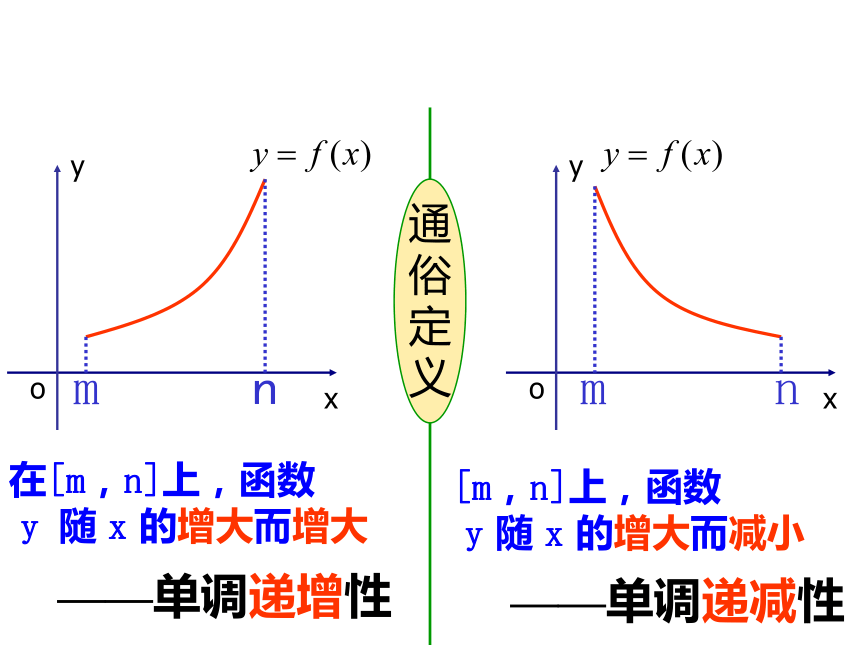
y 随 x 的增大而减小在[m,n]上,函数
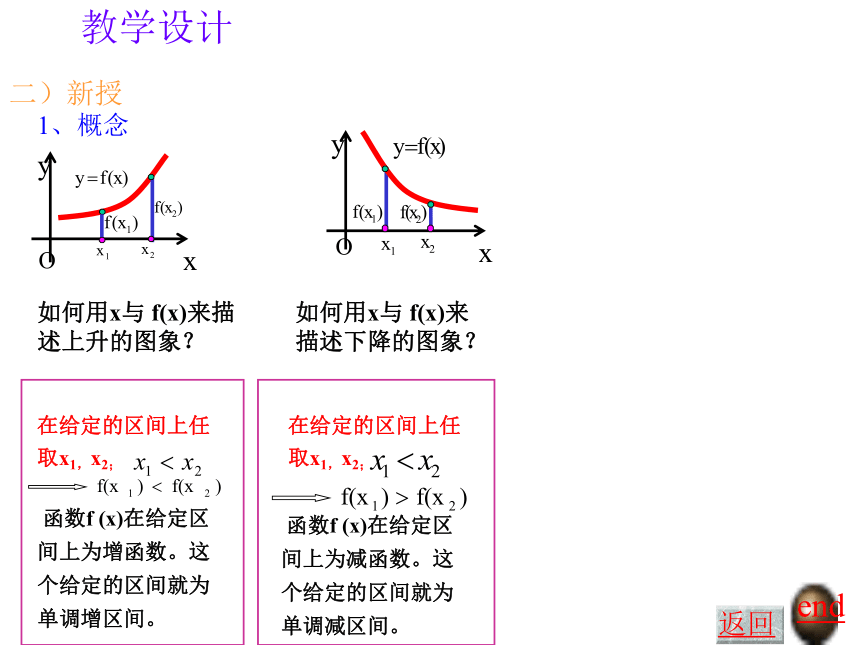
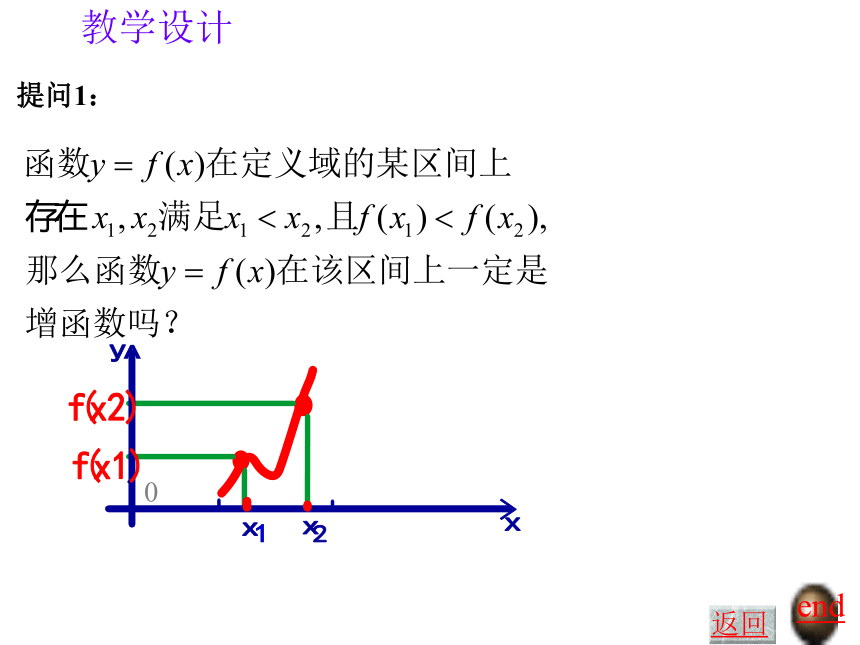
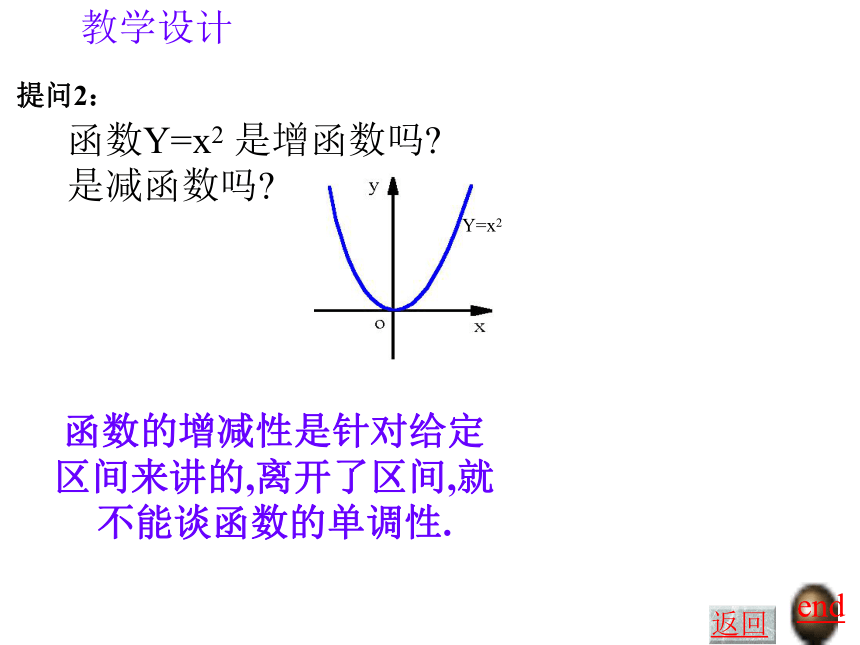
y 随 x 的增大而增大——单调递增性——单调递减性教学设计二)新授如何用x与 f(x)来描述上升的图象?如何用x与 f(x)来描述下降的图象?end返回1、概念教学设计 提问1:end返回0教学设计 提问2:end返回Y=x2函数Y=x2 是增函数吗?
是减函数吗?函数的增减性是针对给定区间来讲的,离开了区间,就不能谈函数的单调性.教学设计2、判定(证明)方法(1)图象法: 从左向右看图象的升降情况 例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。end返回解答教学设计讨论一次函数的单调性end返回结论:(2)二次函数单调性(3)反比例函数的单调性教学设计(2)定义法:利用定义判定(证明)函数的增、减性例2:证明函数f(x)=3x+2在
R上是增函数。end返回解答教学设计例3 证明函数f(x)=1/x 在
(0,+∞)上是减函数。解答end返回例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。在区间[-2,1), [3, 5]上是增函数。答:函数y=f(x)的单调区间有[-5,-2),[-2,1), [1,3), [3,5], 其中 y=f(x)在区间[-5, -2), [1,3)上是减函数,end返回例2:证明函数f(x)=3x+2在R上是增函数。 f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)由x1即 f(x1)取值定号变形作差判断end返回end返回例3、证明函数f(x)=1/x 在(0,+∞)上是减函数。 证明:设x1,x2是(0,+∞)上任意两个实数,且x1 则 f(x1)- f(x2)=由于x1,x2 得x1x2>0又由x10
所以f(x1)- f(x2)>0
即f(x1)> f(x2)
所以f(x)=1/x 在(0,+∞)上是减函数。小结
1.讨论函数的单调性必须在定义域内进行,即函数的单调区间是其定义域的子集.因此讨论函数的单调性,必须先确定函数的定义域;
2.函数的单调性是针对给定区间而言的.
3.根据定义证明函数单调性的一般步骤是:
(1)取值 且x1(2)作差 f(x1)-f(x2);并将此差式变形(要注意变形的程度);
(3)判断f(x1)-f(x2)的正负(要注意说理的充分性);(定号)
(4)下结论要求: ①会根据图象判断函数的
单调性. ②会根据定义证明函数的
单调性.返回
y 随 x 的增大而减小在[m,n]上,函数
y 随 x 的增大而增大——单调递增性——单调递减性教学设计二)新授如何用x与 f(x)来描述上升的图象?如何用x与 f(x)来描述下降的图象?end返回1、概念教学设计 提问1:end返回0教学设计 提问2:end返回Y=x2函数Y=x2 是增函数吗?
是减函数吗?函数的增减性是针对给定区间来讲的,离开了区间,就不能谈函数的单调性.教学设计2、判定(证明)方法(1)图象法: 从左向右看图象的升降情况 例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。end返回解答教学设计讨论一次函数的单调性end返回结论:(2)二次函数单调性(3)反比例函数的单调性教学设计(2)定义法:利用定义判定(证明)函数的增、减性例2:证明函数f(x)=3x+2在
R上是增函数。end返回解答教学设计例3 证明函数f(x)=1/x 在
(0,+∞)上是减函数。解答end返回例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。在区间[-2,1), [3, 5]上是增函数。答:函数y=f(x)的单调区间有[-5,-2),[-2,1), [1,3), [3,5], 其中 y=f(x)在区间[-5, -2), [1,3)上是减函数,end返回例2:证明函数f(x)=3x+2在R上是增函数。 f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)由x1
所以f(x1)- f(x2)>0
即f(x1)> f(x2)
所以f(x)=1/x 在(0,+∞)上是减函数。小结
1.讨论函数的单调性必须在定义域内进行,即函数的单调区间是其定义域的子集.因此讨论函数的单调性,必须先确定函数的定义域;
2.函数的单调性是针对给定区间而言的.
3.根据定义证明函数单调性的一般步骤是:
(1)取值 且x1
(3)判断f(x1)-f(x2)的正负(要注意说理的充分性);(定号)
(4)下结论要求: ①会根据图象判断函数的
单调性. ②会根据定义证明函数的
单调性.返回
