人教版八年级下册 17.1 勾股定理(第3课时)课件(共24张PPT)
文档属性
| 名称 | 人教版八年级下册 17.1 勾股定理(第3课时)课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 543.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 11:59:44 | ||
图片预览







文档简介
(共24张PPT)
17.1 勾股定理
第十七章 勾股定理
第3课时 利用勾股定理作图或计算
1.可以运用勾股定理处理几何中的问题.
2.可以运用勾股定理进行计算.
重点难点:
1.会运用勾股定理确定数轴上表示实数的点及解决网格问题.
2.灵活运用勾股定理进行计算,并会运用勾股定理解决相应的折叠问题.
学习目标:
情景导入
某拍卖行贴出了如下的一个土地拍卖广告:如下图,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩、116英亩、370英亩.三个正方形恰好围着一个池塘,如果有人能计算出池塘的准确面积.则池塘不计入土地价钱白白奉送.英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗
知识精讲
知识点一 用勾股定理在数轴上表示数
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都为1的直角三角形的斜边.长为 的线段能是直角边的长为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,直角边的长为正整数2, 3的直角三角形的斜边长为 .由此,可以依照如下方法在数轴上画出表示 的点.
如图,在数轴上找出表示3的点A, 则OA =3,过点A作直
线l 垂直于OA,在l上取点B,使AB = 2,以原点O为圆心,以
OB为半径作弧,弧与数轴的交点C即为表示 的点.
0
1
2
3
4
l
A
B
C
O
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边长为1和2,
∴斜边长为 ,即-1到A的距离是 ,
∴点A所表示的数为 .
注意:求点表示的数时注意画弧的起点不从原点起,则所表示的数不是斜边长.
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
归纳:
针对练习
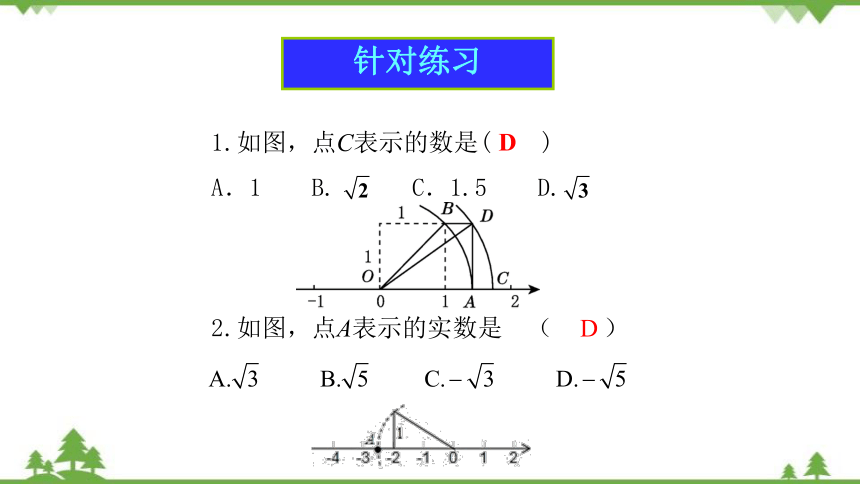
1.如图,点C表示的数是( )
A.1 B. C.1.5 D.
D
2.如图,点A表示的实数是 ( )
D
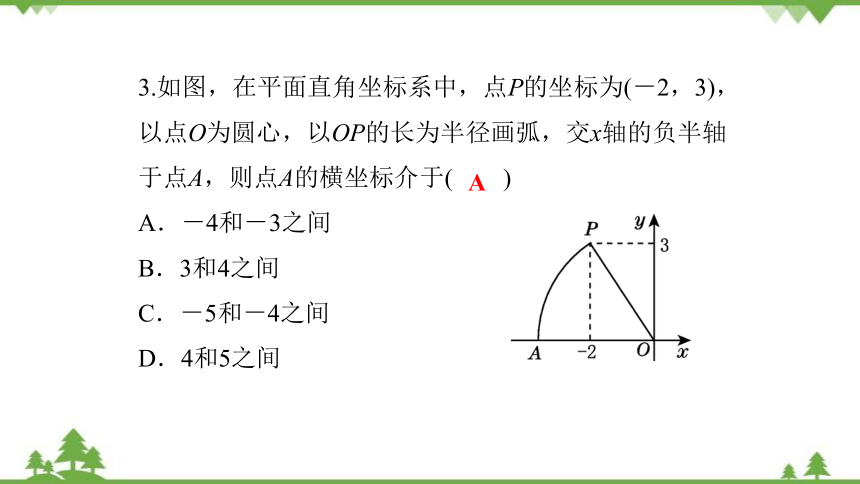
3.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
A
知识点二 勾股定理在网格中的应用
例2 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).由勾股定理得
∴△ABC的周长为
归纳:勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
例3 如图,在2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,求AB边上的高.
解:如图,过点C作CD⊥AB于点D.
D
归纳:此类网格中求格点三角形的高的题,常用的方法是利用网格求面积,再用面积法求高.
针对练习
1.如图,在5×5的正方形网格中,每个小正方形的边长均为1,画出一个三角形的长分别为 .
A
B
C
解:如图所示.
2.如图,每个小正方形的边长均为1,则△ABC中,长为无理数的边有( )
A.0条
B.1条
C.2条
D.3条
C
知识点三 勾股定理在几何问题中的应用
例4 如图,在△ABC中,∠C=60°,AB=14,AC=10. 求BC的长.
解:如图,过点A作AD⊥BC于D.
∵∠ADC=90°,∠C=60°,
∴CD= ,AC=5.
在Rt△ACD中,AD
在Rt△ABD中,BD
∴BC=BD+CD=11+5=16.
例5 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,解得 x=3.
D
A
B
C
E
F
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线数或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
归纳:
针对练习
1.如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm
B.5 cm
C.6 cm
D.10 cm
B
2.如图,在等腰三角形ABC中,AB=AC,BC边上的高AD=6 cm,腰AB上的高CE=8 cm,则△ABC的周长等于________cm.
当堂检测
1.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
2.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
A.3
B.
C.5
D.
C
3.如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段________条.
8
4.如图,网格中的小正方形边长均为1,△ABC的三个顶点均在格点上,则AB边上的高为_______.
5.如图,等边三角形的边长是6.求:
(1)高AD的长;
(2)这个三角形的面积.
解:(1)由题意可知,在Rt△ADB中,
AB=6,BD= BC=3,∠ADB=90°.
由勾股定理,得AD=
(2)S△ABC= BC·AD= ×6×3
=
6.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿 AC折叠,点D落在点D′处,求重叠部分△AFC的面积.
解:易证△AFD′≌△CFB∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,
解得x=3.∴AF=AB-FB=8-3=5,
∴S△AFC= AF BC=10.
课堂小结
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
17.1 勾股定理
第十七章 勾股定理
第3课时 利用勾股定理作图或计算
1.可以运用勾股定理处理几何中的问题.
2.可以运用勾股定理进行计算.
重点难点:
1.会运用勾股定理确定数轴上表示实数的点及解决网格问题.
2.灵活运用勾股定理进行计算,并会运用勾股定理解决相应的折叠问题.
学习目标:
情景导入
某拍卖行贴出了如下的一个土地拍卖广告:如下图,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩、116英亩、370英亩.三个正方形恰好围着一个池塘,如果有人能计算出池塘的准确面积.则池塘不计入土地价钱白白奉送.英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗
知识精讲
知识点一 用勾股定理在数轴上表示数
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都为1的直角三角形的斜边.长为 的线段能是直角边的长为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,直角边的长为正整数2, 3的直角三角形的斜边长为 .由此,可以依照如下方法在数轴上画出表示 的点.
如图,在数轴上找出表示3的点A, 则OA =3,过点A作直
线l 垂直于OA,在l上取点B,使AB = 2,以原点O为圆心,以
OB为半径作弧,弧与数轴的交点C即为表示 的点.
0
1
2
3
4
l
A
B
C
O
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边长为1和2,
∴斜边长为 ,即-1到A的距离是 ,
∴点A所表示的数为 .
注意:求点表示的数时注意画弧的起点不从原点起,则所表示的数不是斜边长.
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
归纳:
针对练习
1.如图,点C表示的数是( )
A.1 B. C.1.5 D.
D
2.如图,点A表示的实数是 ( )
D
3.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
A
知识点二 勾股定理在网格中的应用
例2 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).由勾股定理得
∴△ABC的周长为
归纳:勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
例3 如图,在2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,求AB边上的高.
解:如图,过点C作CD⊥AB于点D.
D
归纳:此类网格中求格点三角形的高的题,常用的方法是利用网格求面积,再用面积法求高.
针对练习
1.如图,在5×5的正方形网格中,每个小正方形的边长均为1,画出一个三角形的长分别为 .
A
B
C
解:如图所示.
2.如图,每个小正方形的边长均为1,则△ABC中,长为无理数的边有( )
A.0条
B.1条
C.2条
D.3条
C
知识点三 勾股定理在几何问题中的应用
例4 如图,在△ABC中,∠C=60°,AB=14,AC=10. 求BC的长.
解:如图,过点A作AD⊥BC于D.
∵∠ADC=90°,∠C=60°,
∴CD= ,AC=5.
在Rt△ACD中,AD
在Rt△ABD中,BD
∴BC=BD+CD=11+5=16.
例5 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,解得 x=3.
D
A
B
C
E
F
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线数或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
归纳:
针对练习
1.如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm
B.5 cm
C.6 cm
D.10 cm
B
2.如图,在等腰三角形ABC中,AB=AC,BC边上的高AD=6 cm,腰AB上的高CE=8 cm,则△ABC的周长等于________cm.
当堂检测
1.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
2.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
A.3
B.
C.5
D.
C
3.如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段________条.
8
4.如图,网格中的小正方形边长均为1,△ABC的三个顶点均在格点上,则AB边上的高为_______.
5.如图,等边三角形的边长是6.求:
(1)高AD的长;
(2)这个三角形的面积.
解:(1)由题意可知,在Rt△ADB中,
AB=6,BD= BC=3,∠ADB=90°.
由勾股定理,得AD=
(2)S△ABC= BC·AD= ×6×3
=
6.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿 AC折叠,点D落在点D′处,求重叠部分△AFC的面积.
解:易证△AFD′≌△CFB∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,
解得x=3.∴AF=AB-FB=8-3=5,
∴S△AFC= AF BC=10.
课堂小结
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
