1.5函数y=Asin(ωx+ψ)的图象课件
文档属性
| 名称 | 1.5函数y=Asin(ωx+ψ)的图象课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 480.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-18 00:00:00 | ||
图片预览





文档简介
课件33张PPT。高一数学组 函 数
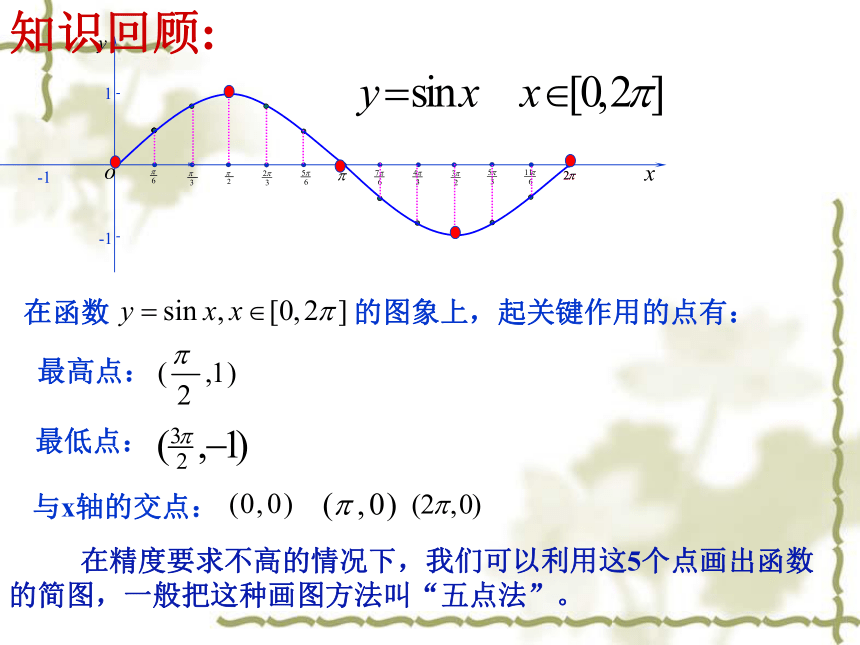
y=Asin(?x+?)的图象物理背景 在物理中,简谐振动中如单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y=Asin(ωx+φ) 的函数(其中A, ω, φ都是常数). 函数y=Asin(ωx+φ), (其中A>0, ω >0)表示一个振动量时, A就表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅; 往复一次所需的时间 ,称为这个振动的周期; 单位时间内往复振动的次数 ,称为振动的频率; 称为相位;x=0时的相位φ称为初相。在函数 的图象上,起关键作用的点有:最高点:最低点:与x轴的交点: 在精度要求不高的情况下,我们可以利用这5个点画出函数
的简图,一般把这种画图方法叫“五点法”。
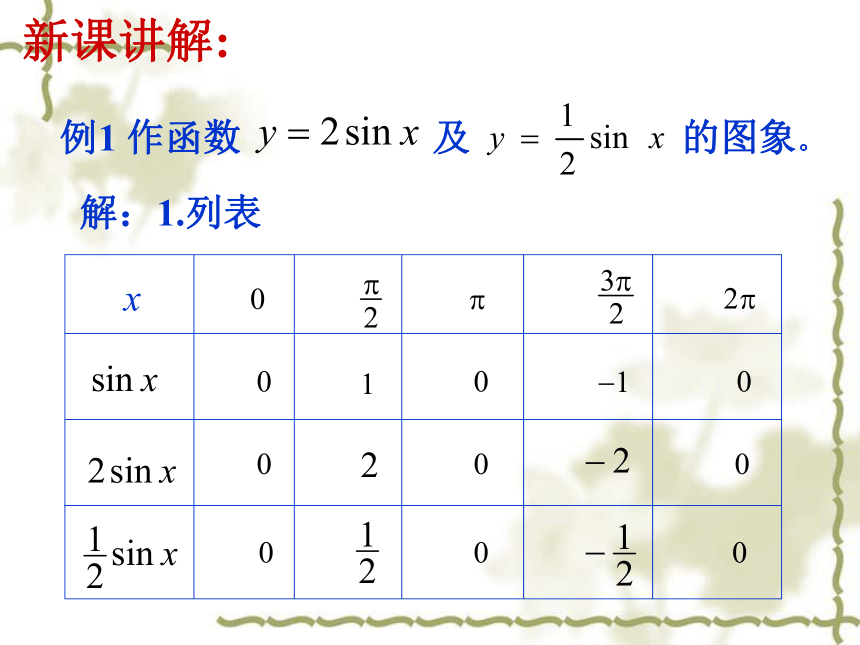
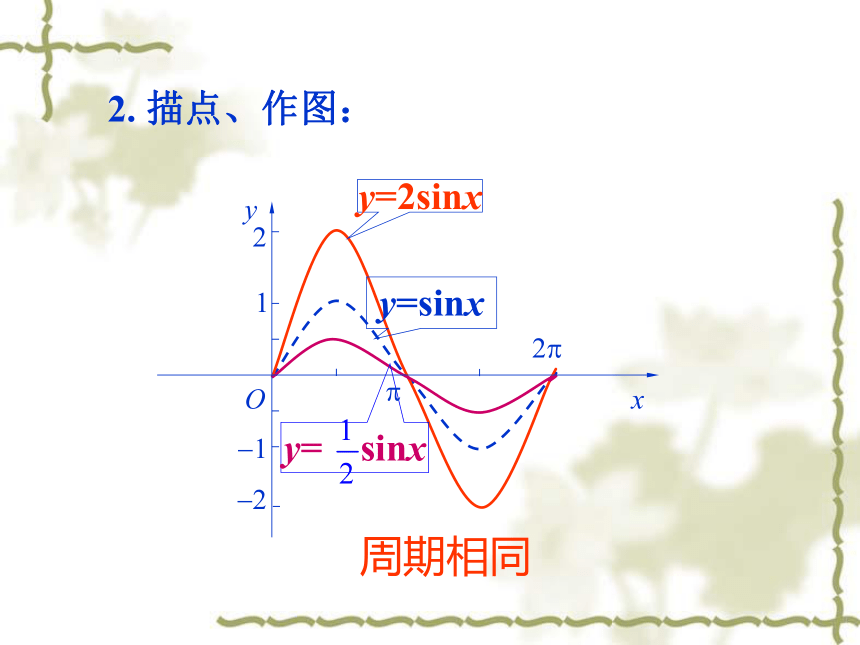
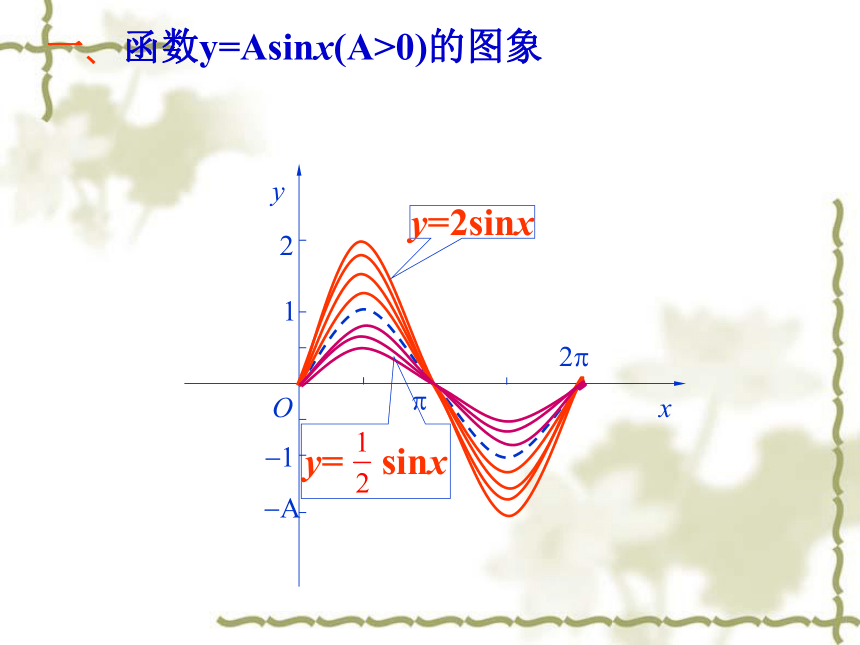
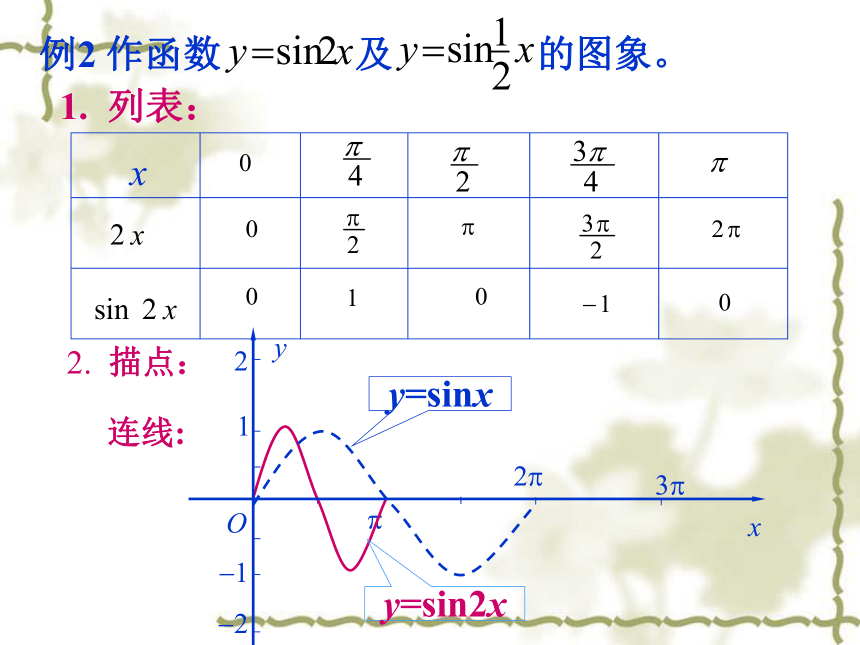
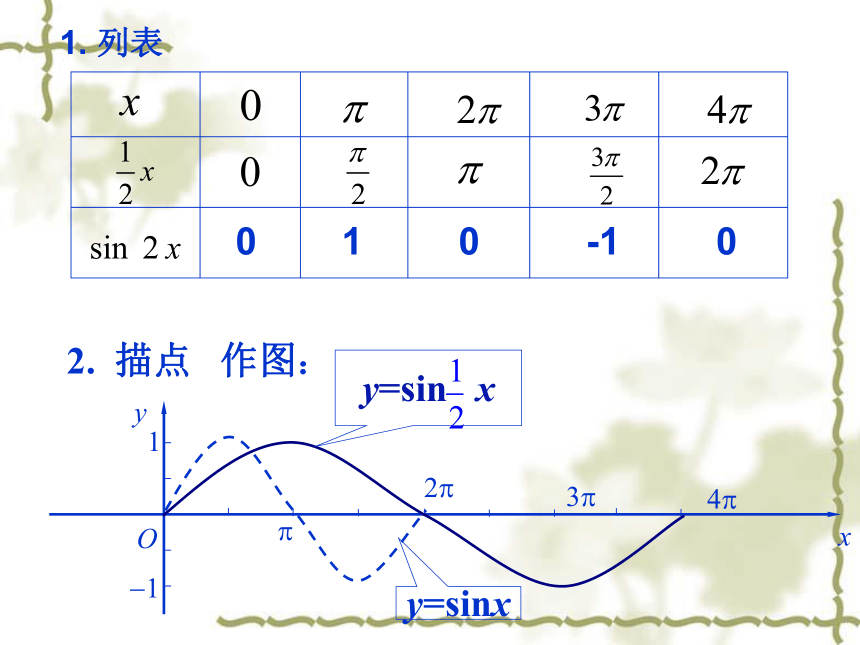
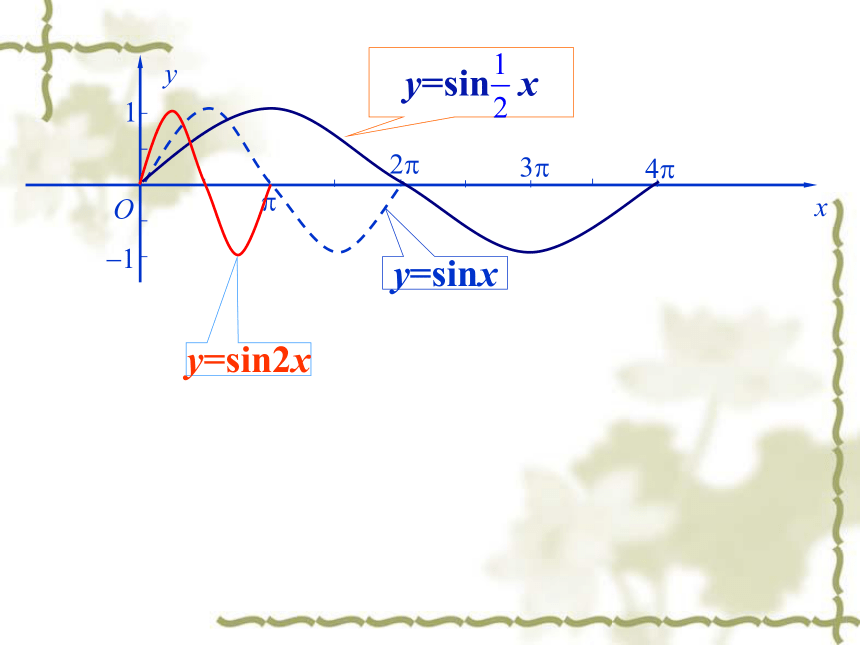
知识回顾:x例1 作函数 及 的图象。 解:1.列表新课讲解:y=2sinxy=sinxy= sinx2. 描点、作图:周期相同xyO?2?12?A?1y=2sinx一、函数y=Asinx(A>0)的图象y= sinx ? 函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0 y=sin 2x的图象可以看作是把 y=sinx的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变)。二、函数y=sin?x(?>0)的图象y=sin2xy=sinxy=sin x ?函数y=sin?x (? >0且?≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当00时)或向右(当φ<0时)平移|φ|个单位而得到的。结论三思考:函数y=f(x)与函数t=f(x+φ)的图像有何关系?例4 作函数 及 的图象。 作图y=sin2x四、函数y=sin(ωx+φ)与y=sinωx图象的关系例4 作函数 及 的图象。 x作图y=sin2x四、函数y=sin(ωx+φ)与y=sinωx图象的关系结论四?四、函数y=sinωx与 y=sin(ωx+φ)图象的关系 ?函数y=sin ( ?x + )(? >0且?≠1)的图象可以看作是把 y=sin ?x 的图象向左 (当 >0时)或向右(当 ﹤0时)平移 个单位而得到的。结论二思考:函数 与 的图像有何关系?提示:由于我们研究的函数仅限于? >0的情况,所以只需要判断 的正负即可判断平移方向思考:如果先伸缩变换再平移变换,只改变(2)(3)两步的顺序是否还能得到 ?向左或向右平移 个单位纵坐标不变,横坐标
变为原来的 倍纵坐标不变,横坐标
变为原来的 倍向左或向右平
移 个单位横坐标不变,纵坐标变为原来的A倍解:(画法一)
1、先把正弦曲线上所有的点向右平移 个单位长度,得
到 的图像。
2、把后者所有点的横坐标伸长为原来的3倍,纵坐标不
变,得到 的图像。
3、把所得的图像上所有点的纵坐标伸长为原来的 倍,
横坐标不变,而得到函数 的图像。解:(画法一)
1、先把后者所有点的横坐标伸长为原来的 倍,纵坐标不
变,得到 的图像。
2、再把正弦曲线上所有的点向右平移 个单位长度,得
到 的图像。
3、再把所得的图像上所有点的纵坐标伸长为原来的 倍,
横坐标不变,而得到函数 的图像。1-12-2xoy3-32?数学应用:例题 若函数 表示一个振动量:
⑴求这个振动的振幅、周期、初相;
⑵不用计算机和图形计算器,画出该函数的简图;
⑶根据函数的简图,写出函数的单调区间.解:设 ,则(2)描点(3)连线解:求单调增区间,可令求单调减区间,可令解得:解得:原函数的单调递增区间为:
单调递减区间为:课后作业:课本
P50 No.3、4;
P62 No.5(3)(4)7.
世上没有什么天才
天才是勤奋的结果
y=Asin(?x+?)的图象物理背景 在物理中,简谐振动中如单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y=Asin(ωx+φ) 的函数(其中A, ω, φ都是常数). 函数y=Asin(ωx+φ), (其中A>0, ω >0)表示一个振动量时, A就表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅; 往复一次所需的时间 ,称为这个振动的周期; 单位时间内往复振动的次数 ,称为振动的频率; 称为相位;x=0时的相位φ称为初相。在函数 的图象上,起关键作用的点有:最高点:最低点:与x轴的交点: 在精度要求不高的情况下,我们可以利用这5个点画出函数
的简图,一般把这种画图方法叫“五点法”。
知识回顾:x例1 作函数 及 的图象。 解:1.列表新课讲解:y=2sinxy=sinxy= sinx2. 描点、作图:周期相同xyO?2?12?A?1y=2sinx一、函数y=Asinx(A>0)的图象y= sinx ? 函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0
变为原来的 倍纵坐标不变,横坐标
变为原来的 倍向左或向右平
移 个单位横坐标不变,纵坐标变为原来的A倍解:(画法一)
1、先把正弦曲线上所有的点向右平移 个单位长度,得
到 的图像。
2、把后者所有点的横坐标伸长为原来的3倍,纵坐标不
变,得到 的图像。
3、把所得的图像上所有点的纵坐标伸长为原来的 倍,
横坐标不变,而得到函数 的图像。解:(画法一)
1、先把后者所有点的横坐标伸长为原来的 倍,纵坐标不
变,得到 的图像。
2、再把正弦曲线上所有的点向右平移 个单位长度,得
到 的图像。
3、再把所得的图像上所有点的纵坐标伸长为原来的 倍,
横坐标不变,而得到函数 的图像。1-12-2xoy3-32?数学应用:例题 若函数 表示一个振动量:
⑴求这个振动的振幅、周期、初相;
⑵不用计算机和图形计算器,画出该函数的简图;
⑶根据函数的简图,写出函数的单调区间.解:设 ,则(2)描点(3)连线解:求单调增区间,可令求单调减区间,可令解得:解得:原函数的单调递增区间为:
单调递减区间为:课后作业:课本
P50 No.3、4;
P62 No.5(3)(4)7.
世上没有什么天才
天才是勤奋的结果
