华师大版数学八年级上册13.3.2等腰三角形的判定 课件(共20张PPT)
文档属性
| 名称 | 华师大版数学八年级上册13.3.2等腰三角形的判定 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 14:12:54 | ||
图片预览






文档简介
(共20张PPT)
..\get (5).jpg
等腰三角形的判定
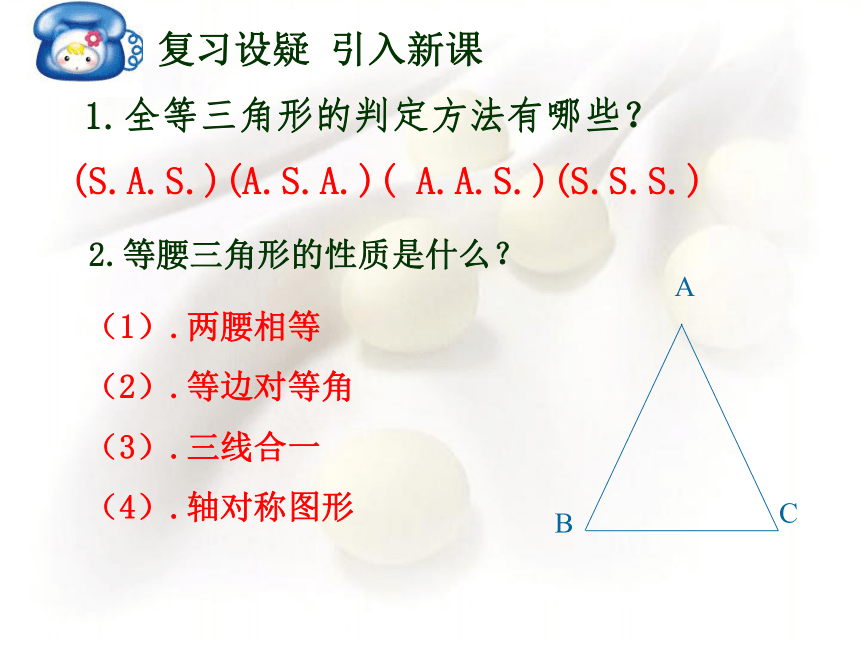
复习设疑 引入新课
1.全等三角形的判定方法有哪些?
2.等腰三角形的性质是什么?
(1).两腰相等
(2).等边对等角
(3).三线合一
(4).轴对称图形
A
B
C
(S.A.S.)(A.S.A.)( A.A.S.)(S.S.S.)
如果一个三角形有两条边相等,那么这两条边所对的角也相等.
3.将命题“等边对等角”写成“如果…那么…”的形式.
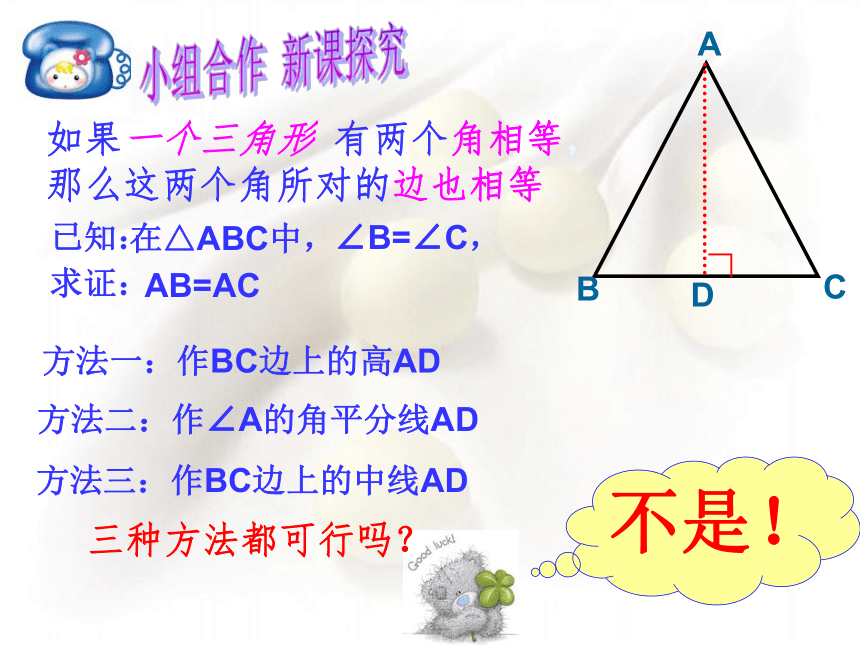
把这个命题de反过来:在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
已知:
A
B
C
D
方法一:作BC边上的高AD
方法二:作∠A的角平分线AD
方法三:作BC边上的中线AD
在△ABC中,
∠B=∠C,
求证:
AB=AC
∟
不是!
如果一个三角形 有两个角相等,那么这两个角所对的边也相等.
三种方法都可行吗?
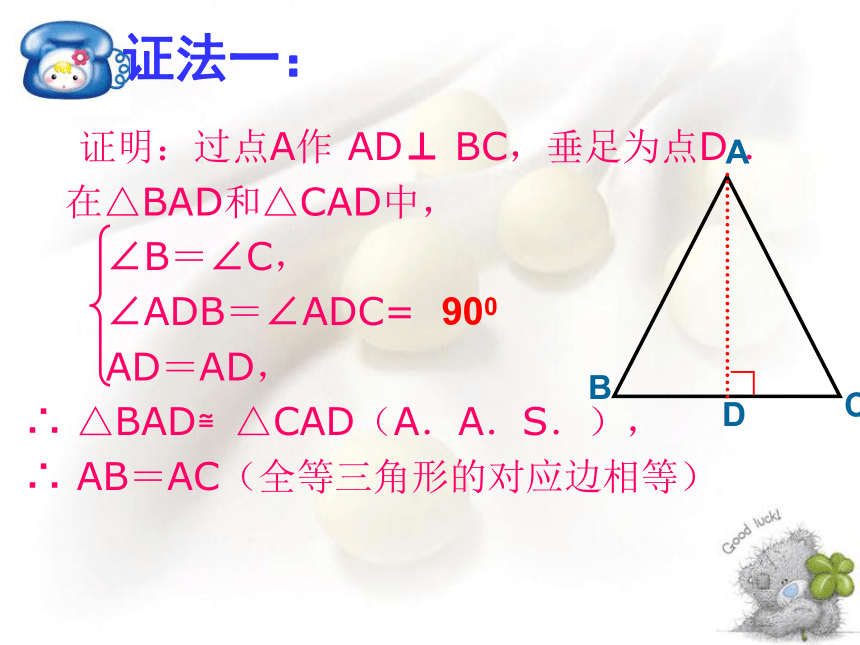
证明:过点A作 AD⊥ BC,垂足为点D .
在△BAD和△CAD中,
∠B=∠C,
∠ADB=∠ADC=
AD=AD,
∴ △BAD≌△CAD(A.A.S.),
∴ AB=AC(全等三角形的对应边相等)
900
A
B
C
∟
D
证法一:
证明:过点A作∠BAC的平分线AD.
在△BAD和△CAD中,
∠B=∠C,
∠1=∠2,
AD=AD,
∴ △BAD≌△CAD(A.A.S.),
∴ AB=AC(全等三角形的对应边相等)
证法二:
归纳:如果一个三角形有两个角相等,那么这两个角所对的边也相等。(简写成“等角对等边”)
例1.如图,在△ABC中,已知∠A=40°,∠B=70°。
求证:AB=AC
证明:∵∠A+∠B+∠C=180°(三角 形内角和180°)∠A=40° ∠B=70°(已知)
∴∠C=180°-∠A-∠B(等式的性质)
=180°-40°-70°=70°
∴∠B=∠C(等量代换)
∴AB=AC(等角对等边)
A
B
C
40°
70°
例2:如图:AB∥CD,∠1=∠2
求证:AB=AC
证明:∵ AB∥CD (已知)
∴∠B=∠2(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠B=∠1(等量代换)
∴AB=AC(等角对等边)
1
2
A
B
C
D
1.三个角都相等三角形是等边三角形。
2.有一个角等于60°的等腰三角形是等边三角形。
利用“等角对等边”证明请同学们试一试
基本应用
证明:在△ ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
A
B
C
已知:在△ ABC中∠A=∠B=∠C
求证:AB=BC=CA
例2、如图,把一张长方形的纸沿对角线折叠,重合的部分是一个等腰三角形吗?为什么?
A
B
C
G
D
E
1
2
3
解:重合部分是等腰三角形。
理由:由ABDC是长方形知
AC∥BD
∴∠ 3= ∠ 2
由沿对角线折叠可知
∠ 1 = ∠ 2
∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)
知识迁移:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.
(1)请问图中有多少个等腰三角形 说明理由.
(2)线段EF和线段EB,FC之间有什么关系
AB=AC
AB≠AC
B
0
C
A
E
F
过点O作直线EF//BC交AB于E,交AC于F.
通过本节课的学习你有什么收获?和大家交流一下。
.
课堂小结:
1、等腰三角形的判定定理是什么?
2、等腰三角形的判定方法有下列几种:
①定义 ②判定定理
3、等腰三角形的判定定理与性质定理
的区别是:条件和结论刚好相反。
4、运用等腰三角形的判定定理时,
应注意在同一个三角形中
性质是:等边 等角
判定是:等角 等边
寄语
择善人而交,择善书 而读,择善言而听,择善行而从。
..\get (5).jpg
等腰三角形的判定
复习设疑 引入新课
1.全等三角形的判定方法有哪些?
2.等腰三角形的性质是什么?
(1).两腰相等
(2).等边对等角
(3).三线合一
(4).轴对称图形
A
B
C
(S.A.S.)(A.S.A.)( A.A.S.)(S.S.S.)
如果一个三角形有两条边相等,那么这两条边所对的角也相等.
3.将命题“等边对等角”写成“如果…那么…”的形式.
把这个命题de反过来:在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
已知:
A
B
C
D
方法一:作BC边上的高AD
方法二:作∠A的角平分线AD
方法三:作BC边上的中线AD
在△ABC中,
∠B=∠C,
求证:
AB=AC
∟
不是!
如果一个三角形 有两个角相等,那么这两个角所对的边也相等.
三种方法都可行吗?
证明:过点A作 AD⊥ BC,垂足为点D .
在△BAD和△CAD中,
∠B=∠C,
∠ADB=∠ADC=
AD=AD,
∴ △BAD≌△CAD(A.A.S.),
∴ AB=AC(全等三角形的对应边相等)
900
A
B
C
∟
D
证法一:
证明:过点A作∠BAC的平分线AD.
在△BAD和△CAD中,
∠B=∠C,
∠1=∠2,
AD=AD,
∴ △BAD≌△CAD(A.A.S.),
∴ AB=AC(全等三角形的对应边相等)
证法二:
归纳:如果一个三角形有两个角相等,那么这两个角所对的边也相等。(简写成“等角对等边”)
例1.如图,在△ABC中,已知∠A=40°,∠B=70°。
求证:AB=AC
证明:∵∠A+∠B+∠C=180°(三角 形内角和180°)∠A=40° ∠B=70°(已知)
∴∠C=180°-∠A-∠B(等式的性质)
=180°-40°-70°=70°
∴∠B=∠C(等量代换)
∴AB=AC(等角对等边)
A
B
C
40°
70°
例2:如图:AB∥CD,∠1=∠2
求证:AB=AC
证明:∵ AB∥CD (已知)
∴∠B=∠2(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠B=∠1(等量代换)
∴AB=AC(等角对等边)
1
2
A
B
C
D
1.三个角都相等三角形是等边三角形。
2.有一个角等于60°的等腰三角形是等边三角形。
利用“等角对等边”证明请同学们试一试
基本应用
证明:在△ ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
A
B
C
已知:在△ ABC中∠A=∠B=∠C
求证:AB=BC=CA
例2、如图,把一张长方形的纸沿对角线折叠,重合的部分是一个等腰三角形吗?为什么?
A
B
C
G
D
E
1
2
3
解:重合部分是等腰三角形。
理由:由ABDC是长方形知
AC∥BD
∴∠ 3= ∠ 2
由沿对角线折叠可知
∠ 1 = ∠ 2
∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)
知识迁移:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.
(1)请问图中有多少个等腰三角形 说明理由.
(2)线段EF和线段EB,FC之间有什么关系
AB=AC
AB≠AC
B
0
C
A
E
F
过点O作直线EF//BC交AB于E,交AC于F.
通过本节课的学习你有什么收获?和大家交流一下。
.
课堂小结:
1、等腰三角形的判定定理是什么?
2、等腰三角形的判定方法有下列几种:
①定义 ②判定定理
3、等腰三角形的判定定理与性质定理
的区别是:条件和结论刚好相反。
4、运用等腰三角形的判定定理时,
应注意在同一个三角形中
性质是:等边 等角
判定是:等角 等边
寄语
择善人而交,择善书 而读,择善言而听,择善行而从。
