华师大版八年级上册14.1.1直角三角形三边的关系 课件(共18张PPT)
文档属性
| 名称 | 华师大版八年级上册14.1.1直角三角形三边的关系 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-05 12:26:11 | ||
图片预览



文档简介
(共18张PPT)
2002年在北京召开的国际数学家大会(ICM2002)。在那个大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明一个伟大数学定理—勾股定理的弦图.该图隐含着直角三角形三边之间的一种奇妙关系
14.1勾股定理
a
b
c
1.直角三角形三边的关系
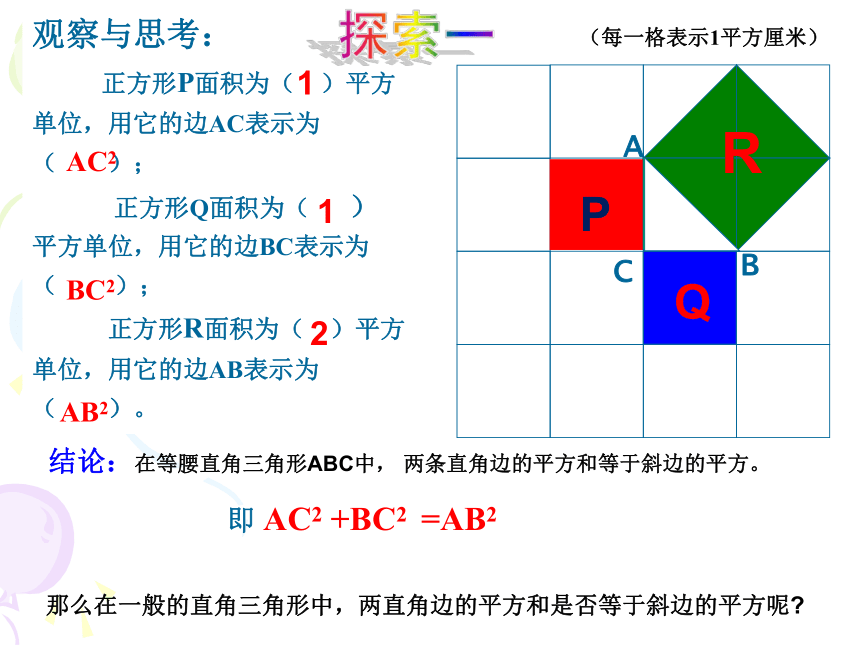
观察与思考:
正方形P面积为( )平方单位,用它的边AC表示为( );
正方形Q面积为( )
平方单位,用它的边BC表示为( );
正方形R面积为( )平方单位,用它的边AB表示为( )。
结论:在等腰直角三角形ABC中, 两条直角边的平方和等于斜边的平方。
即 AC2 +BC2 =AB2
A
B
C
(每一格表示1平方厘米)
那么在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢
1
AC2
1
BC2
2
AB2
P
Q
R
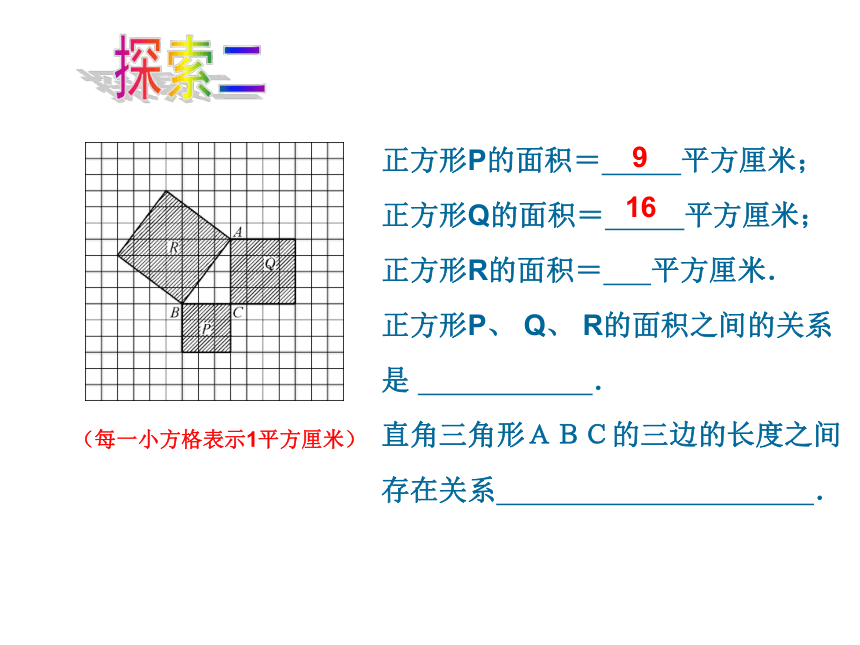
正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
直角三角形ABC的三边的长度之间存在关系 .
(每一小方格表示1平方厘米)
9
16
Q
R
P
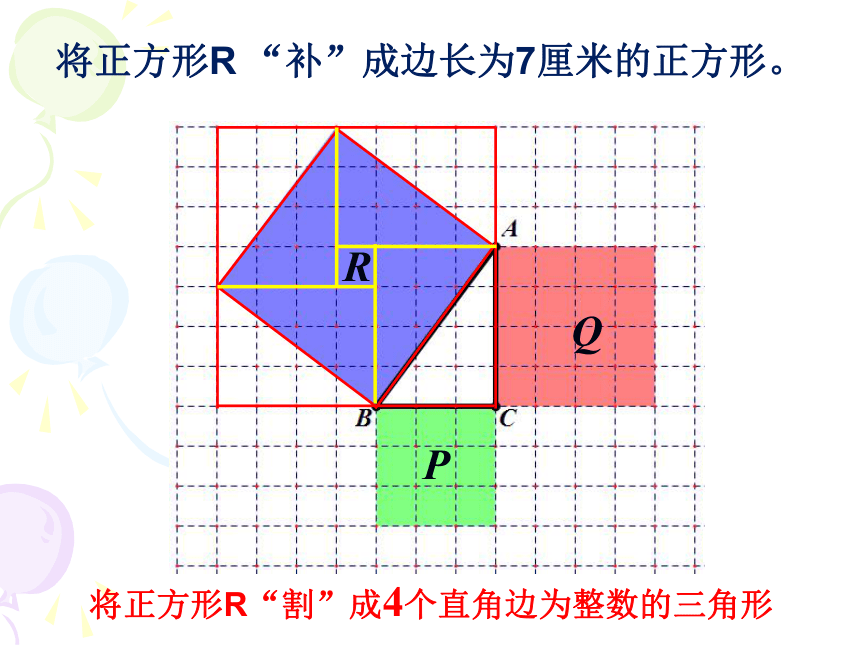
将正方形R“割”成4个直角边为整数的三角形
将正方形R “补”成边长为7厘米的正方形。
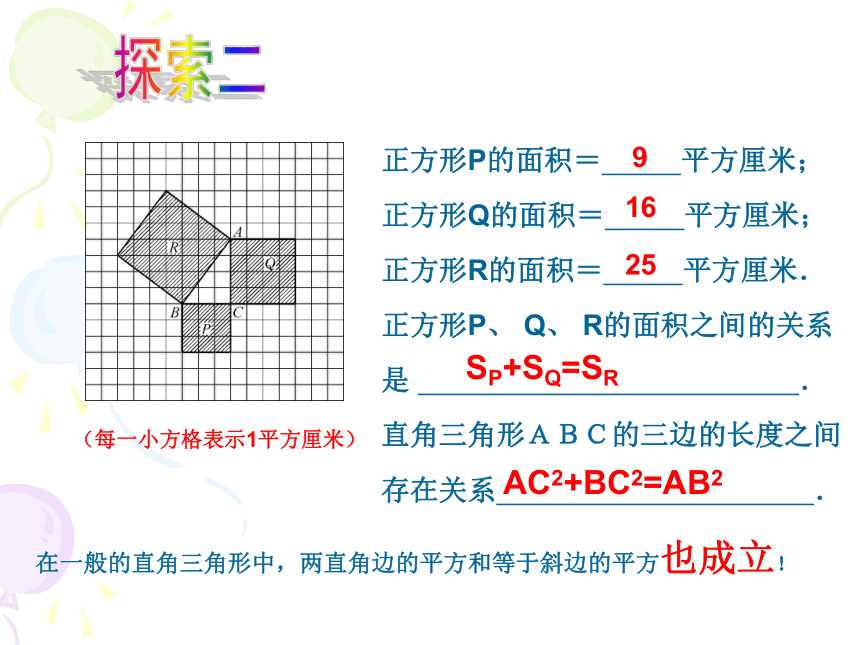
正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
直角三角形ABC的三边的长度之间存在关系 .
(每一小方格表示1平方厘米)
9
16
25
SP+SQ=SR
AC2+BC2=AB2
在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立!
在练习本上,用三角尺画出两条直角边分别为5cm、 12cm的直角三角形,然后用刻度尺量出斜边的长,并验证关系“两直角边的平方和等于斜边的平方”对这个直角三角形是否成立.
5
12
13
52+122=
169
132=169
成立
对于任意的直角三角形,如果它的两条直角边分别为a、 b,斜边为c,那么一定有a2+b2=c2。
勾股定理:
a
b
c
直角三角形两直角边的平方和等于斜边的平方
数学语言描述:
如图,在Rt△ABC中,若a、b为直角边,c为斜边,则有a2+b2=c2
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 它标志着中国古代的数学成就。
弦
股
勾
图1-1
a
b
c
如图,弦图是由4个全等的直角三角形与小正方形组成的大正方形,你能借助这个图形来证明勾股定理吗?
思考
除此之外还有没有别的拼图方法来证明呢?
大正方形的面积等于c2,同时它的面积又等于四个全等的直角三角形的面积之和,于是有 +(b-a)2=c2化简即得a2+ b2=c2
如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
b
a
b
a
b
a
b
a
c
c
c
c
在Rt△ABC中,已知∠B=90°,AB=6,BC=8.求AC的长.
例题
应用勾股定理,由直角三角形任意两边的长度,可以求出第三边的长度,关键是明确各边角关系,灵活运用公式及其变式。
1. 如图,在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c
已知: b=8, c=10 , 求a
已知: a=7, c=25, 求b
A
b
解:由勾股定理得:
(2)
(3)
(1)
小试牛刀
2、若一个直角三角形的三边长分别为3,4, 求第三边 的长度
小试牛刀
(1)如图
4
3
4
3
(2)如图
解:由勾股定理得:
∴
∴
或
解:由勾股定理得:
∴
学习小结
请你谈一谈你这节课的收获与感悟.
(2) 运用“勾股定理”时应注意什么问题?
(1)这节课你学到了什么知识?
①勾股定理:直角三角形两直角边的平方和等于斜边的平方
②在直角三角形中,已知任意两边,可以用勾股定理求第三边。
小结
①要利用图形找到未知边所在的直角三角形;
②看清未知边是所在直角三角形的哪一边;
③勾股定理要用对。
再见
2002年在北京召开的国际数学家大会(ICM2002)。在那个大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明一个伟大数学定理—勾股定理的弦图.该图隐含着直角三角形三边之间的一种奇妙关系
14.1勾股定理
a
b
c
1.直角三角形三边的关系
观察与思考:
正方形P面积为( )平方单位,用它的边AC表示为( );
正方形Q面积为( )
平方单位,用它的边BC表示为( );
正方形R面积为( )平方单位,用它的边AB表示为( )。
结论:在等腰直角三角形ABC中, 两条直角边的平方和等于斜边的平方。
即 AC2 +BC2 =AB2
A
B
C
(每一格表示1平方厘米)
那么在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢
1
AC2
1
BC2
2
AB2
P
Q
R
正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
直角三角形ABC的三边的长度之间存在关系 .
(每一小方格表示1平方厘米)
9
16
Q
R
P
将正方形R“割”成4个直角边为整数的三角形
将正方形R “补”成边长为7厘米的正方形。
正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
直角三角形ABC的三边的长度之间存在关系 .
(每一小方格表示1平方厘米)
9
16
25
SP+SQ=SR
AC2+BC2=AB2
在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立!
在练习本上,用三角尺画出两条直角边分别为5cm、 12cm的直角三角形,然后用刻度尺量出斜边的长,并验证关系“两直角边的平方和等于斜边的平方”对这个直角三角形是否成立.
5
12
13
52+122=
169
132=169
成立
对于任意的直角三角形,如果它的两条直角边分别为a、 b,斜边为c,那么一定有a2+b2=c2。
勾股定理:
a
b
c
直角三角形两直角边的平方和等于斜边的平方
数学语言描述:
如图,在Rt△ABC中,若a、b为直角边,c为斜边,则有a2+b2=c2
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 它标志着中国古代的数学成就。
弦
股
勾
图1-1
a
b
c
如图,弦图是由4个全等的直角三角形与小正方形组成的大正方形,你能借助这个图形来证明勾股定理吗?
思考
除此之外还有没有别的拼图方法来证明呢?
大正方形的面积等于c2,同时它的面积又等于四个全等的直角三角形的面积之和,于是有 +(b-a)2=c2化简即得a2+ b2=c2
如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
b
a
b
a
b
a
b
a
c
c
c
c
在Rt△ABC中,已知∠B=90°,AB=6,BC=8.求AC的长.
例题
应用勾股定理,由直角三角形任意两边的长度,可以求出第三边的长度,关键是明确各边角关系,灵活运用公式及其变式。
1. 如图,在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c
已知: b=8, c=10 , 求a
已知: a=7, c=25, 求b
A
b
解:由勾股定理得:
(2)
(3)
(1)
小试牛刀
2、若一个直角三角形的三边长分别为3,4, 求第三边 的长度
小试牛刀
(1)如图
4
3
4
3
(2)如图
解:由勾股定理得:
∴
∴
或
解:由勾股定理得:
∴
学习小结
请你谈一谈你这节课的收获与感悟.
(2) 运用“勾股定理”时应注意什么问题?
(1)这节课你学到了什么知识?
①勾股定理:直角三角形两直角边的平方和等于斜边的平方
②在直角三角形中,已知任意两边,可以用勾股定理求第三边。
小结
①要利用图形找到未知边所在的直角三角形;
②看清未知边是所在直角三角形的哪一边;
③勾股定理要用对。
再见
