幂函数、一次函数、二次函数[上学期]
图片预览



文档简介
课件19张PPT。2.9 幂函数、一次函数、二次函数一、幂函数<->幂函数定义
形如y=xa(a∈R)的函数。其中a为常数。<二>幂函数的性质
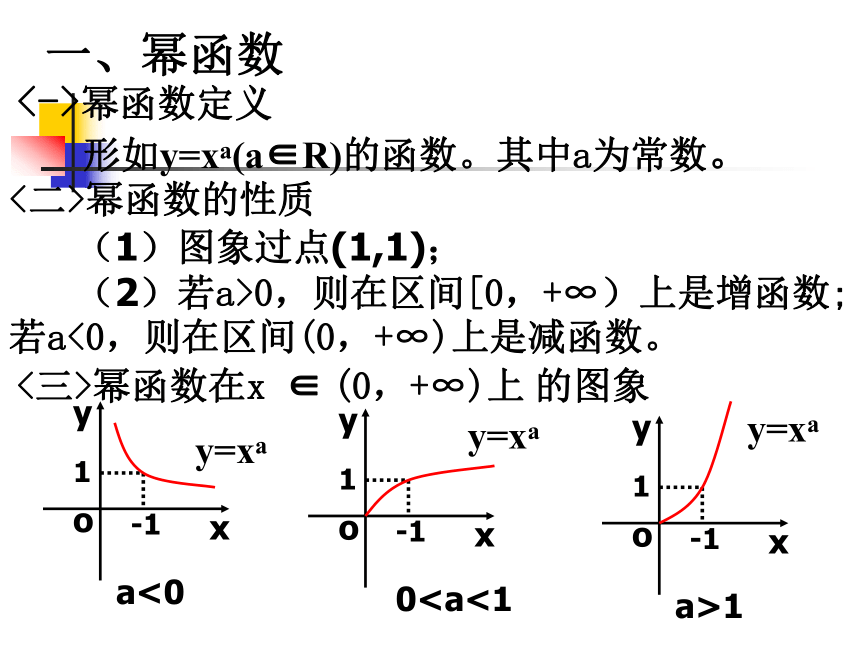
(1)图象过点(1,1);
(2)若a>0,则在区间[0,+∞)上是增函数;
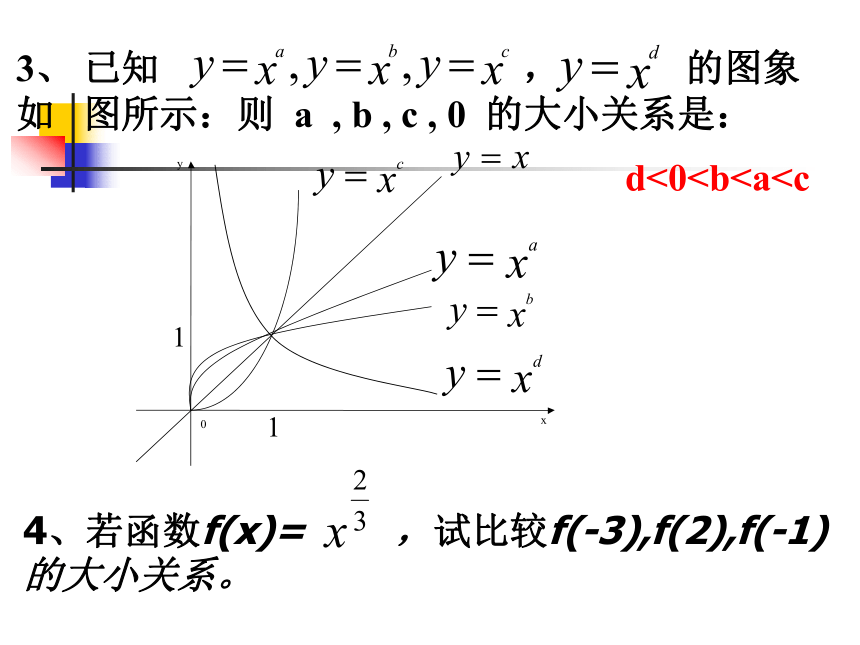
若a<0,则在区间(0,+∞)上是减函数。<三>幂函数在x ∈ (0,+∞)上 的图象<四>基础知识点击2、(1)若幂函数f(x)= 是偶函数,且在x∈(0,+∞)上是减函数,f(x)= . (2)若幂函数 的图象 过原点,则m= .3、 已知 , 的图象如 图所示:则 a , b , c , 0 的大小关系是: d<0的大小关系。二、一次函数<一>定义
形如y=kx+b(k≠0)的函数。<二>基础知识点击 直线ax+by+c=0(ab>0,ac<0)一定不
过哪个象限?三、二次函数<一>二次函数的图象应用1、二次函数f(x)=ax2+bx+c(a≠0)
的图象如右图试确定下列各式的
正负:a ;b ;c ;a-b+c ;
b2-4ac ;a+b+c ;2、下列图中 与
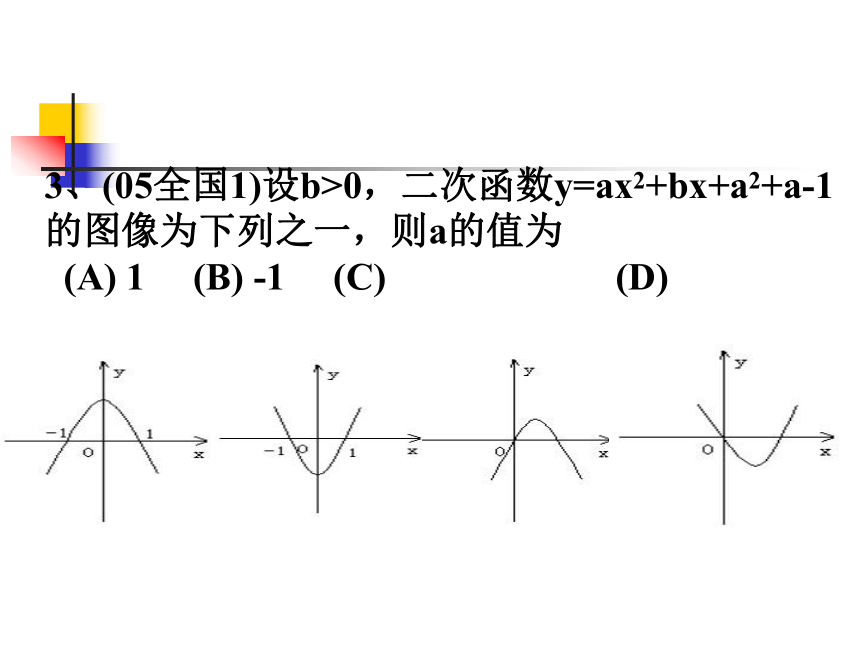
的图像只可能是 3、(05全国1)设b>0,二次函数y=ax2+bx+a2+a-1
的图像为下列之一,则a的值为
(A) 1 (B) -1 (C) (D)
<二>二次函数性质的应用1.二次函数f(x)满足f(3+x)=f(3-x)且f(x)=0有两
个实根x1,x2,则x1+x2等于_________.2.函数f(x)=2x2-mx+3,当x∈(-∞,-1]时是减函
数,当x∈(-1,+∞)时是增函数,则f(2)= _______.
4、函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函
数,则f(1)的取值范围是 .3、已知函数 f(x)=ax2+4x+c,且f(-1)=0,f(3)=0,
则函数f(x)在区间[-2,2]上的增区间为 。<三>二次函数解析式求法1、已知二次函数y=f(x)满足f(x-1)=f(-x-1),
且f(x)的最大值是8,f(-2)=7,求f(x)。2、已知二次函数f(x)满足f(1)=f(3)=0,且f(x)
的图象过点(4,-3),求f(x)。[解题回顾]二次函数的解析表达式有
①一般式 f(x)=ax2+bx+c(a≠0);
②顶点式 f(x)=a(x-k)2+m(a≠0);
③零点式 f(x)=a(x-x1)(x-x2)(a≠0) 1、函数f(x)=2x2-6x+1的最大值 ,
最小值是 ;f(x)在区间[-1,1]上
的最小值是_____,最大值是____.<四>二次函数最值求法[解题回顾](1).二次函数f(x)=ax2+bx+c(a≠0),若a>0 (或a<0),
则当x= 时, (或fmax(x)= )
(2).二次函数f(x)=ax2+bx+c(a≠0)在区间[p,q]上的最值问题.
一般情况下,需要分:
<p,p≤ ≤q和 >q三种情况讨论解决. 2、函数=-x2+2ax+1-a在区间[0,1]上的最
大值为2,求实数a的值.【解题回顾】(1)含有参数的二次函数的最值问题,因其顶点相对于定义域区间的位置不同,其最值状况也不同.所以要根据二者的相关位置进行分类讨论
(2)本题是“定”二次函数,“动”区间,依照此法也可以讨论“动”二次函数,“定”区间的二次函数问题 3.函数f(x)=x2-4x-4在闭区间[t,t+1](t∈R)上的最小值记为g(t).
(1)试写出g(t)的函数表达式;
(2)作g(t)的图象并写出g(t)的最小值<五>一元二次方程根的分布 一般地对于含有字母的一元二次方程ax2+bx+c=0的实数根的分布问题,有如下结论:令f(x)=ax2+bx+c(不妨设a>0) 二次方程f(x)=ax2+bx+c=0的区间根问题.一般情况下,需要从三个方面考虑:
①判别式; ②区间端点函数值的正负;
③对称轴 x= 与区间端点的关系①若两根都小于实数α,则有②若两根都大于实数α,则有 ③若两根在区间(α,β)内,则有 ④若一根小于α,另一根小于β,则有 ⑤若两根中只有一根在区间(α,β)内,则有 1、若方程7x2-(k+13)x+k2-k-2=0的
两根分别在(0,1)和(1,2)内,求k的取值范围.2、已知A={x|x2+(p+2)x+1=0,x∈R},
且A∩R+=φ,则实数p的范围是_________.3.已知函数f(x)=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,求实数m的取值范围 【解题回顾】①在本题解题过程中,容易将f(x)=mx2+(m-3)x+1看成是二次函数,从而忽视对m=0的讨论
②实系数方程ax2+bx+c=0(a≠0)的两实根异号的充要条件
为 ;有两正实根的充要条件是 ;有两负实
根的充要条件是(05全国卷Ⅰ)已知二次函数f(x)的二次项
系数为a,且不等式f(x)>-2x的解集为(1,3)。
(Ⅰ)若方程f(x)+6a=0有两个相等的根,求
的解析式;
(Ⅱ)若f(x)的最大值为正数,求a的取值范围。误解分析2.二次函数、一元二次不等式和一元二次方程是一个有机的整体,要深刻理解它们之间的关系,运用函数方程的思想方法将它们进行相互转化,才是准确迅速答题的关键.1.在讨论方程根的分布情况时,要写出它的充要条件,注意观察方程对应的函数图象是避免将充要条件写成必要条件的有效办法.
形如y=xa(a∈R)的函数。其中a为常数。<二>幂函数的性质
(1)图象过点(1,1);
(2)若a>0,则在区间[0,+∞)上是增函数;
若a<0,则在区间(0,+∞)上是减函数。<三>幂函数在x ∈ (0,+∞)上 的图象<四>基础知识点击2、(1)若幂函数f(x)= 是偶函数,且在x∈(0,+∞)上是减函数,f(x)= . (2)若幂函数 的图象 过原点,则m= .3、 已知 , 的图象如 图所示:则 a , b , c , 0 的大小关系是: d<0
形如y=kx+b(k≠0)的函数。<二>基础知识点击 直线ax+by+c=0(ab>0,ac<0)一定不
过哪个象限?三、二次函数<一>二次函数的图象应用1、二次函数f(x)=ax2+bx+c(a≠0)
的图象如右图试确定下列各式的
正负:a ;b ;c ;a-b+c ;
b2-4ac ;a+b+c ;2、下列图中 与
的图像只可能是 3、(05全国1)设b>0,二次函数y=ax2+bx+a2+a-1
的图像为下列之一,则a的值为
(A) 1 (B) -1 (C) (D)
<二>二次函数性质的应用1.二次函数f(x)满足f(3+x)=f(3-x)且f(x)=0有两
个实根x1,x2,则x1+x2等于_________.2.函数f(x)=2x2-mx+3,当x∈(-∞,-1]时是减函
数,当x∈(-1,+∞)时是增函数,则f(2)= _______.
4、函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函
数,则f(1)的取值范围是 .3、已知函数 f(x)=ax2+4x+c,且f(-1)=0,f(3)=0,
则函数f(x)在区间[-2,2]上的增区间为 。<三>二次函数解析式求法1、已知二次函数y=f(x)满足f(x-1)=f(-x-1),
且f(x)的最大值是8,f(-2)=7,求f(x)。2、已知二次函数f(x)满足f(1)=f(3)=0,且f(x)
的图象过点(4,-3),求f(x)。[解题回顾]二次函数的解析表达式有
①一般式 f(x)=ax2+bx+c(a≠0);
②顶点式 f(x)=a(x-k)2+m(a≠0);
③零点式 f(x)=a(x-x1)(x-x2)(a≠0) 1、函数f(x)=2x2-6x+1的最大值 ,
最小值是 ;f(x)在区间[-1,1]上
的最小值是_____,最大值是____.<四>二次函数最值求法[解题回顾](1).二次函数f(x)=ax2+bx+c(a≠0),若a>0 (或a<0),
则当x= 时, (或fmax(x)= )
(2).二次函数f(x)=ax2+bx+c(a≠0)在区间[p,q]上的最值问题.
一般情况下,需要分:
<p,p≤ ≤q和 >q三种情况讨论解决. 2、函数=-x2+2ax+1-a在区间[0,1]上的最
大值为2,求实数a的值.【解题回顾】(1)含有参数的二次函数的最值问题,因其顶点相对于定义域区间的位置不同,其最值状况也不同.所以要根据二者的相关位置进行分类讨论
(2)本题是“定”二次函数,“动”区间,依照此法也可以讨论“动”二次函数,“定”区间的二次函数问题 3.函数f(x)=x2-4x-4在闭区间[t,t+1](t∈R)上的最小值记为g(t).
(1)试写出g(t)的函数表达式;
(2)作g(t)的图象并写出g(t)的最小值<五>一元二次方程根的分布 一般地对于含有字母的一元二次方程ax2+bx+c=0的实数根的分布问题,有如下结论:令f(x)=ax2+bx+c(不妨设a>0) 二次方程f(x)=ax2+bx+c=0的区间根问题.一般情况下,需要从三个方面考虑:
①判别式; ②区间端点函数值的正负;
③对称轴 x= 与区间端点的关系①若两根都小于实数α,则有②若两根都大于实数α,则有 ③若两根在区间(α,β)内,则有 ④若一根小于α,另一根小于β,则有 ⑤若两根中只有一根在区间(α,β)内,则有 1、若方程7x2-(k+13)x+k2-k-2=0的
两根分别在(0,1)和(1,2)内,求k的取值范围.2、已知A={x|x2+(p+2)x+1=0,x∈R},
且A∩R+=φ,则实数p的范围是_________.3.已知函数f(x)=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,求实数m的取值范围 【解题回顾】①在本题解题过程中,容易将f(x)=mx2+(m-3)x+1看成是二次函数,从而忽视对m=0的讨论
②实系数方程ax2+bx+c=0(a≠0)的两实根异号的充要条件
为 ;有两正实根的充要条件是 ;有两负实
根的充要条件是(05全国卷Ⅰ)已知二次函数f(x)的二次项
系数为a,且不等式f(x)>-2x的解集为(1,3)。
(Ⅰ)若方程f(x)+6a=0有两个相等的根,求
的解析式;
(Ⅱ)若f(x)的最大值为正数,求a的取值范围。误解分析2.二次函数、一元二次不等式和一元二次方程是一个有机的整体,要深刻理解它们之间的关系,运用函数方程的思想方法将它们进行相互转化,才是准确迅速答题的关键.1.在讨论方程根的分布情况时,要写出它的充要条件,注意观察方程对应的函数图象是避免将充要条件写成必要条件的有效办法.
