函数的表示方法[上学期]

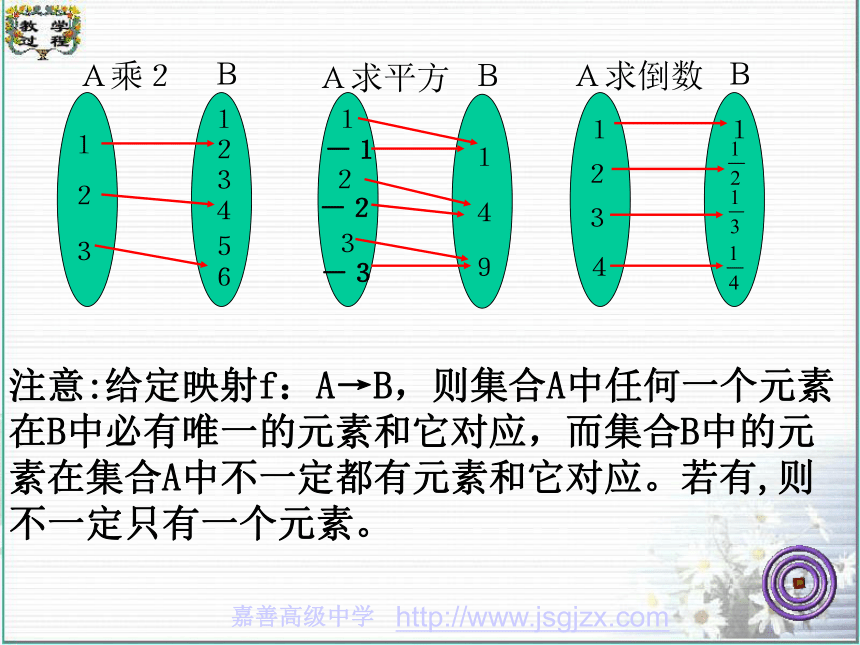
课件10张PPT。注意:给定映射f：A→B，则集合A中任何一个元素在B中必有唯一的元素和它对应，而集合B中的元素在集合A中不一定都有元素和它对应。若有,则不一定只有一个元素。判断下列对应是否是映射？为什么？1、设A={1，2，3，4}，B={3，4，5，6，7，8，9}，对应关系f：“乘2加1”，f：A→B2、设A=N+，B={0，1}，对应关系f：“除以2得的余数”，f：A→B
3、设A={x|x是三角形}，B={y|y>0},对应关系f：“计算面积”，f：A→B
4、设A=R，B={直线上的点}，对应关系f：“A中的数与B中的点对应”，f：A→B
5、设A={P|P是直角坐标系中的点}，B={（x，y）|x∈R，y∈R}，对应关系f：“按照建立直角坐标系的方法，使A中的点P与B中的有序实数对（x，y）对应”，f：A→B
思考1、给定两个集合A、B和由A的B的对应关系f，如何判断这个对应是否是映射？结论：若对于集合A中的任何一个元素，在集合B中都有唯一的元素和它对应，那么这个对应就是映射，否则就不是映射。思考2：什么样的对应是映射？（一对一，多对一）求函数的解析式求函数解析式的常用方法有:1、代入法：例1:已知f(x)=x2-1,求f(x+x2)变式:已知 求2、代定系数法：已知f（x）的函数类型，要求f（x）的解析式时，可根据类型设其解析式，从而确定其系数。例题2:已知f(x)是一次函数,且f[f(x)]=x+6,求f(x)例题3:f(x)是二次函数,且f(0)=-1,f(x+1)-f(x)=2x+2,求f(x).变式:f(x)是二次函数,且,f(2x+1)+f(2x-1)=16x 2-4x+6,求f(x).3、拼凑法：已知f[ g（x）]的解析式，要求f（x）时，可从f[ g（x）]的解析式中拼凑出“g（x）”，即用g（x）来表示，在将解析式的两边的g（x）用x代替即可。4、换元法：令t=g（x），在求出f（t）的解析式，然后用x代替f[ g（x）]=F（x）的两边所有的t即可。例4:已知 求变式:已知 求5、方程组法：例5已知
求f(x)变式:已知 求我们学习了求函数解析式的五常用方法:1、代入法：5、方程组法：例5已知
求f(x)2、代定系数法：已知f（x）的函数类型，要求f（x）的解析式时，可根据类型设其解析式，从而确定其系数。3、拼凑法：已知f[ g（x）]的解析式，要求f（x）时，可从f[ g（x）]的解析式中拼凑出“g（x）”，即用g（x）来表示，在将解析式的两边的g（x）用x代替即可。4、换元法：令t=g（x），在求出f（t）的解析式，然后用x代替f[ g（x）]=F（x）的两边所有的t即可。