指数函数1[上学期]
图片预览







文档简介
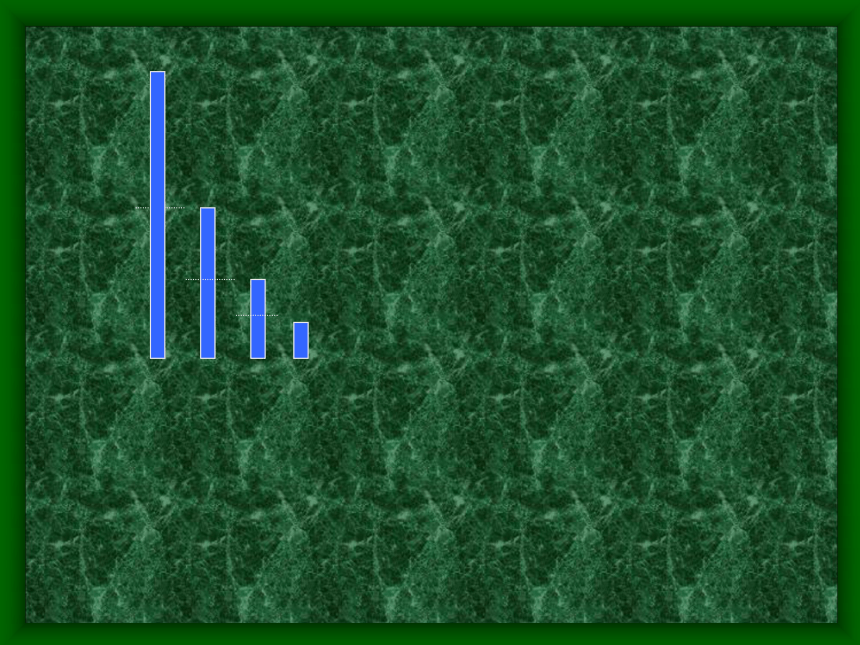
课件21张PPT。指数函数整数a的无理指数幂有意义。复习:n个把一页纸对折剪开,再合起来对折剪开,再一次合起来对折剪开,…依次下去歼的次数与纸的页数有什么关系?问题指数函数一页纸剪切x次后,得到的纸的页数y与 x的函数关系式是
y=2 x我们可以看到每剪一次后纸的页数都增加为前一次的二倍,指数函数 次数 页数1次 2 页2次 2×2=2 2 页3次 2 2 ×2=2 3 页4次 2 3×2=2 4页
…………自变量x作为指数,底数2是一个大于0而不等于1的常量x次 2 (x-1) ×2=2x页指数函数问题:一把尺子第一次截去它的一半,第二次截去剩余部分的一半,第三次截去第二次剩余部分的一半,依次截下去,问截的次数与剩下的尺子之间的关系.指数函数 次数 长度 1次 2次 我们可以看到每截一次后尺的长度都减为前一次的二分之一倍, 3次 4次 ……一把尺子截x次后,得到的尺的长度y与x的函数关系式是
自变量x作为指数,底数 是一个大于0且小于1的常量。x次一般的,函数 y = a x (a>0,a≠1)叫做指数函数,其中x是自变量。
指数函数函数的定义域是R我们要求 a>0,a≠1 是因为:(3)如果a =1, 1 x=1是一个常量,对它研究没价值。(2) 如果a <0,x = , x = 时,函数值在实数范
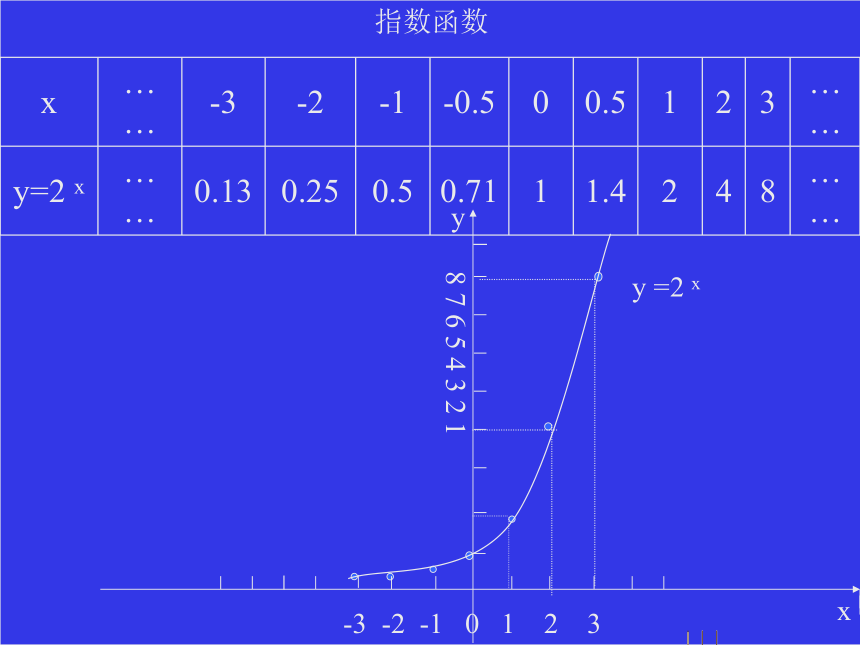
围内不存在.指数函数作出函数 y =2x 的图象:y =2 x指数函数作出函数 的图象指数函数指数函数练习:在同一坐标系作出下列函数的图象.
(1) y =10 x. (2) y =10 x指数函数图象特征函数性质(1)图象都位于X轴上方(1)x取任何实数都有ax>0.(2)这些图象都过(0,1 )点.(2)只要a >0,a≠1,总有a0 =1(3) 图象Ⅰ,Ⅱ在第一象限大于1, 在第二象限小于1;而 图象Ⅲ,Ⅳ则反之.(4)自左向右,图象Ⅰ, Ⅱ逐渐上升;图象Ⅲ, Ⅳ逐渐下降.指数函数y =3 x(0,1)0 (1) 定义域 : R指数函数在底数a>1及0< a< 1,这两种情况下的图象和性质如下:指数函数a > 10< a < 1 图 象 性 质(2)值域: ( 0 ,+∞ )(3)过点(0,1),即x=0时,y=1(4) 在R上是增函数(4)在R上是减函数练习:指数函数判断下列函数的定义域和值域.例题、已知指数函数f(x)=ax (a>0,且a≠1)的图象经过点(3,π),求f(0), f(1), f(-3)的值.练习:比较下列各题中两个值的大小.1.7 2.5, 1.7 3
(2) 0.8 –0.1, 0.8 –0.2
(3) 1.7 0.3, 0.9 3.1
指数函数解:(1)考察指数 y =1.7 x.由于底数1.7>1,所以指数函数 y =1.7 x在R上是增函数.
∵2.5<3,
∴ 1.7 2.5 <1.7 3 (2) 0.8-0.1 ,0.8-0.2
考察函数 y = 0.8 x.由于底数 0.8﹤1,所以指数函数 y = 0.8 x在R上是减函数.
∵-0.1 ﹥ -0.2,
∴ 0.8 – 0.1 ﹤ 0.8 – 0.2 (3) 1.7 0.3, 0.9 3.1
由指数函数的性质知:
1.7 0.3 ﹥1.7 0 =1,
0.9 3.1 ﹤ 0.9 0 =1,
即 1.7 0.3 ﹥ 1, 0.9 3.1﹤1
∴1.7 0.3﹥ 0.9 3.1
指数函数指数函数练习:
已知下列不等式,请判断m,n的大小.
(1) 2 m ﹤2 n
(2) a m ﹥a n (0 ﹤a ﹤1)解:
(1) 考察函数 y = 2 x.由于底数2 ﹥ 1,所以指数函数 y =2 x在R上是增函数
∵ 2 m ﹤2 n ∴ m ﹤n.
(2)考察函数 y = a x.由于底数 0 ﹤a ﹤1,所以指数函数 y = a x在R上是减函数
∵ a m ﹥a n ∴ m ﹤n.
指数函数小结:一。概念:
一般的,函数 y = a x (a>0,a≠1)叫做指数函数,其中x是自变量。
二。性质:(2)值域: ( 0 ,+∞ )(3)过点(0,1),即x=0时,y=1(4)a>1 在R上是增函数0<a <1在R上是减函数(1)定义域:R。指数函数作业:
课本 78页
1. (2), (4) ;
2. (2), (4);
3.
y=2 x我们可以看到每剪一次后纸的页数都增加为前一次的二倍,指数函数 次数 页数1次 2 页2次 2×2=2 2 页3次 2 2 ×2=2 3 页4次 2 3×2=2 4页
…………自变量x作为指数,底数2是一个大于0而不等于1的常量x次 2 (x-1) ×2=2x页指数函数问题:一把尺子第一次截去它的一半,第二次截去剩余部分的一半,第三次截去第二次剩余部分的一半,依次截下去,问截的次数与剩下的尺子之间的关系.指数函数 次数 长度 1次 2次 我们可以看到每截一次后尺的长度都减为前一次的二分之一倍, 3次 4次 ……一把尺子截x次后,得到的尺的长度y与x的函数关系式是
自变量x作为指数,底数 是一个大于0且小于1的常量。x次一般的,函数 y = a x (a>0,a≠1)叫做指数函数,其中x是自变量。
指数函数函数的定义域是R我们要求 a>0,a≠1 是因为:(3)如果a =1, 1 x=1是一个常量,对它研究没价值。(2) 如果a <0,x = , x = 时,函数值在实数范
围内不存在.指数函数作出函数 y =2x 的图象:y =2 x指数函数作出函数 的图象指数函数指数函数练习:在同一坐标系作出下列函数的图象.
(1) y =10 x. (2) y =10 x指数函数图象特征函数性质(1)图象都位于X轴上方(1)x取任何实数都有ax>0.(2)这些图象都过(0,1 )点.(2)只要a >0,a≠1,总有a0 =1(3) 图象Ⅰ,Ⅱ在第一象限大于1, 在第二象限小于1;而 图象Ⅲ,Ⅳ则反之.(4)自左向右,图象Ⅰ, Ⅱ逐渐上升;图象Ⅲ, Ⅳ逐渐下降.指数函数y =3 x(0,1)0 (1) 定义域 : R指数函数在底数a>1及0< a< 1,这两种情况下的图象和性质如下:指数函数a > 10< a < 1 图 象 性 质(2)值域: ( 0 ,+∞ )(3)过点(0,1),即x=0时,y=1(4) 在R上是增函数(4)在R上是减函数练习:指数函数判断下列函数的定义域和值域.例题、已知指数函数f(x)=ax (a>0,且a≠1)的图象经过点(3,π),求f(0), f(1), f(-3)的值.练习:比较下列各题中两个值的大小.1.7 2.5, 1.7 3
(2) 0.8 –0.1, 0.8 –0.2
(3) 1.7 0.3, 0.9 3.1
指数函数解:(1)考察指数 y =1.7 x.由于底数1.7>1,所以指数函数 y =1.7 x在R上是增函数.
∵2.5<3,
∴ 1.7 2.5 <1.7 3 (2) 0.8-0.1 ,0.8-0.2
考察函数 y = 0.8 x.由于底数 0.8﹤1,所以指数函数 y = 0.8 x在R上是减函数.
∵-0.1 ﹥ -0.2,
∴ 0.8 – 0.1 ﹤ 0.8 – 0.2 (3) 1.7 0.3, 0.9 3.1
由指数函数的性质知:
1.7 0.3 ﹥1.7 0 =1,
0.9 3.1 ﹤ 0.9 0 =1,
即 1.7 0.3 ﹥ 1, 0.9 3.1﹤1
∴1.7 0.3﹥ 0.9 3.1
指数函数指数函数练习:
已知下列不等式,请判断m,n的大小.
(1) 2 m ﹤2 n
(2) a m ﹥a n (0 ﹤a ﹤1)解:
(1) 考察函数 y = 2 x.由于底数2 ﹥ 1,所以指数函数 y =2 x在R上是增函数
∵ 2 m ﹤2 n ∴ m ﹤n.
(2)考察函数 y = a x.由于底数 0 ﹤a ﹤1,所以指数函数 y = a x在R上是减函数
∵ a m ﹥a n ∴ m ﹤n.
指数函数小结:一。概念:
一般的,函数 y = a x (a>0,a≠1)叫做指数函数,其中x是自变量。
二。性质:(2)值域: ( 0 ,+∞ )(3)过点(0,1),即x=0时,y=1(4)a>1 在R上是增函数0<a <1在R上是减函数(1)定义域:R。指数函数作业:
课本 78页
1. (2), (4) ;
2. (2), (4);
3.
