二次函数在区间上的最值问题

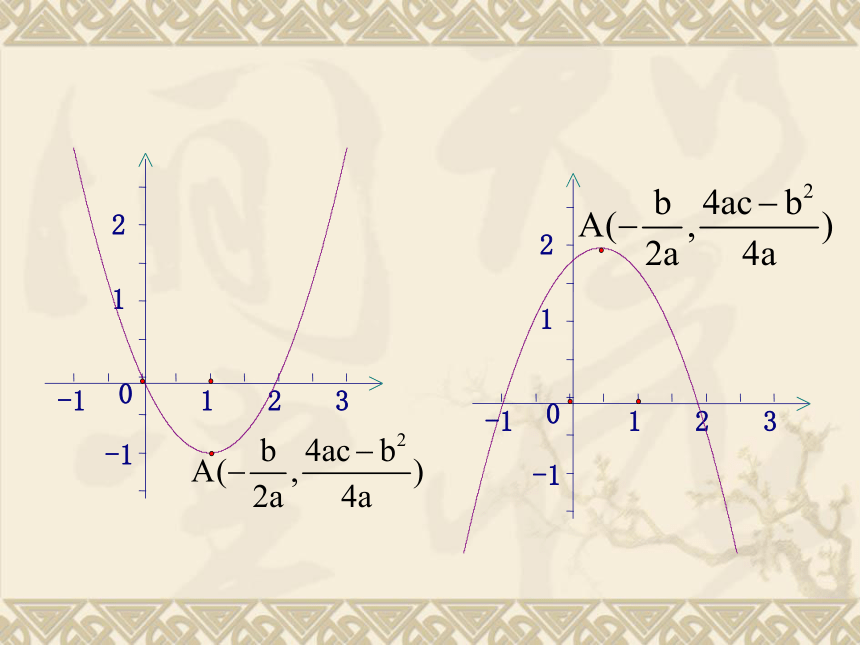
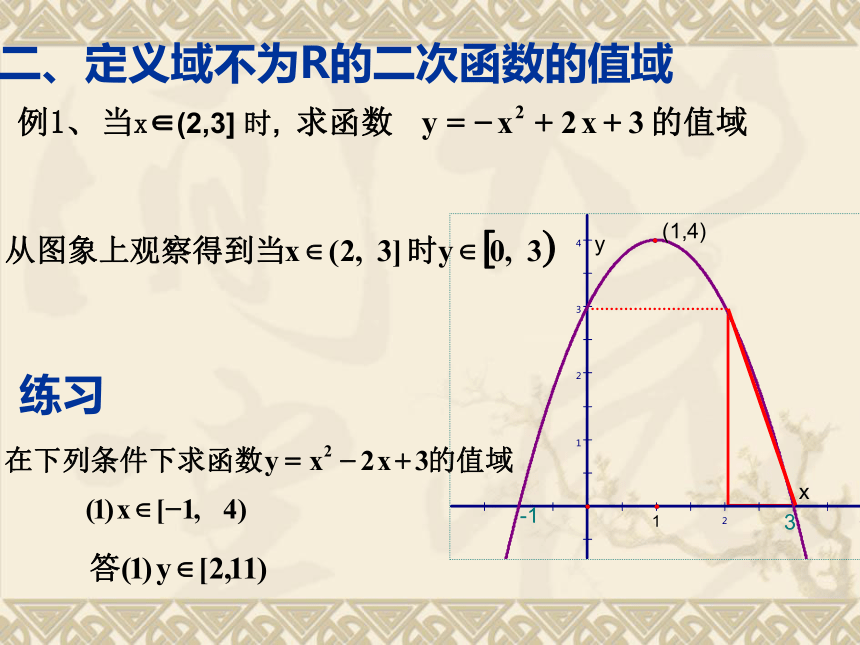
课件13张PPT。二次函数在区间上的最值问题一、定义域为R的二次函数的值域另外也可以从函数的图象上去理解。21-121-13021-121-130二、定义域不为R的二次函数的值域练习解:函数图象的对称轴为直线x=1,抛物线开口向上例2 求函数y=x2-2x+3在区间[0，a]上的最
值，并求此时x的值。
∴当x=0时，ymax=3
当x=a时，ymin=a2-2a+3
1.当0 ∴当x=0时，ymax=3
当x=a时，ymin=a2-2a+3
,函数在[0,1]上单
调递减,在[1,a]上单调递增,
∴当x=1时,ymin=2
当x=0时，ymax=3解:函数图象的对称轴为直线x=1,抛物线开口向上例2 求函数y=x2-2x+3在区间[0，a]上的最
值，并求此时x的值。2.当1 递减,在[1，a]上单调递增,
∴当x=1时,ymin=2,
当x=a时,ymax= a2-2a+3例2 求函数y=x2-2x+3在区间[0，a]上的最
值，并求此时x的值。3.当a≥2时2.当1 调递减,在[1,a]上单调递增,
∴当x=1时,ymin=2;当x=0时，ymax=3解:函数图象的对称轴为直线x=1,抛物线开口向上1.当a≤1时，函数在[0，a]上单调递减，∴当x=0时，ymax=3;当x=a时，ymin=a2-2a+3四、动函数定区间的二次函数的值域 例3、求 在 上的最值。1、由图（1）得：
当 ，即 时， 例3、求 在 上的最值。3、由图（3）得：
当 ，即 时，4、由图（4）得：
当 ，即 时，0例4 求函数y=-x(x-a)在x∈[-1,a]上的最大值解:函数图象的对称轴方程为x= ,又x∈[-1,a]故a>-1, > - ,∴对称轴在x= - 的右边.∴(1)当 -1< ≤a时,即a≥0时,由二次函数图象可知: ymax =f ( )= 五、动函数动区间的二次函数的值域(2)当a< 时,即-1 综上所述:当-1 当 a≥0时,ymax = 例4 求函数y=-x(x-a)在x∈[-1,a]上的最大值(2)当a< 时,即-1 由二次函数的图象可知:
ymax =f (a)=0课堂小结：对于求有限闭区间上的二次函数的最值问题，关键抓住二次函数图象的开口方向，对称轴及定义区间，应用数形结合法求解。
思考讨论：