平行线等分线段定理
图片预览


文档简介
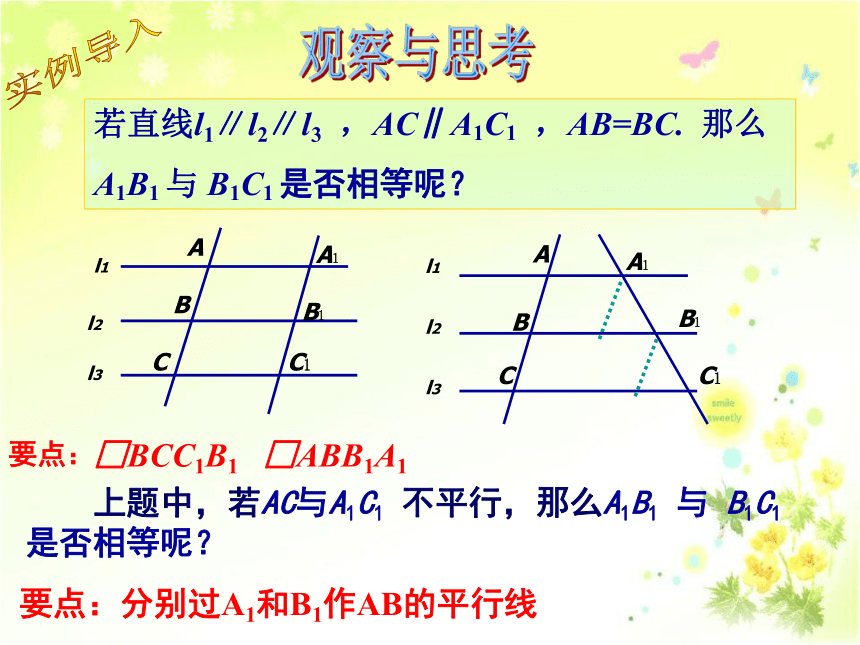
课件14张PPT。普通高中课程标准《数学选修4-1》第一讲知识与技能:1. 掌握平行线等分线段定理以及推论;2.会用以上结论等分线段以及证明一些简单的几何问题.方法与过程: 通过具体实例 ,引导学生从考察特殊情况入手,进而得到一般的结论的推理方法(归纳),从中体会从特殊到一般的数学思想方法. 教学目标若直线l1∥l2∥l3 ,AC∥A1C1 ,AB=BC. 那么
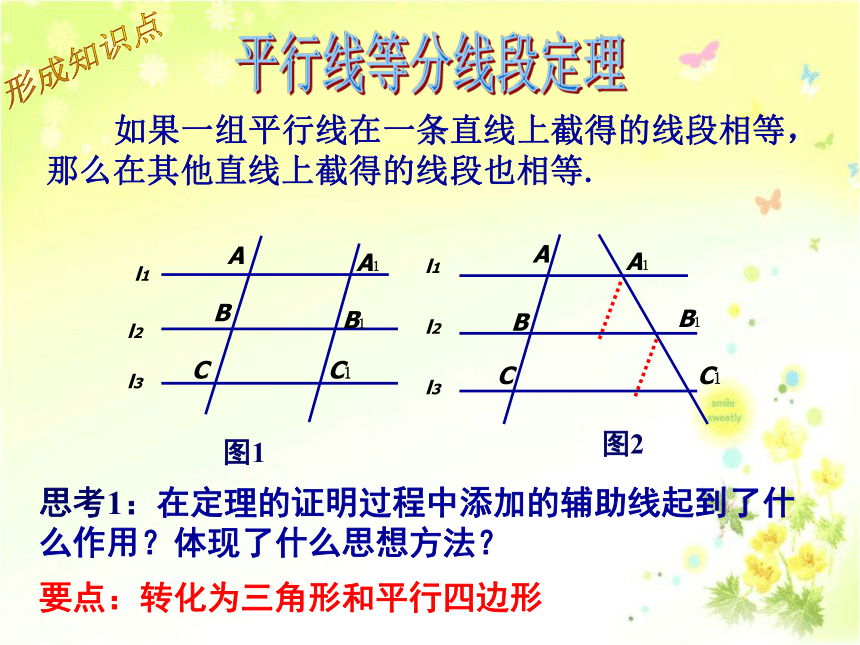
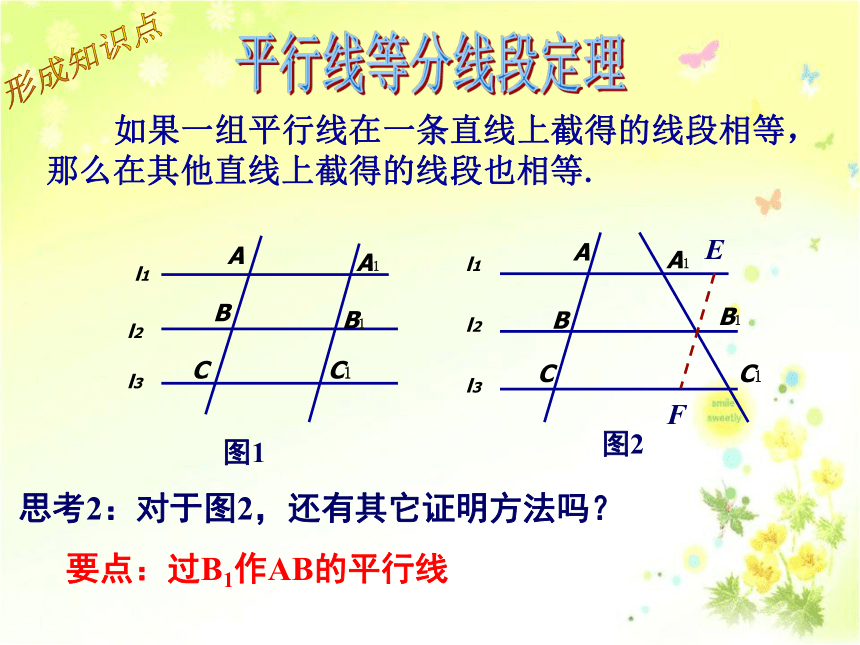
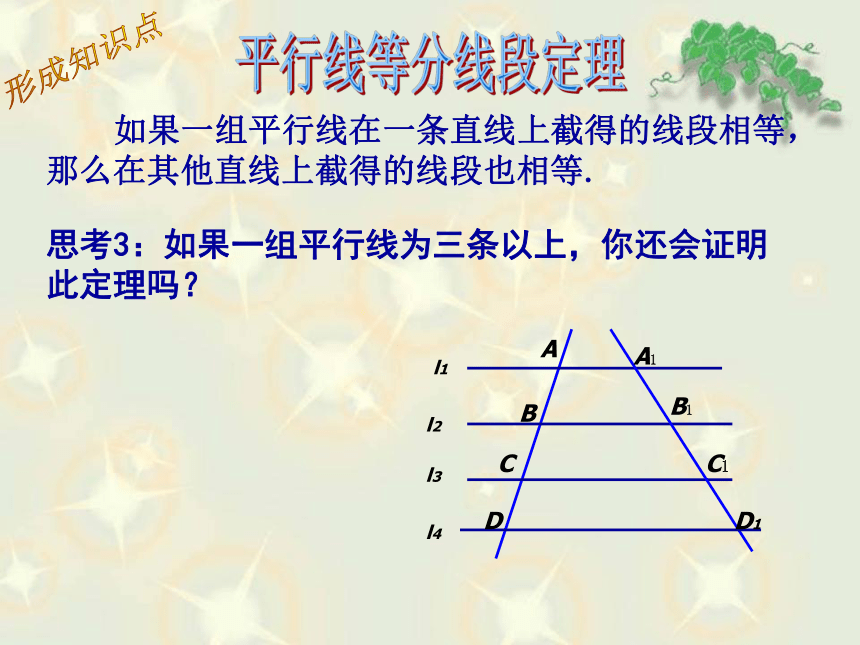
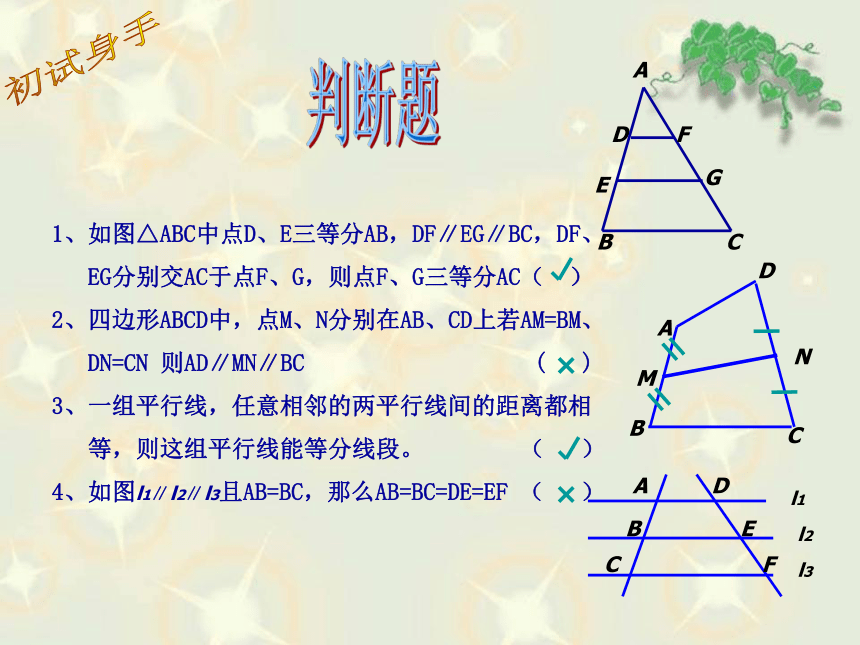
A1B1 与 B1C1 是否相等呢?实例导入观察与思考 上题中,若AC与A1C1 不平行,那么A1B1 与 B1C1 是否相等呢?要点:分别过A1和B1作AB的平行线 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理图1图2形成知识点思考1:在定理的证明过程中添加的辅助线起到了什么作用?体现了什么思想方法?要点:转化为三角形和平行四边形 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理图1图2形成知识点思考2:对于图2,还有其它证明方法吗?要点:过B1作AB的平行线思考3:如果一组平行线为三条以上,你还会证明此定理吗?形成知识点 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理ABCA1B1C1DD1l1l3l2l41、如图△ABC中点D、E三等分AB,DF∥EG∥BC,DF、
EG分别交AC于点F、G,则点F、G三等分AC( )
2、四边形ABCD中,点M、N分别在AB、CD上若AM=BM、
DN=CN 则AD∥MN∥BC ( )
3、一组平行线,任意相邻的两平行线间的距离都相
等,则这组平行线能等分线段。 ( )
4、如图l1∥l2∥l3且AB=BC,那么AB=BC=DE=EF ( )ABCl1l3l2EFDDABCEFG初试身手判断题推论2 经过梯形一腰的中点与底平行的 直线,必平分另一腰。ABCDEF图4符号语言:
∵在梯形ABCD,AD∥EF∥BC,AE=EB
∴DF=FCAEBCF推论1 经过三角形一边的中点与另一 边平行的直线,必平分第三边。符号语言
∵△ABC中,EF∥BC,AE=EB
∴AF=FC图5 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理深入探究 已知:如图,梯形ABCD中,AD∥BC,∠ABC=90。M是CD的中点
求证:AM=BM分析:过M点作ME∥AD交AB于点E
又∵在梯形ABCD中,MD=MC
∴AE=EB易证ME是AB的垂直平分线ABCDM辅助线点滴:
有线段中点时,常过该点作平行线,构造平行线等分线段定理及推论的基本图形。
实战演练证明题利用平行线等分线段定理证明三角形中位线定理D、E 分别是△ABC中AB边和AC边的中点.
求证:DE//BC且作DE?//BC作DF//AC=DE实战演练证明题已知:∠ACB=90°,AC=BC,ABC求证:MN=NB.分析:
若结论成立,则过B作NC
的平行线交直线AC必截得
相等的线段,反之亦然.∟EFMN∟∟CE=CF,EM⊥AF,CN⊥AF,实战演练证明题 如图:有块直角三角形菜地,分配给张、王、李三家农民耕种,已知张、王、李三家人口分别为2人、4人、6人,菜地分配方法按人口比例,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P 必须是三家地的交界地
要求:用尺规在图中作出各家菜地的分界应用题学以致用课堂小结1、平行线等分线段定理和两个推论2、定理和推论的应用(1)把线段n等分
(2)证明在同一直线上的线段相等3.数学思想方法
转化与化归思想、特殊与一般思想作业:P5 习题1.1 2,3
A1B1 与 B1C1 是否相等呢?实例导入观察与思考 上题中,若AC与A1C1 不平行,那么A1B1 与 B1C1 是否相等呢?要点:分别过A1和B1作AB的平行线 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理图1图2形成知识点思考1:在定理的证明过程中添加的辅助线起到了什么作用?体现了什么思想方法?要点:转化为三角形和平行四边形 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理图1图2形成知识点思考2:对于图2,还有其它证明方法吗?要点:过B1作AB的平行线思考3:如果一组平行线为三条以上,你还会证明此定理吗?形成知识点 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理ABCA1B1C1DD1l1l3l2l41、如图△ABC中点D、E三等分AB,DF∥EG∥BC,DF、
EG分别交AC于点F、G,则点F、G三等分AC( )
2、四边形ABCD中,点M、N分别在AB、CD上若AM=BM、
DN=CN 则AD∥MN∥BC ( )
3、一组平行线,任意相邻的两平行线间的距离都相
等,则这组平行线能等分线段。 ( )
4、如图l1∥l2∥l3且AB=BC,那么AB=BC=DE=EF ( )ABCl1l3l2EFDDABCEFG初试身手判断题推论2 经过梯形一腰的中点与底平行的 直线,必平分另一腰。ABCDEF图4符号语言:
∵在梯形ABCD,AD∥EF∥BC,AE=EB
∴DF=FCAEBCF推论1 经过三角形一边的中点与另一 边平行的直线,必平分第三边。符号语言
∵△ABC中,EF∥BC,AE=EB
∴AF=FC图5 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.平行线等分线段定理深入探究 已知:如图,梯形ABCD中,AD∥BC,∠ABC=90。M是CD的中点
求证:AM=BM分析:过M点作ME∥AD交AB于点E
又∵在梯形ABCD中,MD=MC
∴AE=EB易证ME是AB的垂直平分线ABCDM辅助线点滴:
有线段中点时,常过该点作平行线,构造平行线等分线段定理及推论的基本图形。
实战演练证明题利用平行线等分线段定理证明三角形中位线定理D、E 分别是△ABC中AB边和AC边的中点.
求证:DE//BC且作DE?//BC作DF//AC=DE实战演练证明题已知:∠ACB=90°,AC=BC,ABC求证:MN=NB.分析:
若结论成立,则过B作NC
的平行线交直线AC必截得
相等的线段,反之亦然.∟EFMN∟∟CE=CF,EM⊥AF,CN⊥AF,实战演练证明题 如图:有块直角三角形菜地,分配给张、王、李三家农民耕种,已知张、王、李三家人口分别为2人、4人、6人,菜地分配方法按人口比例,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P 必须是三家地的交界地
要求:用尺规在图中作出各家菜地的分界应用题学以致用课堂小结1、平行线等分线段定理和两个推论2、定理和推论的应用(1)把线段n等分
(2)证明在同一直线上的线段相等3.数学思想方法
转化与化归思想、特殊与一般思想作业:P5 习题1.1 2,3
