新课标北师大版六上1.5《圆的面积(一)》课件(28张PPT)
文档属性
| 名称 | 新课标北师大版六上1.5《圆的面积(一)》课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 10:58:28 | ||
图片预览






文档简介
(共28张PPT)
圆的面积(一)
北师大版六年级上册
教学目标
1.学习目标描述:了解圆的面积的含义,经历圆面积计算公式的推导过程,掌握圆面积计算公式;在探究圆面积公式的活动中,体会“化曲为直”的思想。
2.学习内容分析:圆的面积是学生了解和掌握了圆的特征,学会计算圆的周长以及学习直线围成的平面图形的面积计算方法的基础上进行教学的。由此教材在安排学习圆的面积公式时,运用了迁移和
教学目标
同化的理念,将“化曲为直”的转化思想确立为本节课的教学重点。通过一系列的活动将新的教学思想纳入到学生原有的认识结构之中,从而完成新知的构建过程。
3.学科核心素养分析:在探究新知的过程中,组织学生利用学具开展探究性的数学活动,注重知识的发现和探究过程,让学生从中获得学习数学的积极情感体验和感受数学的价值,增强学生的空间观念、空间观念和推理意识。
新知导入
1.说说什么是图形的面积?
图形所占平面的大小叫做图形的面积。
新知导入
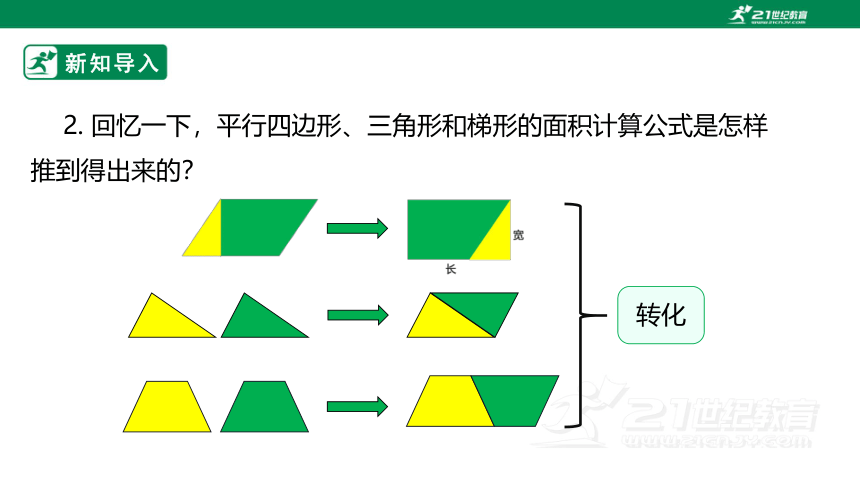
2. 回忆一下,平行四边形、三角形和梯形的面积计算公式是怎样推到得出来的?
转化
新知导入
猜
一
猜
小小圆形运动场,
三个选手比赛忙,
跑的路程分长短,
最后时间一个样。
(打一物品)
新知导入
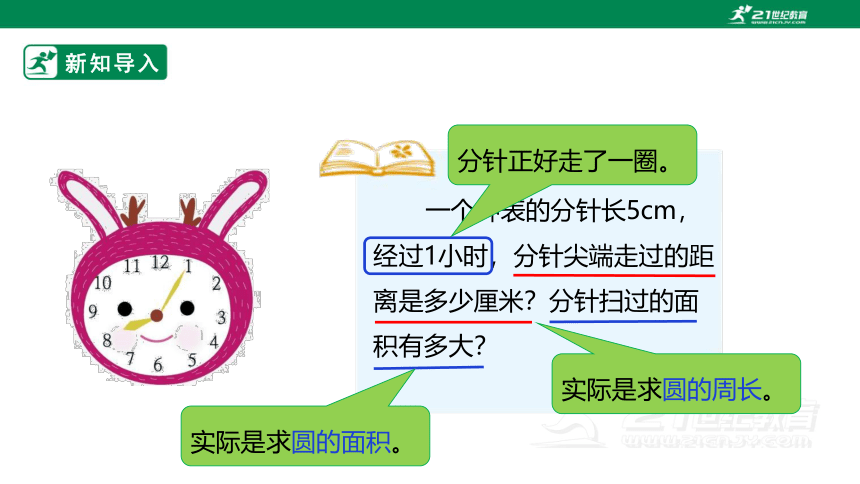
一个钟表的分针长5cm,经过1小时,分针尖端走过的距离是多少厘米?分针扫过的面积有多大?
分针正好走了一圈。
实际是求圆的周长。
实际是求圆的面积。
新知讲解
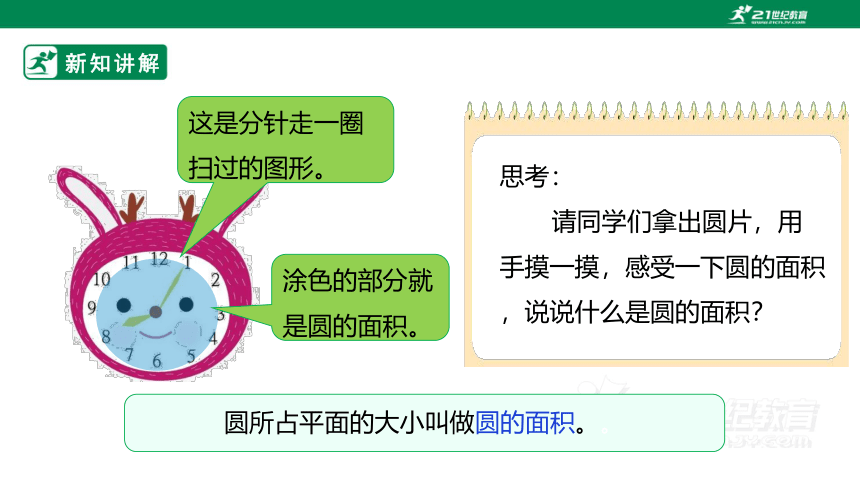
这是分针走一圈扫过的图形。
涂色的部分就是圆的面积。
思考:
请同学们拿出圆片,用手摸一摸,感受一下圆的面积,说说什么是圆的面积?
圆所占平面的大小叫做圆的面积。。
新知讲解
思考:
如何得到一个圆的面积呢?想一想,并与同伴交流。
新知讲解
在圆中画出一个最大的正方形。
我能求出正方形的面积,剩余的面积怎么办呢?
新知讲解
画方格数一数。
不是整格的怎么办呢?
新知讲解
思考:
能否将圆转化成以前学过的图形?
新知讲解
是扇形。
分成8等份
拼成了一个像平行四边形的图形。
形状像,但是两条底边不是直的。
新知讲解
分成16等份
可以近似看成平行四边形。
新知讲解
想一想,圆等分的份数越多,拼出的图形就越接近什么形状?
分成32等份
更行四边形。
新知讲解
思考提示:
1.圆的面积与平行四边形的面积有什么关系?
2.平行四边形的底相当于圆的什么?平行四边形的高呢?
3.你能平行四边形的面积推导出圆的面积公式吗?
拼成的平行四边形与原来的圆之间有什么联系呢?
新知讲解
圆的面积
平行四边形的面积
= 底 × 高
圆周长的一半
= ×
半径
圆周长的一半
半径
如果用S表示圆的面积,r表示圆的半径,那么:
S = πr × r
= πr2
新知讲解
一个钟表的分针长5cm,经过1小时,分针尖端走过的距离是多少厘米?分针扫过的面积有多大?
3.14×5×2=31.4(厘米)
3.14×52=78.5(平方厘米)
答:分针尖端走过的距离是31.4厘米,分针扫过的面积是78.5平方厘米。
课堂练习
1.填一填。
把一个圆平均分成若干份,拼成的图形越行四边形,平行四边形的底相当于( ),高相当于( ),圆的面积S=( )。
圆周长的一半
圆的半径
πr2
课堂练习
2.判断。
(1)半径是4厘米的圆,周长比面积大。 ( )
(2)半径是5厘米的圆与直径是10厘米的圆的大小相等。 ( )
(3)一个圆平均分的份数越多,所拼成的图形越行四边形。
( )
×
周长与面积是两个不同的范畴。
半径是5厘米
√
√
课堂练习
3.利用圆的面积公式尝试求出圆的面积。
4cm
5dm
3.14×42=50.24(cm2)
3.14×52=78.5(dm2)
课堂练习
4.拓展应用:正方形的面积是4厘米,那么这个圆的面积是多少?
正方形的边长等于圆的半径,所以r2=4。
3.14×4=12.56(cm2)
答:这个圆的面积是12.56cm2。
课堂练习
12~102π的倍数表格
12π=3.14 22π=12.56 32π =28.26 42π =50.24 52π =78.5
62π =113.04 72π =153.86 82π =200.96 92π =254.34 102π =314
记一记
课堂总结
通过今天的学习,你有哪些收获?
我知道圆的面积S=πr2。
我还知道把圆平均分成若干份,可以拼组成近似的平行四边形。
板书设计
圆的面积(一)
圆的面积
平行四边形的面积
= 底 × 高
= ×
圆周长的一半
半径
S = πr × r
= πr2
作业布置
完成课本“练一练”第1、2、3题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
圆的面积(一)
北师大版六年级上册
教学目标
1.学习目标描述:了解圆的面积的含义,经历圆面积计算公式的推导过程,掌握圆面积计算公式;在探究圆面积公式的活动中,体会“化曲为直”的思想。
2.学习内容分析:圆的面积是学生了解和掌握了圆的特征,学会计算圆的周长以及学习直线围成的平面图形的面积计算方法的基础上进行教学的。由此教材在安排学习圆的面积公式时,运用了迁移和
教学目标
同化的理念,将“化曲为直”的转化思想确立为本节课的教学重点。通过一系列的活动将新的教学思想纳入到学生原有的认识结构之中,从而完成新知的构建过程。
3.学科核心素养分析:在探究新知的过程中,组织学生利用学具开展探究性的数学活动,注重知识的发现和探究过程,让学生从中获得学习数学的积极情感体验和感受数学的价值,增强学生的空间观念、空间观念和推理意识。
新知导入
1.说说什么是图形的面积?
图形所占平面的大小叫做图形的面积。
新知导入
2. 回忆一下,平行四边形、三角形和梯形的面积计算公式是怎样推到得出来的?
转化
新知导入
猜
一
猜
小小圆形运动场,
三个选手比赛忙,
跑的路程分长短,
最后时间一个样。
(打一物品)
新知导入
一个钟表的分针长5cm,经过1小时,分针尖端走过的距离是多少厘米?分针扫过的面积有多大?
分针正好走了一圈。
实际是求圆的周长。
实际是求圆的面积。
新知讲解
这是分针走一圈扫过的图形。
涂色的部分就是圆的面积。
思考:
请同学们拿出圆片,用手摸一摸,感受一下圆的面积,说说什么是圆的面积?
圆所占平面的大小叫做圆的面积。。
新知讲解
思考:
如何得到一个圆的面积呢?想一想,并与同伴交流。
新知讲解
在圆中画出一个最大的正方形。
我能求出正方形的面积,剩余的面积怎么办呢?
新知讲解
画方格数一数。
不是整格的怎么办呢?
新知讲解
思考:
能否将圆转化成以前学过的图形?
新知讲解
是扇形。
分成8等份
拼成了一个像平行四边形的图形。
形状像,但是两条底边不是直的。
新知讲解
分成16等份
可以近似看成平行四边形。
新知讲解
想一想,圆等分的份数越多,拼出的图形就越接近什么形状?
分成32等份
更行四边形。
新知讲解
思考提示:
1.圆的面积与平行四边形的面积有什么关系?
2.平行四边形的底相当于圆的什么?平行四边形的高呢?
3.你能平行四边形的面积推导出圆的面积公式吗?
拼成的平行四边形与原来的圆之间有什么联系呢?
新知讲解
圆的面积
平行四边形的面积
= 底 × 高
圆周长的一半
= ×
半径
圆周长的一半
半径
如果用S表示圆的面积,r表示圆的半径,那么:
S = πr × r
= πr2
新知讲解
一个钟表的分针长5cm,经过1小时,分针尖端走过的距离是多少厘米?分针扫过的面积有多大?
3.14×5×2=31.4(厘米)
3.14×52=78.5(平方厘米)
答:分针尖端走过的距离是31.4厘米,分针扫过的面积是78.5平方厘米。
课堂练习
1.填一填。
把一个圆平均分成若干份,拼成的图形越行四边形,平行四边形的底相当于( ),高相当于( ),圆的面积S=( )。
圆周长的一半
圆的半径
πr2
课堂练习
2.判断。
(1)半径是4厘米的圆,周长比面积大。 ( )
(2)半径是5厘米的圆与直径是10厘米的圆的大小相等。 ( )
(3)一个圆平均分的份数越多,所拼成的图形越行四边形。
( )
×
周长与面积是两个不同的范畴。
半径是5厘米
√
√
课堂练习
3.利用圆的面积公式尝试求出圆的面积。
4cm
5dm
3.14×42=50.24(cm2)
3.14×52=78.5(dm2)
课堂练习
4.拓展应用:正方形的面积是4厘米,那么这个圆的面积是多少?
正方形的边长等于圆的半径,所以r2=4。
3.14×4=12.56(cm2)
答:这个圆的面积是12.56cm2。
课堂练习
12~102π的倍数表格
12π=3.14 22π=12.56 32π =28.26 42π =50.24 52π =78.5
62π =113.04 72π =153.86 82π =200.96 92π =254.34 102π =314
记一记
课堂总结
通过今天的学习,你有哪些收获?
我知道圆的面积S=πr2。
我还知道把圆平均分成若干份,可以拼组成近似的平行四边形。
板书设计
圆的面积(一)
圆的面积
平行四边形的面积
= 底 × 高
= ×
圆周长的一半
半径
S = πr × r
= πr2
作业布置
完成课本“练一练”第1、2、3题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
