24.4中位线(共2课时)
图片预览





文档简介
课件36张PPT。华东师大版
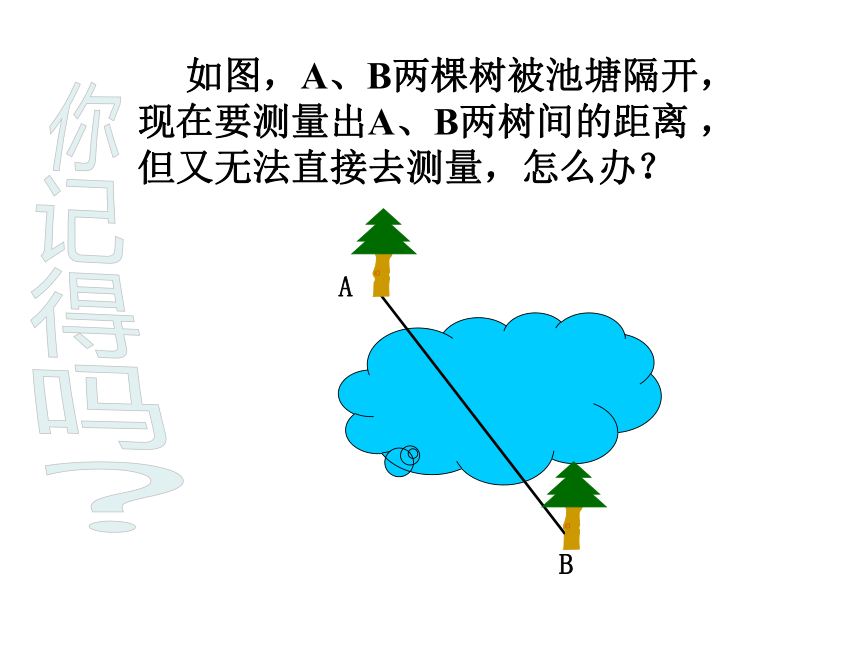
九年级(上)数学教学课件华东师大版九年级(上册)(第1课时)24.4 中位线 如图,A、B两棵树被池塘隔开,现在要测量出A、B两树间的距离 ,但又无法直接去测量,怎么办?A B。。你记得吗?A B。。C 。
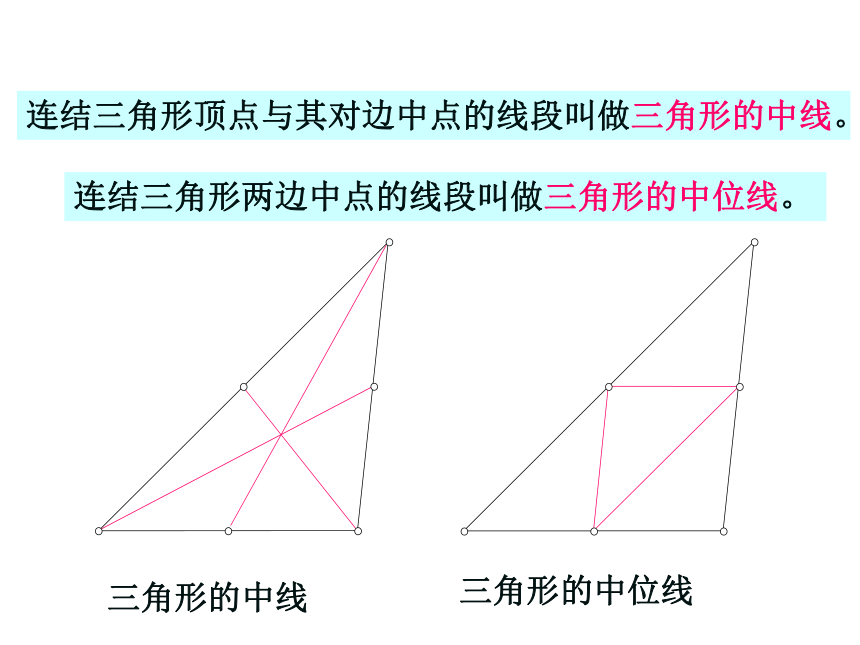
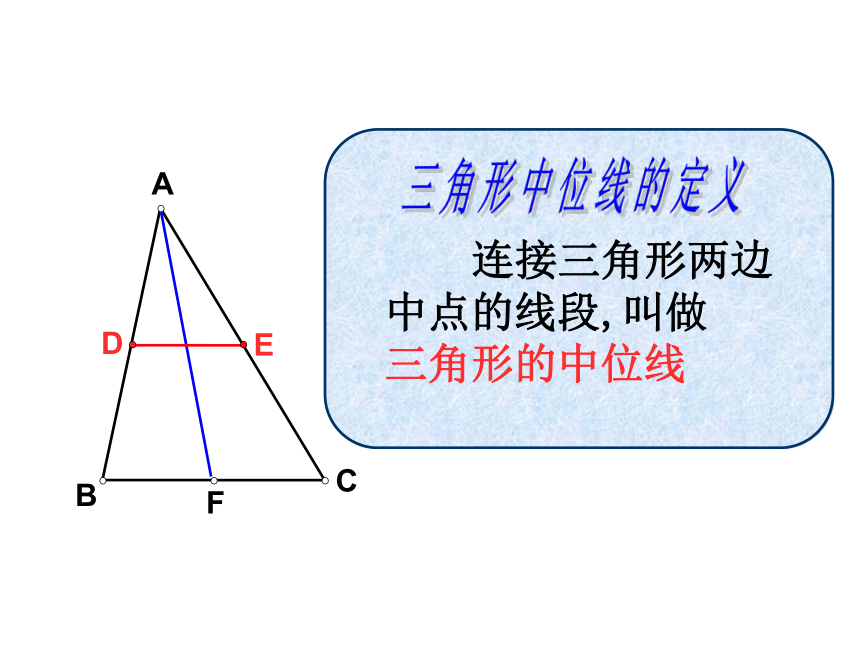
E。三角形的中线三角形的中位线连结三角形两边中点的线段叫做三角形的中位线。连结三角形顶点与其对边中点的线段叫做三角形的中线。 三角形的中位线CBAFED 连接三角形两边中点的线段,叫做 三角形的中位线
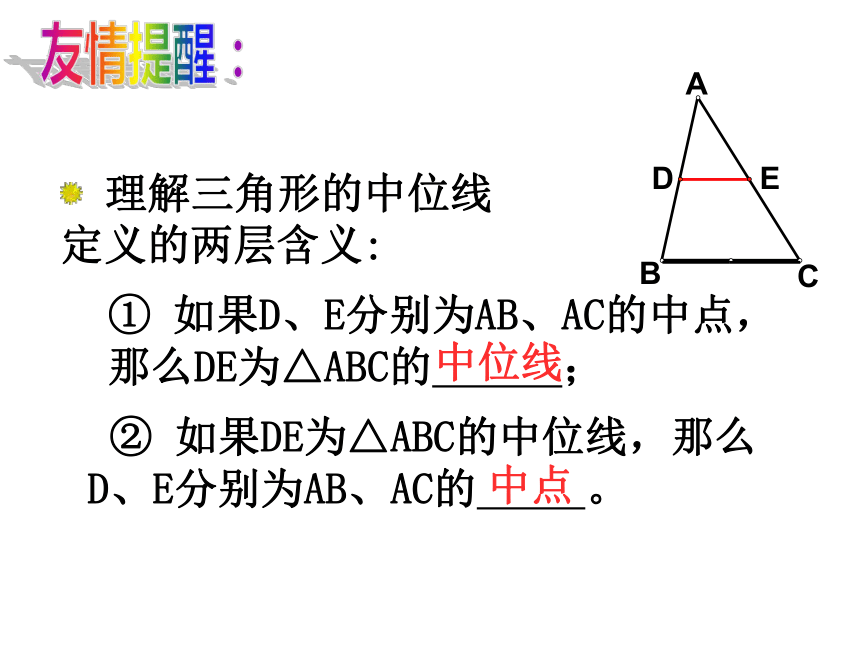
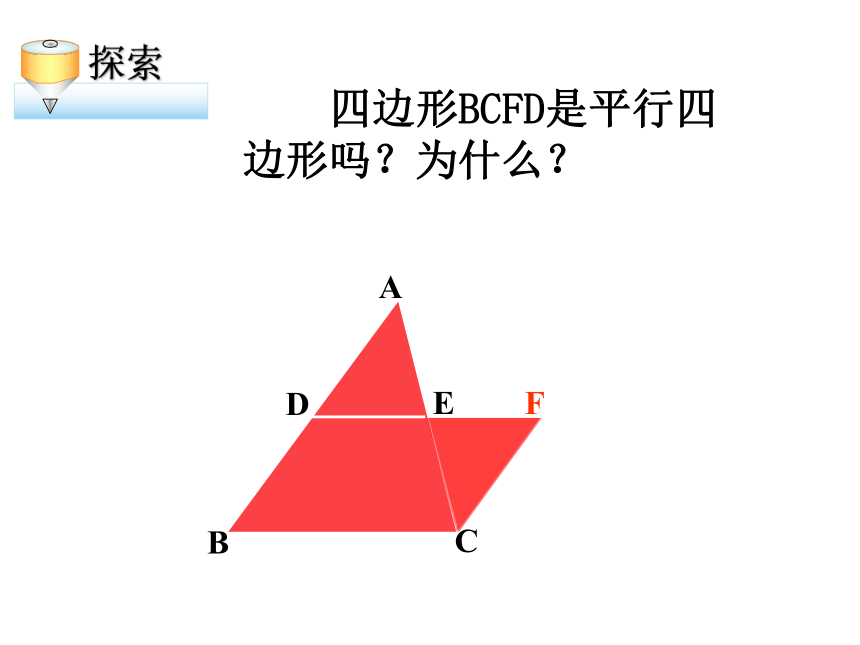
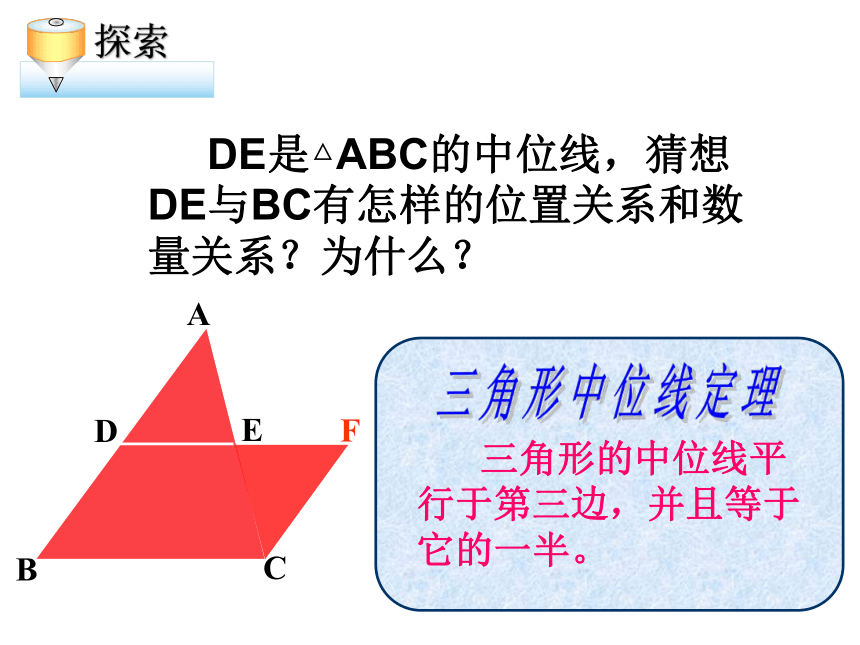
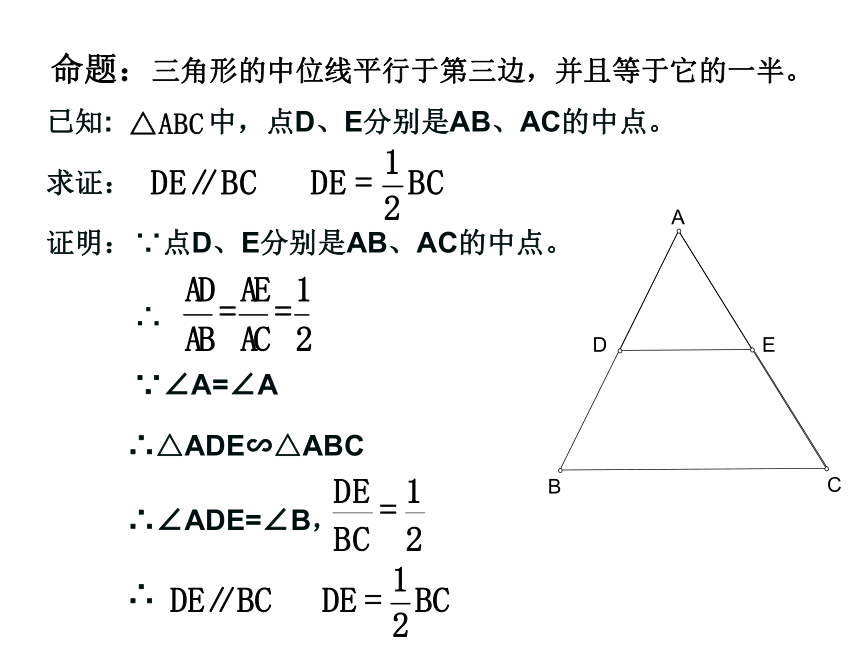
三角形中位线的定义友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点 怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?ABCDEFABCDEF 四边形BCFD是平行四边形吗?为什么? 三角形的中位线平行于第三边,并且等于它的一半。 DE是△ABC的中位线,猜想DE与BC有怎样的位置关系和数量关系?为什么?ABCDEF三角形中位线定理求证:命题:三角形的中位线平行于第三边,并且等于它的一半。已知: 中,点D、E分别是AB、AC的中点。证明:∵点D、E分别是AB、AC的中点。∴∵∠A=∠A∴△ADE∽△ABC∴∠ADE=∠B,∴三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。三角形中位线定理的数学语言表示为:
∵△ABC中,点D、E分别是AB、AC的中点。或 ∵△ABC中,AD=DB,AE=EC∴ A、B两点被池塘隔开,如何才能知道它们之间的距离呢? 在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?说一说CBA2040如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD EBACD EF543例1 求证三角形的一条中位线与第三边上的中线互相平分.已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 证明 :连结ED, ∵ D、E分别是边BC、AB的中点,∴ DE∥AC,(三角形的中位线平行于第三边并且等于第三边的一半), ∴ △ACG∽△DEG,∴ ∴ 拓展如果在图1中,取AC的中点F,假设BF与AD交于G′,如图2,那么我们
同理有 ,所以
有 ,即两图中的点G与G′是重合的. 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的
已知:△ABC中,点O为△ABC的重心。求证:证明:连接EF.∵点O为△ABC的重心,∴AE=BE,AF=CF.∴△OEF∽△OCB.∴∴求证:重心与一边中点的连线的长是对应中线长的 。∴EF∥BC,EF= BC.练 习 在△ABC中,∠BAC=90°,D、E、F分别为BC、AC、AB
的中点,AD、BE、CF相交与O点,AB=6,AC=8,试求线段
OA、OE、OF的长度。解:在Rt△ABC中,∵D为BC边上的中点∴AD= BC=5∴在Rt△ABE中,∴在Rt△AFC中,∴说一说你学到了什么?布置作业1、练习 第1题
2、习题24.4 第1题24.4中位线华东师大版九年级(上册)(第2课时)上节回顾三角形的重心:
三角形三条中线的交点。三角形的中位线:
连结三角形两边中点的线段。定理:
三角形的中位线平行于第三边,并且等于它的一半。性质:重心与一边中点的连线的长是对应
中线长的 。
探索应用 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:顺次连结四边形各边中点所得的四边形是平行四边形。 求证:四边形EFGH是平行四边形证明: 连结AC、BD∵AH=HD,CG=GD∴HG∥EF且 HG=EF∴四边形EFGH是平行四边形∴HG∥AC,同理 EF∥AC,如图所示的三角架,各横木之间互相平
行,且PA=AE=BE,PD=DF=FC.若EF=40cm,则
AD= cm.想一想:你会求BC的长吗?PAEBCDF20 新知探索 梯形的中位线定义: 连结梯形两腰中点的线段叫做梯形的中位线。 新知介绍 做一做:
1.画一个梯形ABCD,使AD∥BC;
2.分别取AB、CD的中点E、F,连接EF;
3.沿AF将梯形分成两部分,并画出将△AFD
绕点F旋转180°后的图形.ABCDEFM 新知探索 梯形中位线性质定理 梯形的中位线平行于两底,并且等于两底和的一半。如图,在梯形ABCD中,AD∥BC,
如果AE=EB,DF=FC ,那么EF∥AD∥BC,梯形中位线定理的数学语言表示为: EF= (AD+BC)已知:如图,在梯形ABCD中,AD∥BC,AE=BE,DF=CF求证:EF∥BC,证明:连结AF并延长与BC的延长线
交于点G则AD∥CG∴∠D=∠DCG∵∠AFD=∠CFG,DF=CF∴△ADF≌△GCF∴AF=FG,AD=CG∵AE=BE∴EF∥BC,∵BG=BC+CG∴例 如图所示的梯形梯子,AA′∥EE′, AB=BC=CD=DE,A′B′= B′C′= C′D′= D′E′, AA′=40cm, EE′=80cm.
求 : BB′、CC ′、DD′.AEA′E′BCDB′C′D′ 例题巩固 试一试:
如图所示的三角架,各横木之间互相平
行,且PA=AE=BE,PD=DF=FC.若EF=40cm,则
AD= cm.
想一想:你会求BC的长吗?PAEBCDF20 解决问题 练一练: (一)
1.(1)梯形的上底长4cm,下底长6cm,则
中位线长 cm.
(2)梯形上底长6cm,中位线长8cm,则下
底长 cm.
(3)等腰梯形的中位线长6cm,腰长5cm,
则梯形的周长是 cm.
(4)若梯形的中位线长6cm,高为5cm,
你会求梯形的面积吗?(5)一个等腰梯形的周长为80cm,如果
中位线长与腰长相等,高为12cm,求梯形
的面积.例 如图,在直角梯形ABCD中,点O为CD
的中点.
(1)度量顶点A、B到点O的距离,你有什么
发现?
(2)你的结论正确吗?说明理由.·OABCD·E 例题巩固 练一练: (二)
如图,梯形ABCD中,AD∥BC, E是腰AB的中
点,且DE⊥CE. 你能说明 DC=AD+CB吗?
试试看.梯形的中位线:连结梯形两腰中点的线段。 性质定理:梯形的中位线平行于两底边,并且等于
两底和的一半。 本节课我们学习了哪些内容?
九年级(上)数学教学课件华东师大版九年级(上册)(第1课时)24.4 中位线 如图,A、B两棵树被池塘隔开,现在要测量出A、B两树间的距离 ,但又无法直接去测量,怎么办?A B。。你记得吗?A B。。C 。
E。三角形的中线三角形的中位线连结三角形两边中点的线段叫做三角形的中位线。连结三角形顶点与其对边中点的线段叫做三角形的中线。 三角形的中位线CBAFED 连接三角形两边中点的线段,叫做 三角形的中位线
三角形中位线的定义友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点 怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?ABCDEFABCDEF 四边形BCFD是平行四边形吗?为什么? 三角形的中位线平行于第三边,并且等于它的一半。 DE是△ABC的中位线,猜想DE与BC有怎样的位置关系和数量关系?为什么?ABCDEF三角形中位线定理求证:命题:三角形的中位线平行于第三边,并且等于它的一半。已知: 中,点D、E分别是AB、AC的中点。证明:∵点D、E分别是AB、AC的中点。∴∵∠A=∠A∴△ADE∽△ABC∴∠ADE=∠B,∴三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。三角形中位线定理的数学语言表示为:
∵△ABC中,点D、E分别是AB、AC的中点。或 ∵△ABC中,AD=DB,AE=EC∴ A、B两点被池塘隔开,如何才能知道它们之间的距离呢? 在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?说一说CBA2040如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD EBACD EF543例1 求证三角形的一条中位线与第三边上的中线互相平分.已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 证明 :连结ED, ∵ D、E分别是边BC、AB的中点,∴ DE∥AC,(三角形的中位线平行于第三边并且等于第三边的一半), ∴ △ACG∽△DEG,∴ ∴ 拓展如果在图1中,取AC的中点F,假设BF与AD交于G′,如图2,那么我们
同理有 ,所以
有 ,即两图中的点G与G′是重合的. 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的
已知:△ABC中,点O为△ABC的重心。求证:证明:连接EF.∵点O为△ABC的重心,∴AE=BE,AF=CF.∴△OEF∽△OCB.∴∴求证:重心与一边中点的连线的长是对应中线长的 。∴EF∥BC,EF= BC.练 习 在△ABC中,∠BAC=90°,D、E、F分别为BC、AC、AB
的中点,AD、BE、CF相交与O点,AB=6,AC=8,试求线段
OA、OE、OF的长度。解:在Rt△ABC中,∵D为BC边上的中点∴AD= BC=5∴在Rt△ABE中,∴在Rt△AFC中,∴说一说你学到了什么?布置作业1、练习 第1题
2、习题24.4 第1题24.4中位线华东师大版九年级(上册)(第2课时)上节回顾三角形的重心:
三角形三条中线的交点。三角形的中位线:
连结三角形两边中点的线段。定理:
三角形的中位线平行于第三边,并且等于它的一半。性质:重心与一边中点的连线的长是对应
中线长的 。
探索应用 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:顺次连结四边形各边中点所得的四边形是平行四边形。 求证:四边形EFGH是平行四边形证明: 连结AC、BD∵AH=HD,CG=GD∴HG∥EF且 HG=EF∴四边形EFGH是平行四边形∴HG∥AC,同理 EF∥AC,如图所示的三角架,各横木之间互相平
行,且PA=AE=BE,PD=DF=FC.若EF=40cm,则
AD= cm.想一想:你会求BC的长吗?PAEBCDF20 新知探索 梯形的中位线定义: 连结梯形两腰中点的线段叫做梯形的中位线。 新知介绍 做一做:
1.画一个梯形ABCD,使AD∥BC;
2.分别取AB、CD的中点E、F,连接EF;
3.沿AF将梯形分成两部分,并画出将△AFD
绕点F旋转180°后的图形.ABCDEFM 新知探索 梯形中位线性质定理 梯形的中位线平行于两底,并且等于两底和的一半。如图,在梯形ABCD中,AD∥BC,
如果AE=EB,DF=FC ,那么EF∥AD∥BC,梯形中位线定理的数学语言表示为: EF= (AD+BC)已知:如图,在梯形ABCD中,AD∥BC,AE=BE,DF=CF求证:EF∥BC,证明:连结AF并延长与BC的延长线
交于点G则AD∥CG∴∠D=∠DCG∵∠AFD=∠CFG,DF=CF∴△ADF≌△GCF∴AF=FG,AD=CG∵AE=BE∴EF∥BC,∵BG=BC+CG∴例 如图所示的梯形梯子,AA′∥EE′, AB=BC=CD=DE,A′B′= B′C′= C′D′= D′E′, AA′=40cm, EE′=80cm.
求 : BB′、CC ′、DD′.AEA′E′BCDB′C′D′ 例题巩固 试一试:
如图所示的三角架,各横木之间互相平
行,且PA=AE=BE,PD=DF=FC.若EF=40cm,则
AD= cm.
想一想:你会求BC的长吗?PAEBCDF20 解决问题 练一练: (一)
1.(1)梯形的上底长4cm,下底长6cm,则
中位线长 cm.
(2)梯形上底长6cm,中位线长8cm,则下
底长 cm.
(3)等腰梯形的中位线长6cm,腰长5cm,
则梯形的周长是 cm.
(4)若梯形的中位线长6cm,高为5cm,
你会求梯形的面积吗?(5)一个等腰梯形的周长为80cm,如果
中位线长与腰长相等,高为12cm,求梯形
的面积.例 如图,在直角梯形ABCD中,点O为CD
的中点.
(1)度量顶点A、B到点O的距离,你有什么
发现?
(2)你的结论正确吗?说明理由.·OABCD·E 例题巩固 练一练: (二)
如图,梯形ABCD中,AD∥BC, E是腰AB的中
点,且DE⊥CE. 你能说明 DC=AD+CB吗?
试试看.梯形的中位线:连结梯形两腰中点的线段。 性质定理:梯形的中位线平行于两底边,并且等于
两底和的一半。 本节课我们学习了哪些内容?
