《对数函数及其性质》第一课时(步一隽)[上学期]
文档属性
| 名称 | 《对数函数及其性质》第一课时(步一隽)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 463.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-20 17:28:00 | ||
图片预览






文档简介
课件17张PPT。对数函数及其性质(一)杭州七中
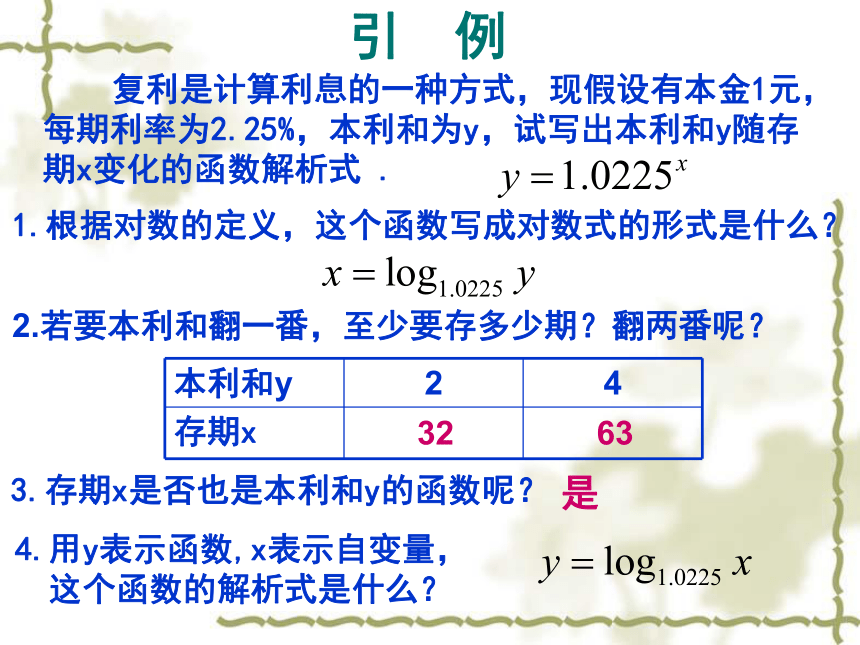
步一隽引 例 复利是计算利息的一种方式,现假设有本金1元,每期利率为2.25%,本利和为y,试写出本利和y随存期x变化的函数解析式 .1.根据对数的定义,这个函数写成对数式的形式是什么?3.存期x是否也是本利和y的函数呢?4.用y表示函数,x表示自变量,
这个函数的解析式是什么? 是2.若要本利和翻一番,至少要存多少期?翻两番呢?3263对数函数的定义对数函数模型(一)火箭的最大速度v和燃料质量M、火箭质量m的函数关系是:生物学家研究发现:洄游鱼类的游速v和鱼的耗氧量O之间的函数关系:对数函数模型(二)溶液的酸碱度是通过PH值来刻画的,PH值的计算公式为:对数函数模型(三)探究对数函数1.函数图象的探究2.函数性质的归纳两类对数函数
的图象特征
和性质的分析yy(1,0)下上逐渐上升逐渐下降定义域:( 0,+∞);值域:Rloga1=0当a>1时, x∈(0,1)时,y<0
x∈(1,+∞)时,y>0
当01时,y=logax在( 0,+∞) 是增函数;
当0 所以它在(0,+∞)上是增函数,于是
log23.4<log28.5 小结:1.体现了函数思想的应用.
2.体现了分类讨论思想的应用. >练习1.已知下列不等式,比较正数m、n的大小. >>小结:1. 体现了数形结合思想的应用.
2.“介值法”体现了问题的转化思想. >>>例题与练习例二.设函数(2)若该函数的定义域为[1,3],求该函数的值域.(3)若该函数的值域为[1,3],求该函数的定义域.(1)求该函数的定义域.小结:函数思想是实现核心内涵到外延应用的途径. 1.解:要使函数有意义,则:故函数的定义域为小结:求形如 的函数定义域要考虑2.解:那么:即:故该函数的值域为思考题若函数求a的取值范围.小结1.自主探究新知识的方法:从特殊到一般,具体到抽象的归纳;知识之间的类比.
2.本课知识点.
3.实现知识内涵到外延应用的途径.对数函数y=log a x (a>0, a≠1)(4) 0 x>1时, y>0(4) 00;
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质作业1.看书P77—P79,梳理对数函数的定义、图象、性质等知识点.
2.课本P82习题2.2:(A组)7、9、10;(B组)2;
3.思考:
(1)对比指数函数和对数函数的定义、图象、性质,预习课本p80,了解反函数的概念.
(2)思考题
步一隽引 例 复利是计算利息的一种方式,现假设有本金1元,每期利率为2.25%,本利和为y,试写出本利和y随存期x变化的函数解析式 .1.根据对数的定义,这个函数写成对数式的形式是什么?3.存期x是否也是本利和y的函数呢?4.用y表示函数,x表示自变量,
这个函数的解析式是什么? 是2.若要本利和翻一番,至少要存多少期?翻两番呢?3263对数函数的定义对数函数模型(一)火箭的最大速度v和燃料质量M、火箭质量m的函数关系是:生物学家研究发现:洄游鱼类的游速v和鱼的耗氧量O之间的函数关系:对数函数模型(二)溶液的酸碱度是通过PH值来刻画的,PH值的计算公式为:对数函数模型(三)探究对数函数1.函数图象的探究2.函数性质的归纳两类对数函数
的图象特征
和性质的分析yy(1,0)下上逐渐上升逐渐下降定义域:( 0,+∞);值域:Rloga1=0当a>1时, x∈(0,1)时,y<0
x∈(1,+∞)时,y>0
当0
当0
log23.4<log28.5 小结:1.体现了函数思想的应用.
2.体现了分类讨论思想的应用. >练习1.已知下列不等式,比较正数m、n的大小. >>小结:1. 体现了数形结合思想的应用.
2.“介值法”体现了问题的转化思想. >>>例题与练习例二.设函数(2)若该函数的定义域为[1,3],求该函数的值域.(3)若该函数的值域为[1,3],求该函数的定义域.(1)求该函数的定义域.小结:函数思想是实现核心内涵到外延应用的途径. 1.解:要使函数有意义,则:故函数的定义域为小结:求形如 的函数定义域要考虑2.解:那么:即:故该函数的值域为思考题若函数求a的取值范围.小结1.自主探究新知识的方法:从特殊到一般,具体到抽象的归纳;知识之间的类比.
2.本课知识点.
3.实现知识内涵到外延应用的途径.对数函数y=log a x (a>0, a≠1)(4) 0
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质作业1.看书P77—P79,梳理对数函数的定义、图象、性质等知识点.
2.课本P82习题2.2:(A组)7、9、10;(B组)2;
3.思考:
(1)对比指数函数和对数函数的定义、图象、性质,预习课本p80,了解反函数的概念.
(2)思考题
