苏科版七年级上册数学 3.3代数式的值 教案
文档属性
| 名称 | 苏科版七年级上册数学 3.3代数式的值 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 07:56:45 | ||
图片预览

文档简介
3.3代数式的值
【教学目标】
知识与能力:1.能读懂计算程序图(框图),会按照规定的程序计算代数式的值。
2.会按照要求设计简单的计算程序,初步感受“算法”的思想。
过程与方法:1.经历探索按程序求值的过程。
2.经历探索已知代数式写出程序的过程,感悟互逆的思维活动。
情感、态度与价值观:通过使学生明白数学来源于生活,学习数学是为了解决实际问题,培养学生科学的学习态度。
【教学重点】 会按规定的程序计算代数式的值,会按要求设计简单的计算程序.
【教学难点】已知代数式,设计程序。
【教学过程】
1、回忆旧知
当x = -1时,求代数式 的值。
(设计意图:回忆代数式的值(1)的内容,再次提醒学生代数式求值的注意点,为新课服务)
2、创设情境
同学们任意说一个整数,把这个数加上5,再乘4,然后减去20,再乘以2,最后除以4,老师可以立马报出答案。你知道其中的奥秘吗?
请学生在心里想一个数,并算出结果,再把心里想的数报给老师,老师可以立马告诉大家输出的数是多少。其中有什么奥秘呢?带着这个疑问,我们来学习今天的内容。 首先我们来学习下图形符号的功能。(多媒体显示):
是输入、输出框,表示最初输入的数值和最终输出的数值;
是处理框(执行框),表示流入此框的数值要进行某种运算,并将
运算结果的数值流出;
是流程线,用来连接程序框,表示数值的流动方向
(设计意图:通过小程序调动学生学习积极性,让学生感受到数学来源生活,引
入本节课知识点并介绍图形符号的功能)
三、例题讲解
例1、按计算程序计算并填写下表:(程序-代数式-求值)
输入 -3 - -1 0 1.5 5
输出
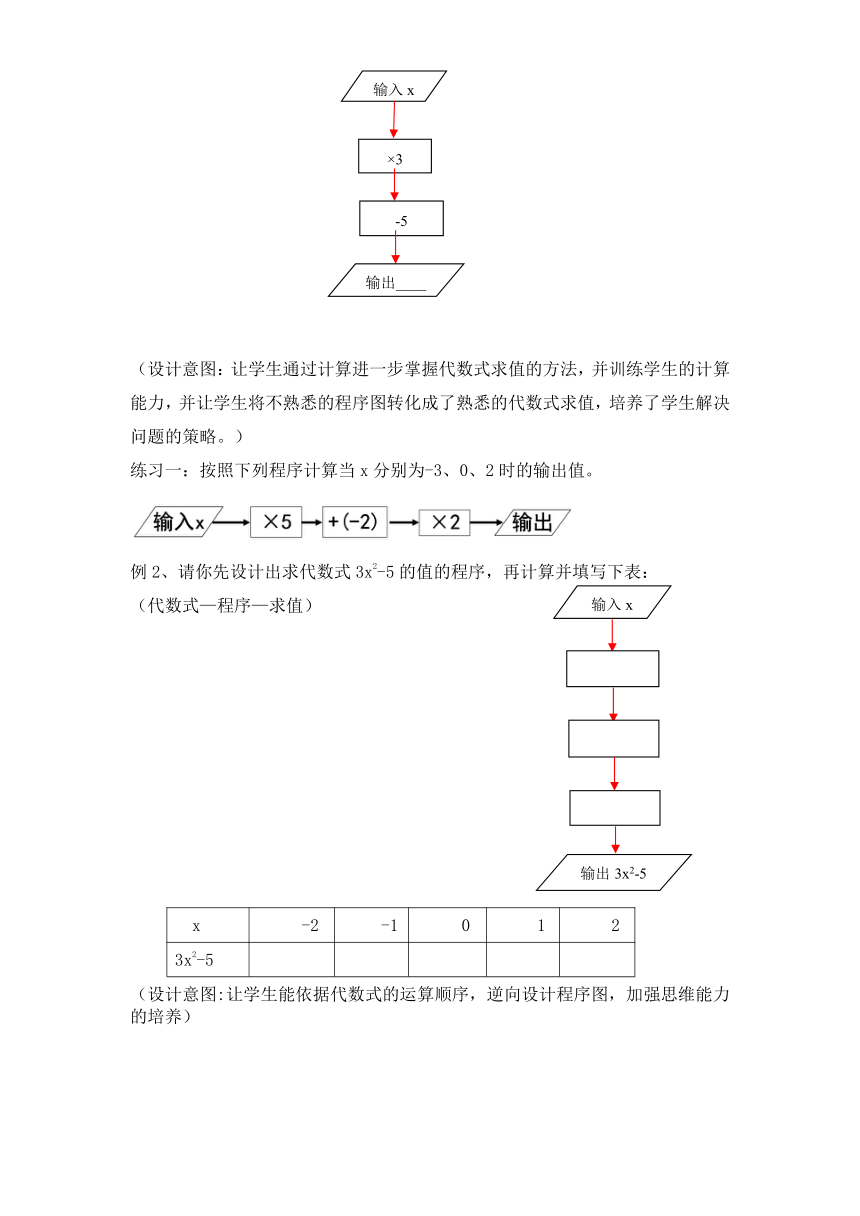
(设计意图:让学生通过计算进一步掌握代数式求值的方法,并训练学生的计算能力,并让学生将不熟悉的程序图转化成了熟悉的代数式求值,培养了学生解决问题的策略。)
练习一:按照下列程序计算当x分别为-3、0、2时的输出值。
例2、请你先设计出求代数式3x2-5的值的程序,再计算并填写下表:
(代数式—程序—求值)
x -2 -1 0 1 2
3x2-5
(设计意图:让学生能依据代数式的运算顺序,逆向设计程序图,加强思维能力的培养)
练习二:请你先在右图中设计出计算代数式2(x-1)2+1的值的计算程序,再计算并填写下表:
x -2 -1 0 1 2
2(x-1)2+1
例3、小明的爸爸存入2年期的教育储蓄9000元(2年期教育储蓄的年利率为4%),到期后本息和(本金与利息的和)自动转存2年期的教育储蓄,像这样至少要储蓄几次才能使本息和超过10 000元.请你用如图所示的程序,帮小明的爸爸算一算.
分析:小明的爸爸存入2年期教育储蓄9000元,到期后的
本息和为多少?如果不满10 000元,再将所得的本息和续存2
年期教育储蓄;到期后的本息和能满10 000元吗?如果不满,
再继续储蓄……直至超过10 000元.
如何简明地表示这样的计算过程呢?(引导学生讨论交
流,继而组织学生阅读课本的计算框图,并向学生介绍判断框
)
(设计意图:由数学到生活,运用已学,理解程序图并正确计算。)
练习三:某工厂生产一种产品,每件成本800元,若平均每年成本下降10%,
试利用图示的计算程序,求出几年后每件产品的成本低于700元?
四、巩固提升
1. 在下列计算程序中填写适当的数或转换步骤:
2.小明编制了一个如图所示的计算程序,当输入2后,最后输出的结果是______。
3.先设计出计算代数式的计算程序,再计算:
(1)若输入x=0,y=-1,则输出为____
(2) 若输入x=2,y=,则输出为______
【课堂小结】
1.如果先给你计算程序,第一步把计算程序要表达的代数式表示出来.第二步实质在做求代数式值的工作.
2.如果给你代数式让你设计计算程序,只要严格按照有理数混合运算的运算顺序再结合设计计算框图的规范要求来设计.
3.通过本节课的学习你收获了哪些?还有什么疑问?
输入x
×3
-5
输出____
输入x
输出3x2-5
输入9000
×(1+4%×2)
>10000
输出
是
否
输入____
+1
( )2
输出25
输入2
输出-15
输入2
( )2
+1
输出______
【教学目标】
知识与能力:1.能读懂计算程序图(框图),会按照规定的程序计算代数式的值。
2.会按照要求设计简单的计算程序,初步感受“算法”的思想。
过程与方法:1.经历探索按程序求值的过程。
2.经历探索已知代数式写出程序的过程,感悟互逆的思维活动。
情感、态度与价值观:通过使学生明白数学来源于生活,学习数学是为了解决实际问题,培养学生科学的学习态度。
【教学重点】 会按规定的程序计算代数式的值,会按要求设计简单的计算程序.
【教学难点】已知代数式,设计程序。
【教学过程】
1、回忆旧知
当x = -1时,求代数式 的值。
(设计意图:回忆代数式的值(1)的内容,再次提醒学生代数式求值的注意点,为新课服务)
2、创设情境
同学们任意说一个整数,把这个数加上5,再乘4,然后减去20,再乘以2,最后除以4,老师可以立马报出答案。你知道其中的奥秘吗?
请学生在心里想一个数,并算出结果,再把心里想的数报给老师,老师可以立马告诉大家输出的数是多少。其中有什么奥秘呢?带着这个疑问,我们来学习今天的内容。 首先我们来学习下图形符号的功能。(多媒体显示):
是输入、输出框,表示最初输入的数值和最终输出的数值;
是处理框(执行框),表示流入此框的数值要进行某种运算,并将
运算结果的数值流出;
是流程线,用来连接程序框,表示数值的流动方向
(设计意图:通过小程序调动学生学习积极性,让学生感受到数学来源生活,引
入本节课知识点并介绍图形符号的功能)
三、例题讲解
例1、按计算程序计算并填写下表:(程序-代数式-求值)
输入 -3 - -1 0 1.5 5
输出
(设计意图:让学生通过计算进一步掌握代数式求值的方法,并训练学生的计算能力,并让学生将不熟悉的程序图转化成了熟悉的代数式求值,培养了学生解决问题的策略。)
练习一:按照下列程序计算当x分别为-3、0、2时的输出值。
例2、请你先设计出求代数式3x2-5的值的程序,再计算并填写下表:
(代数式—程序—求值)
x -2 -1 0 1 2
3x2-5
(设计意图:让学生能依据代数式的运算顺序,逆向设计程序图,加强思维能力的培养)
练习二:请你先在右图中设计出计算代数式2(x-1)2+1的值的计算程序,再计算并填写下表:
x -2 -1 0 1 2
2(x-1)2+1
例3、小明的爸爸存入2年期的教育储蓄9000元(2年期教育储蓄的年利率为4%),到期后本息和(本金与利息的和)自动转存2年期的教育储蓄,像这样至少要储蓄几次才能使本息和超过10 000元.请你用如图所示的程序,帮小明的爸爸算一算.
分析:小明的爸爸存入2年期教育储蓄9000元,到期后的
本息和为多少?如果不满10 000元,再将所得的本息和续存2
年期教育储蓄;到期后的本息和能满10 000元吗?如果不满,
再继续储蓄……直至超过10 000元.
如何简明地表示这样的计算过程呢?(引导学生讨论交
流,继而组织学生阅读课本的计算框图,并向学生介绍判断框
)
(设计意图:由数学到生活,运用已学,理解程序图并正确计算。)
练习三:某工厂生产一种产品,每件成本800元,若平均每年成本下降10%,
试利用图示的计算程序,求出几年后每件产品的成本低于700元?
四、巩固提升
1. 在下列计算程序中填写适当的数或转换步骤:
2.小明编制了一个如图所示的计算程序,当输入2后,最后输出的结果是______。
3.先设计出计算代数式的计算程序,再计算:
(1)若输入x=0,y=-1,则输出为____
(2) 若输入x=2,y=,则输出为______
【课堂小结】
1.如果先给你计算程序,第一步把计算程序要表达的代数式表示出来.第二步实质在做求代数式值的工作.
2.如果给你代数式让你设计计算程序,只要严格按照有理数混合运算的运算顺序再结合设计计算框图的规范要求来设计.
3.通过本节课的学习你收获了哪些?还有什么疑问?
输入x
×3
-5
输出____
输入x
输出3x2-5
输入9000
×(1+4%×2)
>10000
输出
是
否
输入____
+1
( )2
输出25
输入2
输出-15
输入2
( )2
+1
输出______
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
