苏科版七年级上册数学 3.4合并同类项 教案
文档属性
| 名称 | 苏科版七年级上册数学 3.4合并同类项 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 221.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 07:57:40 | ||
图片预览

文档简介
3.4 合并同类项
1.教学目标:了解同类项的概念,能正确判断同类项,掌握合并同类项法则,会合并同类项.
2.教学重点、难点:正确判断同类项,会合并同类项.
3.教学方法与教学手段:启发式探究教学法,多媒体与黑板交互结合的教学手段
4.教学过程:
【创设情境】
红灯笼早餐店
小红:老板,来点早餐!我家三口人,爸爸要4个包子,2个鸡蛋,1杯豆浆;妈妈要2个包子,2个鸡蛋,1杯豆浆;我要2个包子,1个鸡蛋,1杯豆浆.一共多少钱
老板:小朋友,你能不能说清楚点?
(注:每个包子a元,每个鸡蛋b元,每杯豆浆c元)
(按照每人购买的付款总额为4a+2b+c + 2a+2b+c + 2a+b+c,按照购买总数购买的付款总额为8a+5b+3c)
发现:4a+2b+c + 2a+2b+c + 2a+b+c = 8a+5b+3c
【探索新知】
探索一:同类项
回顾:求多项式5a2-8ab+b2+3ab-4a2-b2+5ab的值,其中a=2,b=-1.
思考:除了直接代入、求值,有没有其他简便一些的方法来计算求值呢?
这个多项式中,哪些项具有相同的特征,可以把它们归为一类? .
特征:①
②
定义: ,并且 的项叫做同类项.
注: 都是同类项.
牛刀小试
1.下列各组中的单项式是不是同类项 说明理由.
(1) 7ab和8bc
(2) 2xy和4x3y
(3) x3y2和-3y3x2
(4)-2.5和42
(5) 23和x3
2.已知单项式xmy2与-6x3bn+1是同类项,则m=_______,n=_______.
3.任意说出一个单项式,你能说出这个单项式的同类项吗?你能说出多少个?
注:同类项与 无关,与 无关.
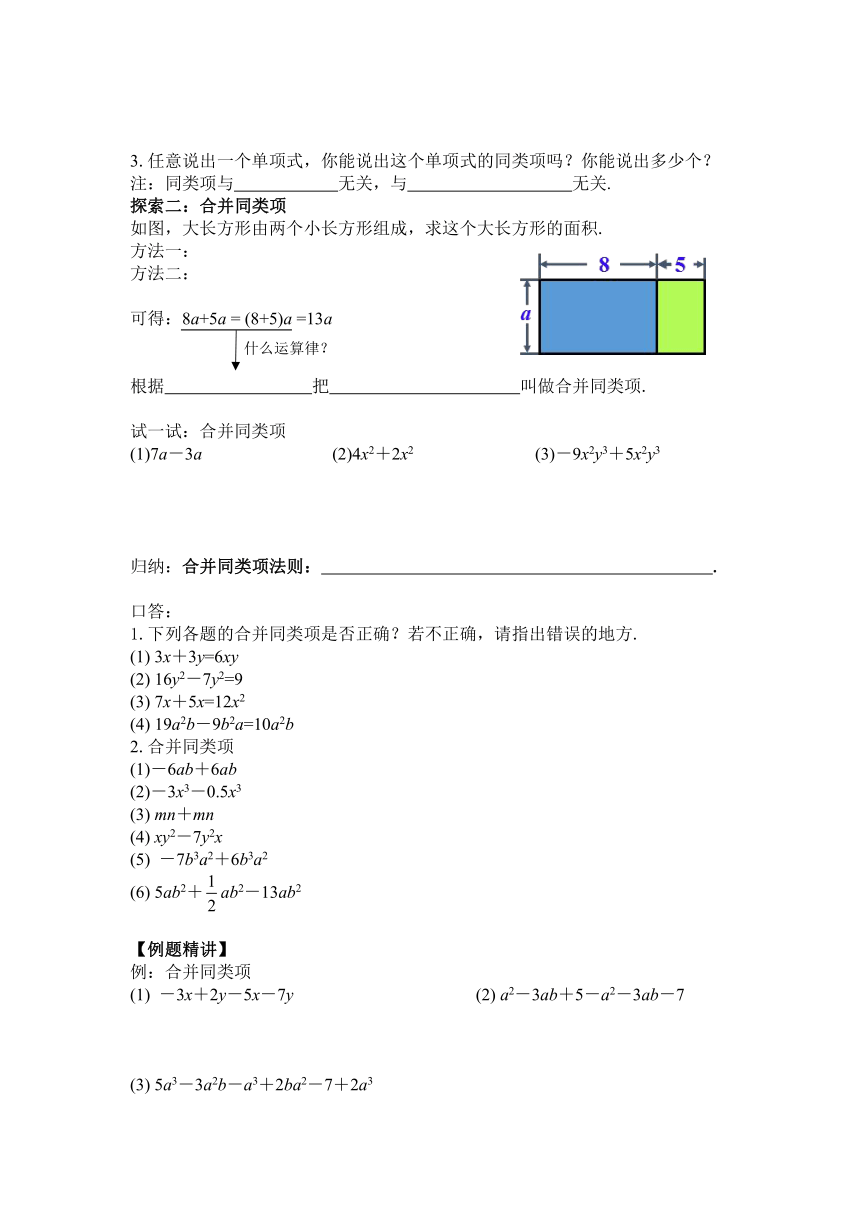
探索二:合并同类项
如图,大长方形由两个小长方形组成,求这个大长方形的面积.
方法一:
方法二:
可得:8a+5a = (8+5)a =13a
根据 把 叫做合并同类项.
试一试:合并同类项
(1)7a-3a (2)4x2+2x2 (3)-9x2y3+5x2y3
归纳:合并同类项法则: .
口答:
1.下列各题的合并同类项是否正确?若不正确,请指出错误的地方.
(1) 3x+3y=6xy
(2) 16y2-7y2=9
(3) 7x+5x=12x2
(4) 19a2b-9b2a=10a2b
2.合并同类项
(1)-6ab+6ab
(2)-3x3-0.5x3
(3) mn+mn
(4) xy2-7y2x
(5) -7b3a2+6b3a2
(6) 5ab2+ab2-13ab2
【例题精讲】
例:合并同类项
(1) -3x+2y-5x-7y (2) a2-3ab+5-a2-3ab-7
(3) 5a3-3a2b-a3+2ba2-7+2a3
练习:
(1) x2-5xy+yx+x2 (2) a2-3a-3a2+a2+2a-7
(3) -4ab+8a-2b2-9ab-8a (4) x2y-3xy2+2yx2-y2x2
【活学活用】
1.已知单项式5a3bm与2am+nb的和仍是单项式,则m=_______,n=_______.
2.多项式2x2-3x2y+mx2y-3x2的值与y的取值无关,则m=_______.
【归纳小结】
通过本节课的学习,你有哪些收获?
教学设计说明
本节课的重点是同类项的概念和合并同类项法则,难点是掌握合并同类项法则,并会合并同类项。
本节课的情境创设,引用了贴近生活的买早餐的例子,通过这个实例列出两个不同的代数式来表示付款总额,引导学生发现这两个代数式是相等关系的,体会到把具有相同特征的事物归为一类后,可使事情的描述变得言简意赅、所列的代数式也能变得更简洁。
接着就引导学生思考,在上一节课《求代数式的值》中,有这样一道题:“求多项式5a2-8ab+b2+3ab-4a2-b2+5ab的值,其中a=2,b=-1.”在代入、求值之前,能不能也把代数式先变得简洁一些,从而使代入、求值更简便?在这个多项式中有哪些项具有相同的特征,可以归为一类?从而引导学生说出他们分类的依据(即同类项的两个特征),引出同类项的概念。通过一道判断改错题、一道填空题、一道开放性题(给出一个单项式,说出它的同类项,能说出多少个),强化学生对同类项概念中两个特征的理解和记忆,并且体会“与系数无关、与字母的顺序无关”。
然后通过由两个小长方形操场组成的大长方形操场的面积的两种表示方法,引导学生发现“8a+5a = (8+5)a =13a”,依据“乘法分配律”可使同类项8a、5a相加后变成一项,从而引出合并同类项的概念。接着让学生模仿,逆用乘法分配律,进行简单的合并同类项,强化学生对“合并同类项的依据——乘法分配律”的理解。然后引导学生概括合并同类项的两个步骤,即合并同类项法则,并通过一组判断改错题和一组简单的合并同类项的口答题,加深对法则的理解和掌握。
例题的教学是在这两组口答题的基础上,加大了难度,从一组同类项,变成两组或三组同类项,其中还有一些项是没有同类项的,不能合并。其中的难点在于学生对几组同类项分别合并后,中间用什么符号连接?在教学时,通过:
1、划线找出同类项;
2、强调多项式是几个单项式的“和”,运用加法交换律把同类项交换位置,使同一组的同类项交换到一起,并且继续划线,便于下一步分组合并时正确找出系数,同时,还要强调交换位置时,每一项都要连同前面的符号一起交换;
3、分组合并时,分别把每组同类项的系数在括号内相加,此时,每组同类项合并的结果之间要用省略的“+”号还原之后来连接;
4、如果合并结果的系数为负数,则用于连接的“+”号要再次省略。
用这4个步骤来分解难点,避免符号理解的困难和错误。然后进行巩固练习,加深理解。
最后的两道拓展提高是对同类项和合并同类项概念的理解的提升,考查了学生对这两个概念的灵活应用的能力。
什么运算律?
合并
同类项
概念
法则
方法
同类项
合并
同类项
寻找、
交换、合并
1.教学目标:了解同类项的概念,能正确判断同类项,掌握合并同类项法则,会合并同类项.
2.教学重点、难点:正确判断同类项,会合并同类项.
3.教学方法与教学手段:启发式探究教学法,多媒体与黑板交互结合的教学手段
4.教学过程:
【创设情境】
红灯笼早餐店
小红:老板,来点早餐!我家三口人,爸爸要4个包子,2个鸡蛋,1杯豆浆;妈妈要2个包子,2个鸡蛋,1杯豆浆;我要2个包子,1个鸡蛋,1杯豆浆.一共多少钱
老板:小朋友,你能不能说清楚点?
(注:每个包子a元,每个鸡蛋b元,每杯豆浆c元)
(按照每人购买的付款总额为4a+2b+c + 2a+2b+c + 2a+b+c,按照购买总数购买的付款总额为8a+5b+3c)
发现:4a+2b+c + 2a+2b+c + 2a+b+c = 8a+5b+3c
【探索新知】
探索一:同类项
回顾:求多项式5a2-8ab+b2+3ab-4a2-b2+5ab的值,其中a=2,b=-1.
思考:除了直接代入、求值,有没有其他简便一些的方法来计算求值呢?
这个多项式中,哪些项具有相同的特征,可以把它们归为一类? .
特征:①
②
定义: ,并且 的项叫做同类项.
注: 都是同类项.
牛刀小试
1.下列各组中的单项式是不是同类项 说明理由.
(1) 7ab和8bc
(2) 2xy和4x3y
(3) x3y2和-3y3x2
(4)-2.5和42
(5) 23和x3
2.已知单项式xmy2与-6x3bn+1是同类项,则m=_______,n=_______.
3.任意说出一个单项式,你能说出这个单项式的同类项吗?你能说出多少个?
注:同类项与 无关,与 无关.
探索二:合并同类项
如图,大长方形由两个小长方形组成,求这个大长方形的面积.
方法一:
方法二:
可得:8a+5a = (8+5)a =13a
根据 把 叫做合并同类项.
试一试:合并同类项
(1)7a-3a (2)4x2+2x2 (3)-9x2y3+5x2y3
归纳:合并同类项法则: .
口答:
1.下列各题的合并同类项是否正确?若不正确,请指出错误的地方.
(1) 3x+3y=6xy
(2) 16y2-7y2=9
(3) 7x+5x=12x2
(4) 19a2b-9b2a=10a2b
2.合并同类项
(1)-6ab+6ab
(2)-3x3-0.5x3
(3) mn+mn
(4) xy2-7y2x
(5) -7b3a2+6b3a2
(6) 5ab2+ab2-13ab2
【例题精讲】
例:合并同类项
(1) -3x+2y-5x-7y (2) a2-3ab+5-a2-3ab-7
(3) 5a3-3a2b-a3+2ba2-7+2a3
练习:
(1) x2-5xy+yx+x2 (2) a2-3a-3a2+a2+2a-7
(3) -4ab+8a-2b2-9ab-8a (4) x2y-3xy2+2yx2-y2x2
【活学活用】
1.已知单项式5a3bm与2am+nb的和仍是单项式,则m=_______,n=_______.
2.多项式2x2-3x2y+mx2y-3x2的值与y的取值无关,则m=_______.
【归纳小结】
通过本节课的学习,你有哪些收获?
教学设计说明
本节课的重点是同类项的概念和合并同类项法则,难点是掌握合并同类项法则,并会合并同类项。
本节课的情境创设,引用了贴近生活的买早餐的例子,通过这个实例列出两个不同的代数式来表示付款总额,引导学生发现这两个代数式是相等关系的,体会到把具有相同特征的事物归为一类后,可使事情的描述变得言简意赅、所列的代数式也能变得更简洁。
接着就引导学生思考,在上一节课《求代数式的值》中,有这样一道题:“求多项式5a2-8ab+b2+3ab-4a2-b2+5ab的值,其中a=2,b=-1.”在代入、求值之前,能不能也把代数式先变得简洁一些,从而使代入、求值更简便?在这个多项式中有哪些项具有相同的特征,可以归为一类?从而引导学生说出他们分类的依据(即同类项的两个特征),引出同类项的概念。通过一道判断改错题、一道填空题、一道开放性题(给出一个单项式,说出它的同类项,能说出多少个),强化学生对同类项概念中两个特征的理解和记忆,并且体会“与系数无关、与字母的顺序无关”。
然后通过由两个小长方形操场组成的大长方形操场的面积的两种表示方法,引导学生发现“8a+5a = (8+5)a =13a”,依据“乘法分配律”可使同类项8a、5a相加后变成一项,从而引出合并同类项的概念。接着让学生模仿,逆用乘法分配律,进行简单的合并同类项,强化学生对“合并同类项的依据——乘法分配律”的理解。然后引导学生概括合并同类项的两个步骤,即合并同类项法则,并通过一组判断改错题和一组简单的合并同类项的口答题,加深对法则的理解和掌握。
例题的教学是在这两组口答题的基础上,加大了难度,从一组同类项,变成两组或三组同类项,其中还有一些项是没有同类项的,不能合并。其中的难点在于学生对几组同类项分别合并后,中间用什么符号连接?在教学时,通过:
1、划线找出同类项;
2、强调多项式是几个单项式的“和”,运用加法交换律把同类项交换位置,使同一组的同类项交换到一起,并且继续划线,便于下一步分组合并时正确找出系数,同时,还要强调交换位置时,每一项都要连同前面的符号一起交换;
3、分组合并时,分别把每组同类项的系数在括号内相加,此时,每组同类项合并的结果之间要用省略的“+”号还原之后来连接;
4、如果合并结果的系数为负数,则用于连接的“+”号要再次省略。
用这4个步骤来分解难点,避免符号理解的困难和错误。然后进行巩固练习,加深理解。
最后的两道拓展提高是对同类项和合并同类项概念的理解的提升,考查了学生对这两个概念的灵活应用的能力。
什么运算律?
合并
同类项
概念
法则
方法
同类项
合并
同类项
寻找、
交换、合并
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
