2022-2023学年人教版八年级数学上册暑假预习 第十一章 学时2 与三角形有关的角 学案(有答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册暑假预习 第十一章 学时2 与三角形有关的角 学案(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 897.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 10:53:08 | ||
图片预览


文档简介
第十一章 三角形
学时2 与三角形有关的角
预习指导:预习教材P11-P16
一、三角形内角和定理
三角形三个内角的和等于180°
思考
根据三角形的内角和定理,可知:任何一个三角形至少有________个锐角,最多有________个锐角,最多有________个钝角,最多有________个直角.
例1证明三角形内角和的常见思路是“拼角”,下列三种辅助线,其中能证明“三角形内角和是180°”的有________(填序号).
①如图①,过点C作DE∥AB;
②如图②,过点C作CE∥AB;
③如图③,过AB上一点D作DE∥BC,DF∥AC.
二、直角三角形的性质与判定
1.概念及表示方法:如图,有一个角为90°的三角形,叫做直角三角形.直角三角形可以用符号“Rt△”表示,直角三角形ABC表示方法:Rt△ABC.
2.性质:直角三角形的两个锐角互余.
思考
如果一个三角形是直角三角形,那么这个三角形有两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗?
答:________________________________________________________________________________。
三、三角形的外角及其性质
1.定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.如图,∠ACD是△ABC的一个外角.
2.性质:三角形的外角等于与它不相邻的两个内角的和.如图,∠ACD=∠A+∠B.
思考
(1)三角形共有________个外角.
(2)①三角形的一个外角等于与它相邻的内角时,该三角形是________三角形;
②三角形的每个外角都大于与它相邻的内角时,该三角形是________三角形;
③三角形的一个外角小于与它相邻的内角时,该三角形是________三角形
例2定理:三角形的外角等于与它不相邻的两个内角的和.下面给出该定理的两种证法.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
.
下列说法正确的是 ( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法2只要测量够一百个三角形进行验证,就能证明该定理
C.证法2用特殊到一般法证明了该定理
D.证法1用严谨的推理证明了该定理
预习反馈
检验一下你的预习成果!
1.在△ABC中,若∠A=60°,∠B=65°,则∠C等于 ( )
A.65° B.55° C.45° D.75°
2.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是 ( )
A.120° B.90° C.60° D.30°
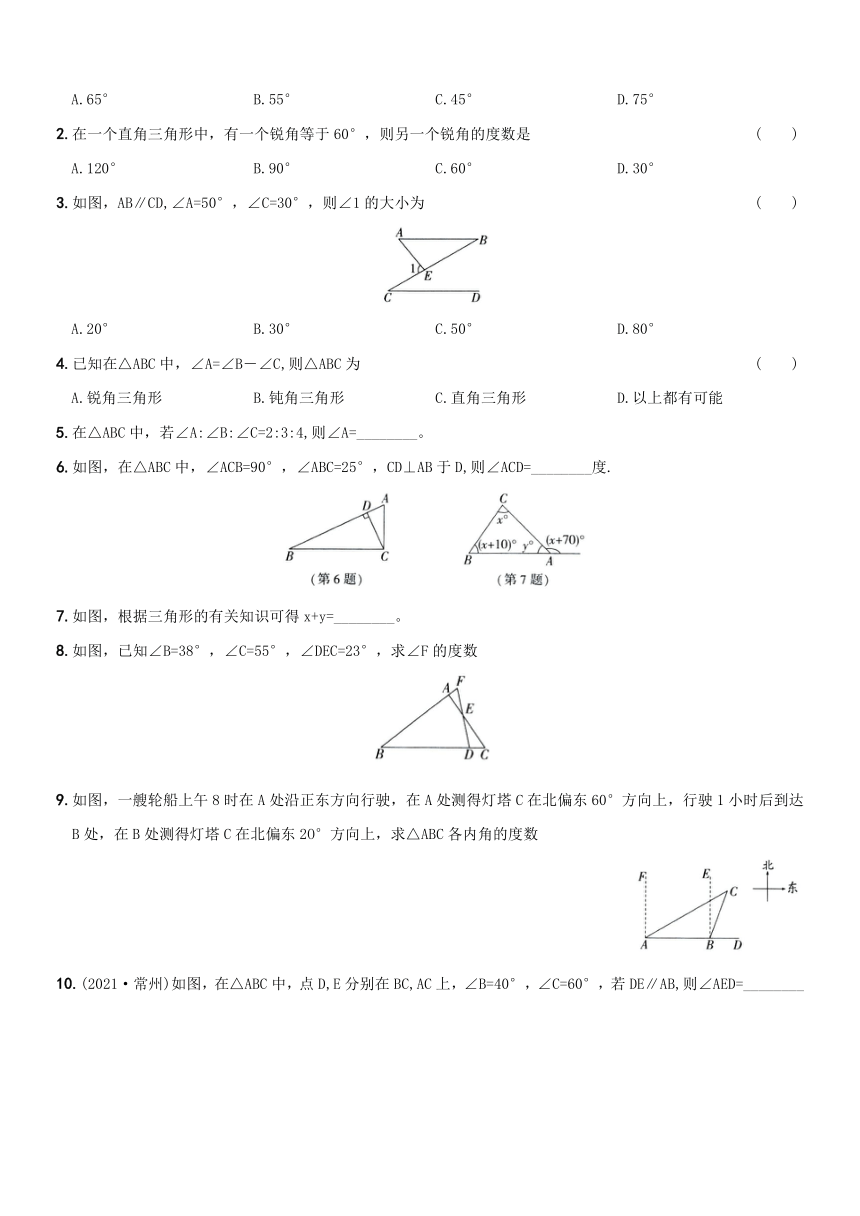
3.如图,AB∥CD,∠A=50°,∠C=30°,则∠1的大小为 ( )
A.20° B.30° C.50° D.80°
4.已知在△ABC中,∠A=∠B-∠C,则△ABC为 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
5.在△ABC中,若∠A:∠B:∠C=2:3:4,则∠A=________。
6.如图,在△ABC中,∠ACB=90°,∠ABC=25°,CD⊥AB于D,则∠ACD=________度.
7.如图,根据三角形的有关知识可得x+y=________。
8.如图,已知∠B=38°,∠C=55°,∠DEC=23°,求∠F的度数
9.如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东2O°方向上,求△ABC各内角的度数
10.(2021·常州)如图,在△ABC中,点D,E分别在BC,AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED=________
11.如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACD的度数为 ( )
A.105° B.110° C.115° D.130°
12.如图,∠BAC=80°,BO,CO分别平分∠ABC和∠ACB,则∠BOC=________
13.(2021·毕节)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为________。
14.如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数
15.如图,AD是△ABC的高,BE平分∠ABC交AD于点E.若∠C=76°,∠BED=64.求∠BAC的度数.
16.如图,在△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D度数.
(2)由第(1)小题的计算,发现∠A和∠D有什么关系?它们是不是一定有这种关系?请说明理由.
【参考答案及解析】
学时2 与三角形有关的角
【预习指导】
一、思考:2 3 1 1
例1 ①②③
二、思考:是
三、思考:(1)6 (2)①直角 ②锐角 ③钝角
例2 D
【预习反馈】
1.B 2.D 3.D 4.C 5.40°
6.25
7.110
8.∵∠B=38°,∠C=55°,∴.∠BAC=180°-38°-55°=87°.
又∵∠DEC=23°,∴∠AEF=23°,∴∠F=∠BAC-∠AEF=87°-23°=64°.
9.∵在A处测得灯塔C在北偏东60°方向上,
∴∠FAC=60°,∴∠CAB=90°-∠FAC=30°.
∵在B处测得灯塔C在北偏东20°方向上,
∴∠EBC=20°,∴∠ABC=90°+∠EBC=110°.
则∠C=180°-∠CAB-∠ABC=180°-30°-110°=40°.
故∠CAB=30°,∠ABC=110°,∠C=40°.
10.100°
11.B
12.130°
解析:∵∠BAC=80°,∴∠ABC+∠ACB=180°-∠BAC=180°-80°=100°.
∵B0,C0分别是∠ABC,∠ACB的平分线,∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×100°=50°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°.
13.75°
解析:如图,
∵∠2=90°-30°=60°,
∴∠3=180°-45°-60°=75°.
∵ab,∴∠1=∠3=75.
14.设∠1=∠2=x,则∠3=∠4=2x.∵∠BAC=63°,∴∠2+∠4=180°-∠BAC=180°-63°=117°,
即x+2x=117°,
∴x=39°,∴∠3=∠4=78°,∠DAC=180°-∠3-∠4=24°.
15.∵AD是△ABC的高,∠C=76°,∴∠DAC=14°.∵BE平分∠ABC交AD于E,
∴∠ABE=∠EBD.∵∠BED=64°,∴.∠ABE+∠BAE=64°,∠EBD+64°=90°,
∴∠EBD=∠ABE=26°,∴∠BAE=38°,∴∠BAC=∠BAE+∠CAD=38°+14°=52°.
16.(1)在△ABC中,∠ABC=60°,∠ACB=40°,∴∠A=180°-∠ABC-∠ACB=80°.
∵BD为∠ABC的平分线,CD为∠ACE的平分线,∴∠DBC=∠ABC=×60°=30°,∵∠DCE=∠ACD=(180°-∠ACB)=×140°=70°.∴∠DCE=∠DBC+∠D,∴∠D=∠DCE-∠DBC=70°-30°=40°,
∴.∠A=80°,∠D=40°.
(2)通过(1)的计算,得到∠A=2∠D.它们一定有这种关系.
理由:∵∠ACE=∠A+∠ABC,∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC.
又BD平分∠ABC,CD平分∠ACE,∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE-∠DBC),∠D=∠DCE-∠DBC,∴∠A=2∠D.
学时2 与三角形有关的角
预习指导:预习教材P11-P16
一、三角形内角和定理
三角形三个内角的和等于180°
思考
根据三角形的内角和定理,可知:任何一个三角形至少有________个锐角,最多有________个锐角,最多有________个钝角,最多有________个直角.
例1证明三角形内角和的常见思路是“拼角”,下列三种辅助线,其中能证明“三角形内角和是180°”的有________(填序号).
①如图①,过点C作DE∥AB;
②如图②,过点C作CE∥AB;
③如图③,过AB上一点D作DE∥BC,DF∥AC.
二、直角三角形的性质与判定
1.概念及表示方法:如图,有一个角为90°的三角形,叫做直角三角形.直角三角形可以用符号“Rt△”表示,直角三角形ABC表示方法:Rt△ABC.
2.性质:直角三角形的两个锐角互余.
思考
如果一个三角形是直角三角形,那么这个三角形有两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗?
答:________________________________________________________________________________。
三、三角形的外角及其性质
1.定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.如图,∠ACD是△ABC的一个外角.
2.性质:三角形的外角等于与它不相邻的两个内角的和.如图,∠ACD=∠A+∠B.
思考
(1)三角形共有________个外角.
(2)①三角形的一个外角等于与它相邻的内角时,该三角形是________三角形;
②三角形的每个外角都大于与它相邻的内角时,该三角形是________三角形;
③三角形的一个外角小于与它相邻的内角时,该三角形是________三角形
例2定理:三角形的外角等于与它不相邻的两个内角的和.下面给出该定理的两种证法.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
.
下列说法正确的是 ( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法2只要测量够一百个三角形进行验证,就能证明该定理
C.证法2用特殊到一般法证明了该定理
D.证法1用严谨的推理证明了该定理
预习反馈
检验一下你的预习成果!
1.在△ABC中,若∠A=60°,∠B=65°,则∠C等于 ( )
A.65° B.55° C.45° D.75°
2.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是 ( )
A.120° B.90° C.60° D.30°
3.如图,AB∥CD,∠A=50°,∠C=30°,则∠1的大小为 ( )
A.20° B.30° C.50° D.80°
4.已知在△ABC中,∠A=∠B-∠C,则△ABC为 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
5.在△ABC中,若∠A:∠B:∠C=2:3:4,则∠A=________。
6.如图,在△ABC中,∠ACB=90°,∠ABC=25°,CD⊥AB于D,则∠ACD=________度.
7.如图,根据三角形的有关知识可得x+y=________。
8.如图,已知∠B=38°,∠C=55°,∠DEC=23°,求∠F的度数
9.如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东2O°方向上,求△ABC各内角的度数
10.(2021·常州)如图,在△ABC中,点D,E分别在BC,AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED=________
11.如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACD的度数为 ( )
A.105° B.110° C.115° D.130°
12.如图,∠BAC=80°,BO,CO分别平分∠ABC和∠ACB,则∠BOC=________
13.(2021·毕节)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为________。
14.如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数
15.如图,AD是△ABC的高,BE平分∠ABC交AD于点E.若∠C=76°,∠BED=64.求∠BAC的度数.
16.如图,在△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D度数.
(2)由第(1)小题的计算,发现∠A和∠D有什么关系?它们是不是一定有这种关系?请说明理由.
【参考答案及解析】
学时2 与三角形有关的角
【预习指导】
一、思考:2 3 1 1
例1 ①②③
二、思考:是
三、思考:(1)6 (2)①直角 ②锐角 ③钝角
例2 D
【预习反馈】
1.B 2.D 3.D 4.C 5.40°
6.25
7.110
8.∵∠B=38°,∠C=55°,∴.∠BAC=180°-38°-55°=87°.
又∵∠DEC=23°,∴∠AEF=23°,∴∠F=∠BAC-∠AEF=87°-23°=64°.
9.∵在A处测得灯塔C在北偏东60°方向上,
∴∠FAC=60°,∴∠CAB=90°-∠FAC=30°.
∵在B处测得灯塔C在北偏东20°方向上,
∴∠EBC=20°,∴∠ABC=90°+∠EBC=110°.
则∠C=180°-∠CAB-∠ABC=180°-30°-110°=40°.
故∠CAB=30°,∠ABC=110°,∠C=40°.
10.100°
11.B
12.130°
解析:∵∠BAC=80°,∴∠ABC+∠ACB=180°-∠BAC=180°-80°=100°.
∵B0,C0分别是∠ABC,∠ACB的平分线,∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×100°=50°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°.
13.75°
解析:如图,
∵∠2=90°-30°=60°,
∴∠3=180°-45°-60°=75°.
∵ab,∴∠1=∠3=75.
14.设∠1=∠2=x,则∠3=∠4=2x.∵∠BAC=63°,∴∠2+∠4=180°-∠BAC=180°-63°=117°,
即x+2x=117°,
∴x=39°,∴∠3=∠4=78°,∠DAC=180°-∠3-∠4=24°.
15.∵AD是△ABC的高,∠C=76°,∴∠DAC=14°.∵BE平分∠ABC交AD于E,
∴∠ABE=∠EBD.∵∠BED=64°,∴.∠ABE+∠BAE=64°,∠EBD+64°=90°,
∴∠EBD=∠ABE=26°,∴∠BAE=38°,∴∠BAC=∠BAE+∠CAD=38°+14°=52°.
16.(1)在△ABC中,∠ABC=60°,∠ACB=40°,∴∠A=180°-∠ABC-∠ACB=80°.
∵BD为∠ABC的平分线,CD为∠ACE的平分线,∴∠DBC=∠ABC=×60°=30°,∵∠DCE=∠ACD=(180°-∠ACB)=×140°=70°.∴∠DCE=∠DBC+∠D,∴∠D=∠DCE-∠DBC=70°-30°=40°,
∴.∠A=80°,∠D=40°.
(2)通过(1)的计算,得到∠A=2∠D.它们一定有这种关系.
理由:∵∠ACE=∠A+∠ABC,∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC.
又BD平分∠ABC,CD平分∠ACE,∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE-∠DBC),∠D=∠DCE-∠DBC,∴∠A=2∠D.
