2022-2023学年人教版八年级数学上册暑假预习 第十一章 学时3 多边形及其肉角和 学案(有答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册暑假预习 第十一章 学时3 多边形及其肉角和 学案(有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 765.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 10:53:37 | ||
图片预览

文档简介
第十一章 三角形
学时3 多边形及其内角和
预习指导:预习教材P19-P24
一、多边形及其有关概念
1.定义:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
2.边:组成多边形的线段叫做多边形的边.
3.内角:多边形相邻两边组成的角叫做多边形的内角,也称为多边形的角;
4.外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
5.对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
6.正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
7.凸多边形:画出多边形的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的多边形称为凸多边形.
思考
(1)多边形的对角线是一条________(填“线段”“射线”或“直线”)
(2)从n边形的每个顶点可画________条对角线,但由于每个顶点所画的对角线都重复一次,则n边形共有________条对角线;
(3)每个顶点的对角线把这个n边形共分成了________个三角形
二、多边形的内角和与外角和
1.多边形的内角和公式:n边形内角和等于(n-2)×180°.
2.多边形的外角和定理:多边形的外角和等于360°
思考
(1)多边形的外角和与边数n________.(填“有关”或“无关”)
(2)多边形内角和公式的证明基本上都是先将多边形的内角进行分割,然后把它们放在三角形中进行证明,依据是________________________________。
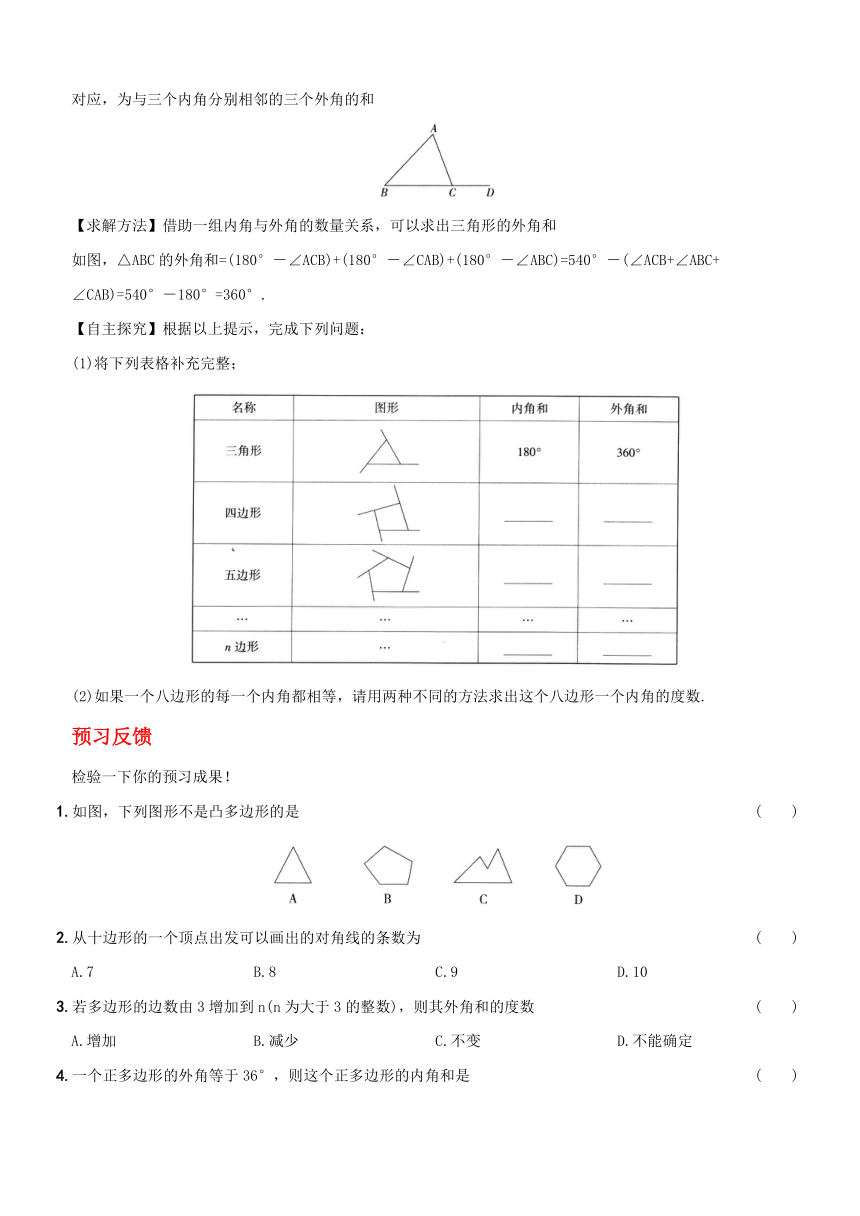
例【相关概念】将多边形的内角一边反向延长,与另一条边相夹形成的那个角叫做多边形的外角.如图,将△ABC中∠ACB的边CB反向延长,与另一边AC形成的∠ACD即为△ACB的一个外角.三角形外角和与三角形内角和对应,为与三个内角分别相邻的三个外角的和
【求解方法】借助一组内角与外角的数量关系,可以求出三角形的外角和
如图,△ABC的外角和=(180°-∠ACB)+(180°-∠CAB)+(180°-∠ABC)=540°-(∠ACB+∠ABC+
∠CAB)=540°-180°=360°.
【自主探究】根据以上提示,完成下列问题:
(1)将下列表格补充完整;
(2)如果一个八边形的每一个内角都相等,请用两种不同的方法求出这个八边形一个内角的度数.
预习反馈
检验一下你的预习成果!
1.如图,下列图形不是凸多边形的是 ( )
2.从十边形的一个顶点出发可以画出的对角线的条数为 ( )
A.7 B.8 C.9 D.10
3.若多边形的边数由3增加到n(n为大于3的整数),则其外角和的度数 ( )
A.增加 B.减少 C.不变 D.不能确定
4.一个正多边形的外角等于36°,则这个正多边形的内角和是 ( )
A.1440° B.1080° C.900° D.720°
5.已知一个多边形的每一个内角都相等,且每一个内角与一个外角的度数比为5∶1,则这个多边形的边数是________。
6.如图,在四边形ABCD中,∠A=∠D,∠B=∠C,试判断AD与BC的位置关系,并说明理由.
7.下面的多边形中,内角和等于外角和的图形是 ( )
A.三角形 B.四边形 C.五边形 D.六边形
8.如图,在五边形ABCDE中,AB∥CD,∠1+∠2+∠3等于 ( )
A.90° B.180° C.210° D.270°
9.一个凸边形,除去一个内角外其余的内角和是2570°,则这个多边形对角线的条数为________。
1O.如图所示,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,
求证:△DCF为直角三角形.
11.如图①,称△AOB和△COD为“对顶三角形”,其中∠A+∠B=∠C+∠D,利用这个结论,完成下列填空:
(1)如图②,∠A+∠B+∠C+∠D+∠E=________;
(2)如图③,∠A+∠B+∠C+∠D+∠E=________;
(3)如图④,∠1+∠2+∠3+∠4+∠5+∠6=________;
(4)如图⑤,∠1+∠2+∠3+∠4+∠5+∠6+∠7=________
【参考答案及解析】
学时3 多边形及其内角和
【预习指导】
一、思考:(1)线段 (2)(n-3)
(3)(n-2)
二、思考:(1)无关 (2)三角形的内角和是180°
例 (1)360° 360° 540° 360° 180°(n-2) 360°
(2)方法一:(8-2)×180°÷8=135° 方法二:180°-360°÷8=135°
【预习反馈】
1.C 2.A 3.C 4.A 5.12
6.AD与BC的位置关系是平行.理由:∵四边形ABCD的内角和是360°,∴∠A+∠B+∠C+∠D=360°.∵∠A=∠D,∠B=∠C,∴∠A+∠B+∠B+∠A=360°,∴∠A+∠B=180°,∴AD/BC(同旁内角互补,两直线平行).
7.B
解析:任意多边形的外角和等于360°.A.三角形的内角和等于180°,故三角形的内角和与外角和不相等,A不符合题意.B.四边形的内角和等于360°,故四边形的内角和与外角和相等,B符合题意.C.五边形的内角和等于540°,故五边形的内角和与外角和不相.等,C不符合题意.D.六边形的内角和等于720°,故六边形的内角和与外角和不相等,D不符合题意.故选B.
8.B
解析:如图,∵AB∥CD,∴∠4+∠5=180°.∵∠1+∠2+∠3+∠4+∠5=360°,∴∠1+∠2+∠3=360°-180°=180°.
9.119
解析:设这个内角度数为x,边数为n,则(n-2)×180°-x=2570°.180°·n=2930°+x.
∵n为正整数,∴n=17,∴这个多边形的对角线的条数是×17×(17-3)=119.
10.证法一:∵在四边形ABCD中,∠A与∠C互补,∴∠ABC+∠ADC=360°-180°=180°.∵BE平分∠ABC,DF平分∠ADC,∴∠CDF+∠CBE=90O°.∵BE∥DF,∴∠CBE=∠CFD,∴∠CDF+∠CFD=90°,故△DCF为直角三角形.
证法二:在四边形ABCD中,BE平分∠ABC,DF平分∠ADC,∴∠ABE=∠CBE,∠CDF=∠ADF.BE∥DF,∴∠CFD=∠CBE,∠AEB=∠ADF
∴∠CFD=∠ABE,∠CDF=∠AEB,∴∠CFD+∠CDF=∠ABE+∠AEB,∴∠A=∠C.∠A与∠C互补,
∴∠A=∠C=90°,故△DCF为直角三角形.
11.(1)180° (2)180° (3)360° (4)540°
解析:(1)如图①,∵∠1,∠2的和与∠D,∠E的和相等,∴∠BAE+∠B+∠BCD+∠D+∠E=∠BAE+∠B+∠BCD+∠1+∠2=180°.
(2)如图②,∵∠1,∠2的和与∠D,∠E的和相等,∴∠A+∠ABE+∠ACD+∠D+∠E=∠A+∠ABE+∠ACD+∠1+∠2=180°.
(3)如图③,∵∠1,∠2的和与∠7,∠8的和相等,∴∠1+∠2+∠3+∠4+∠5+∠6=∠7+∠8+∠3+∠4+∠5+∠6=360°.
(4)如图④,∵∠6,∠7的和与∠8,∠9的和相等,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=(5-2)×180°=540°
学时3 多边形及其内角和
预习指导:预习教材P19-P24
一、多边形及其有关概念
1.定义:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
2.边:组成多边形的线段叫做多边形的边.
3.内角:多边形相邻两边组成的角叫做多边形的内角,也称为多边形的角;
4.外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
5.对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
6.正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
7.凸多边形:画出多边形的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的多边形称为凸多边形.
思考
(1)多边形的对角线是一条________(填“线段”“射线”或“直线”)
(2)从n边形的每个顶点可画________条对角线,但由于每个顶点所画的对角线都重复一次,则n边形共有________条对角线;
(3)每个顶点的对角线把这个n边形共分成了________个三角形
二、多边形的内角和与外角和
1.多边形的内角和公式:n边形内角和等于(n-2)×180°.
2.多边形的外角和定理:多边形的外角和等于360°
思考
(1)多边形的外角和与边数n________.(填“有关”或“无关”)
(2)多边形内角和公式的证明基本上都是先将多边形的内角进行分割,然后把它们放在三角形中进行证明,依据是________________________________。
例【相关概念】将多边形的内角一边反向延长,与另一条边相夹形成的那个角叫做多边形的外角.如图,将△ABC中∠ACB的边CB反向延长,与另一边AC形成的∠ACD即为△ACB的一个外角.三角形外角和与三角形内角和对应,为与三个内角分别相邻的三个外角的和
【求解方法】借助一组内角与外角的数量关系,可以求出三角形的外角和
如图,△ABC的外角和=(180°-∠ACB)+(180°-∠CAB)+(180°-∠ABC)=540°-(∠ACB+∠ABC+
∠CAB)=540°-180°=360°.
【自主探究】根据以上提示,完成下列问题:
(1)将下列表格补充完整;
(2)如果一个八边形的每一个内角都相等,请用两种不同的方法求出这个八边形一个内角的度数.
预习反馈
检验一下你的预习成果!
1.如图,下列图形不是凸多边形的是 ( )
2.从十边形的一个顶点出发可以画出的对角线的条数为 ( )
A.7 B.8 C.9 D.10
3.若多边形的边数由3增加到n(n为大于3的整数),则其外角和的度数 ( )
A.增加 B.减少 C.不变 D.不能确定
4.一个正多边形的外角等于36°,则这个正多边形的内角和是 ( )
A.1440° B.1080° C.900° D.720°
5.已知一个多边形的每一个内角都相等,且每一个内角与一个外角的度数比为5∶1,则这个多边形的边数是________。
6.如图,在四边形ABCD中,∠A=∠D,∠B=∠C,试判断AD与BC的位置关系,并说明理由.
7.下面的多边形中,内角和等于外角和的图形是 ( )
A.三角形 B.四边形 C.五边形 D.六边形
8.如图,在五边形ABCDE中,AB∥CD,∠1+∠2+∠3等于 ( )
A.90° B.180° C.210° D.270°
9.一个凸边形,除去一个内角外其余的内角和是2570°,则这个多边形对角线的条数为________。
1O.如图所示,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,
求证:△DCF为直角三角形.
11.如图①,称△AOB和△COD为“对顶三角形”,其中∠A+∠B=∠C+∠D,利用这个结论,完成下列填空:
(1)如图②,∠A+∠B+∠C+∠D+∠E=________;
(2)如图③,∠A+∠B+∠C+∠D+∠E=________;
(3)如图④,∠1+∠2+∠3+∠4+∠5+∠6=________;
(4)如图⑤,∠1+∠2+∠3+∠4+∠5+∠6+∠7=________
【参考答案及解析】
学时3 多边形及其内角和
【预习指导】
一、思考:(1)线段 (2)(n-3)
(3)(n-2)
二、思考:(1)无关 (2)三角形的内角和是180°
例 (1)360° 360° 540° 360° 180°(n-2) 360°
(2)方法一:(8-2)×180°÷8=135° 方法二:180°-360°÷8=135°
【预习反馈】
1.C 2.A 3.C 4.A 5.12
6.AD与BC的位置关系是平行.理由:∵四边形ABCD的内角和是360°,∴∠A+∠B+∠C+∠D=360°.∵∠A=∠D,∠B=∠C,∴∠A+∠B+∠B+∠A=360°,∴∠A+∠B=180°,∴AD/BC(同旁内角互补,两直线平行).
7.B
解析:任意多边形的外角和等于360°.A.三角形的内角和等于180°,故三角形的内角和与外角和不相等,A不符合题意.B.四边形的内角和等于360°,故四边形的内角和与外角和相等,B符合题意.C.五边形的内角和等于540°,故五边形的内角和与外角和不相.等,C不符合题意.D.六边形的内角和等于720°,故六边形的内角和与外角和不相等,D不符合题意.故选B.
8.B
解析:如图,∵AB∥CD,∴∠4+∠5=180°.∵∠1+∠2+∠3+∠4+∠5=360°,∴∠1+∠2+∠3=360°-180°=180°.
9.119
解析:设这个内角度数为x,边数为n,则(n-2)×180°-x=2570°.180°·n=2930°+x.
∵n为正整数,∴n=17,∴这个多边形的对角线的条数是×17×(17-3)=119.
10.证法一:∵在四边形ABCD中,∠A与∠C互补,∴∠ABC+∠ADC=360°-180°=180°.∵BE平分∠ABC,DF平分∠ADC,∴∠CDF+∠CBE=90O°.∵BE∥DF,∴∠CBE=∠CFD,∴∠CDF+∠CFD=90°,故△DCF为直角三角形.
证法二:在四边形ABCD中,BE平分∠ABC,DF平分∠ADC,∴∠ABE=∠CBE,∠CDF=∠ADF.BE∥DF,∴∠CFD=∠CBE,∠AEB=∠ADF
∴∠CFD=∠ABE,∠CDF=∠AEB,∴∠CFD+∠CDF=∠ABE+∠AEB,∴∠A=∠C.∠A与∠C互补,
∴∠A=∠C=90°,故△DCF为直角三角形.
11.(1)180° (2)180° (3)360° (4)540°
解析:(1)如图①,∵∠1,∠2的和与∠D,∠E的和相等,∴∠BAE+∠B+∠BCD+∠D+∠E=∠BAE+∠B+∠BCD+∠1+∠2=180°.
(2)如图②,∵∠1,∠2的和与∠D,∠E的和相等,∴∠A+∠ABE+∠ACD+∠D+∠E=∠A+∠ABE+∠ACD+∠1+∠2=180°.
(3)如图③,∵∠1,∠2的和与∠7,∠8的和相等,∴∠1+∠2+∠3+∠4+∠5+∠6=∠7+∠8+∠3+∠4+∠5+∠6=360°.
(4)如图④,∵∠6,∠7的和与∠8,∠9的和相等,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=(5-2)×180°=540°
