2022-2023学年人教版八年级数学上册暑假预习 第十一章 三角形(章节综合自测) 学案(有答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册暑假预习 第十一章 三角形(章节综合自测) 学案(有答案) | 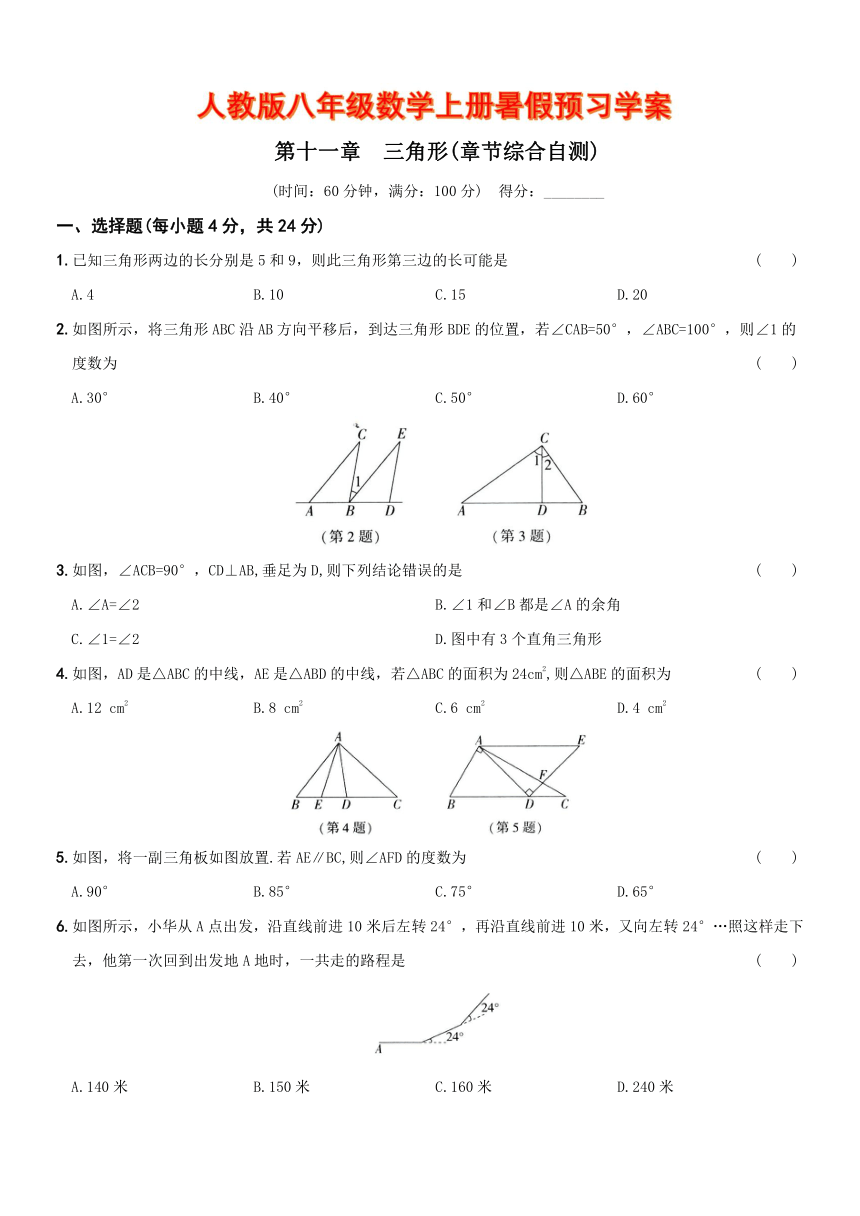 | |
| 格式 | docx | ||
| 文件大小 | 403.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 10:57:45 | ||
图片预览


文档简介
第十一章 三角形(章节综合自测)
(时间:60分钟,满分:100分) 得分:________
一、选择题(每小题4分,共24分)
1.已知三角形两边的长分别是5和9,则此三角形第三边的长可能是 ( )
A.4 B.10 C.15 D.20
2.如图所示,将三角形ABC沿AB方向平移后,到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠1的度数为 ( )
A.30° B.40° C.50° D.60°
3.如图,∠ACB=90°,CD⊥AB,垂足为D,则下列结论错误的是 ( )
A.∠A=∠2 B.∠1和∠B都是∠A的余角
C.∠1=∠2 D.图中有3个直角三角形
4.如图,AD是△ABC的中线,AE是△ABD的中线,若△ABC的面积为24cm2,则△ABE的面积为 ( )
A.12 cm2 B.8 cm2 C.6 cm2 D.4 cm2
5.如图,将一副三角板如图放置.若AE∥BC,则∠AFD的度数为 ( )
A.90° B.85° C.75° D.65°
6.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°…照这样走下去,他第一次回到出发地A地时,一共走的路程是 ( )
A.140米 B.150米 C.160米 D.240米
二、填空题(每小题5分,共30分)
7.一棵小树被风刮歪了,小明用三根木棒撑住这棵小树,他运用的数学知识是三角形具有________。
8.内角和与外角和相等的多边形的边数为________。
9.如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°.现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为________
10.若一个多边形截去一个角后,变成六边形,则原来多边形的边数可能是________。
11.一个三角形3条边长分别为xcm、(x+1)cm、(x+2)cm,它的周长不超过39cm,则x的取值范围是________
12.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P=________。
三、解答题(共46分)
13.(10分)已知a,b,c是△ABC的三边,a=4,b=6,若三角形的周长是小于18的偶数
(1)求c的长;
(2)判断△ABC的形状.
14.(10分)如图,∠B=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.
15.(12分)如图,在△ABC中,AD平分∠BAC,P为线段AD.上的一个动点,PE⊥AD交直线BC于点E,若∠B=35°,∠ACB=85°.
(1)求∠DAC的度数;
(2)求∠E的度数.
16.(14分)在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的平分线交于点E,试求出∠BEC的度数.
【参考答案及解析】
第十一章 自测卷
1.B 2.A 3.C 4.C
5.C
解析:结合三角板考查三角形外角性质,∠AFD=∠E+∠CAE=∠C+∠E=30°+45°=75°.
6.B
解析:多边形的外角和为360°,而每一个外角为24°,∴多边形的边数为360°÷24°=15,∴小华一共走的路程是15×10=150(米),故选B.
7.稳定性
8.4
9.80°
10.5,6,7
11.1解析:由题意得,解得112.90°
解析:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∠ABP=20°,∠ACP=50°,∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,∴∠A=∠ACM-∠ABC=60°,∠ACB=180°-∠ACM=80°.∴∠BCP=∠ACB+∠ACP=130°.∠PBC=20°,∴∠P=180°-∠PBC-∠BCP=30°,∴∠A+∠P=90°.
13.(1)∵a,b,c是△ABC的三边,a=4,b=6,∴2(2)当c=4或6时,△ABC都是等腰三角形.
14.∵∠B=38°,∠ACB=100°,∴∠BAC=180°-38°-100°=42°.又AD平分∠BAC,∴∠BAD=21°,∴∠ADE=∠B+∠BAD=38°+21°=59°.又AE是BC边上的高,即∠E=90°,∴∠DAE=180°-∠E-∠ADE=180°-90°-59°=31°.
15.(1)∵∠B=35°,∠ACB=85°,∴∠BAC=60°.∵AD平分∠BAC,∴∠DAC=∠BAC=30°.
(2)∵∠BAD=∠BAC=30°,∴∠ADC=35°+30°=65°.∵∠EPD=90°,∴∠E的度数为90°-65°=25°.
16.(1)∵∠A+∠B+∠C+∠D=360°,∠B=∠C,
∴∠B=∠C===70°.
(2)∵BE∥AD,∴∠BEC=∠D=80°,∠ABE=180°-∠A=180°-140°=40°.又BE平分∠ABC,∴∠EBC=∠ABE=40°,∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
(3)∵∠A+∠ABC+∠BCD+∠D=360°,∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°.∵∠ABC和∠BCD的平分线交于点E,∴∠EBC=∠ABC,∠BCE=∠BCD,∴∠E=180°-∠EBC-∠BCE=180°-(∠ABC+∠BCD)=180°-×140°=110°.
(时间:60分钟,满分:100分) 得分:________
一、选择题(每小题4分,共24分)
1.已知三角形两边的长分别是5和9,则此三角形第三边的长可能是 ( )
A.4 B.10 C.15 D.20
2.如图所示,将三角形ABC沿AB方向平移后,到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠1的度数为 ( )
A.30° B.40° C.50° D.60°
3.如图,∠ACB=90°,CD⊥AB,垂足为D,则下列结论错误的是 ( )
A.∠A=∠2 B.∠1和∠B都是∠A的余角
C.∠1=∠2 D.图中有3个直角三角形
4.如图,AD是△ABC的中线,AE是△ABD的中线,若△ABC的面积为24cm2,则△ABE的面积为 ( )
A.12 cm2 B.8 cm2 C.6 cm2 D.4 cm2
5.如图,将一副三角板如图放置.若AE∥BC,则∠AFD的度数为 ( )
A.90° B.85° C.75° D.65°
6.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°…照这样走下去,他第一次回到出发地A地时,一共走的路程是 ( )
A.140米 B.150米 C.160米 D.240米
二、填空题(每小题5分,共30分)
7.一棵小树被风刮歪了,小明用三根木棒撑住这棵小树,他运用的数学知识是三角形具有________。
8.内角和与外角和相等的多边形的边数为________。
9.如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°.现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为________
10.若一个多边形截去一个角后,变成六边形,则原来多边形的边数可能是________。
11.一个三角形3条边长分别为xcm、(x+1)cm、(x+2)cm,它的周长不超过39cm,则x的取值范围是________
12.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P=________。
三、解答题(共46分)
13.(10分)已知a,b,c是△ABC的三边,a=4,b=6,若三角形的周长是小于18的偶数
(1)求c的长;
(2)判断△ABC的形状.
14.(10分)如图,∠B=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.
15.(12分)如图,在△ABC中,AD平分∠BAC,P为线段AD.上的一个动点,PE⊥AD交直线BC于点E,若∠B=35°,∠ACB=85°.
(1)求∠DAC的度数;
(2)求∠E的度数.
16.(14分)在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的平分线交于点E,试求出∠BEC的度数.
【参考答案及解析】
第十一章 自测卷
1.B 2.A 3.C 4.C
5.C
解析:结合三角板考查三角形外角性质,∠AFD=∠E+∠CAE=∠C+∠E=30°+45°=75°.
6.B
解析:多边形的外角和为360°,而每一个外角为24°,∴多边形的边数为360°÷24°=15,∴小华一共走的路程是15×10=150(米),故选B.
7.稳定性
8.4
9.80°
10.5,6,7
11.1
解析:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∠ABP=20°,∠ACP=50°,∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,∴∠A=∠ACM-∠ABC=60°,∠ACB=180°-∠ACM=80°.∴∠BCP=∠ACB+∠ACP=130°.∠PBC=20°,∴∠P=180°-∠PBC-∠BCP=30°,∴∠A+∠P=90°.
13.(1)∵a,b,c是△ABC的三边,a=4,b=6,∴2
14.∵∠B=38°,∠ACB=100°,∴∠BAC=180°-38°-100°=42°.又AD平分∠BAC,∴∠BAD=21°,∴∠ADE=∠B+∠BAD=38°+21°=59°.又AE是BC边上的高,即∠E=90°,∴∠DAE=180°-∠E-∠ADE=180°-90°-59°=31°.
15.(1)∵∠B=35°,∠ACB=85°,∴∠BAC=60°.∵AD平分∠BAC,∴∠DAC=∠BAC=30°.
(2)∵∠BAD=∠BAC=30°,∴∠ADC=35°+30°=65°.∵∠EPD=90°,∴∠E的度数为90°-65°=25°.
16.(1)∵∠A+∠B+∠C+∠D=360°,∠B=∠C,
∴∠B=∠C===70°.
(2)∵BE∥AD,∴∠BEC=∠D=80°,∠ABE=180°-∠A=180°-140°=40°.又BE平分∠ABC,∴∠EBC=∠ABE=40°,∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
(3)∵∠A+∠ABC+∠BCD+∠D=360°,∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°.∵∠ABC和∠BCD的平分线交于点E,∴∠EBC=∠ABC,∠BCE=∠BCD,∴∠E=180°-∠EBC-∠BCE=180°-(∠ABC+∠BCD)=180°-×140°=110°.
