2022-2023学年人教版八年级数学上册暑假预习 第十二章 学时6 利用“ASA”“AAS”判定三角形全等 学案(有答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册暑假预习 第十二章 学时6 利用“ASA”“AAS”判定三角形全等 学案(有答案) | 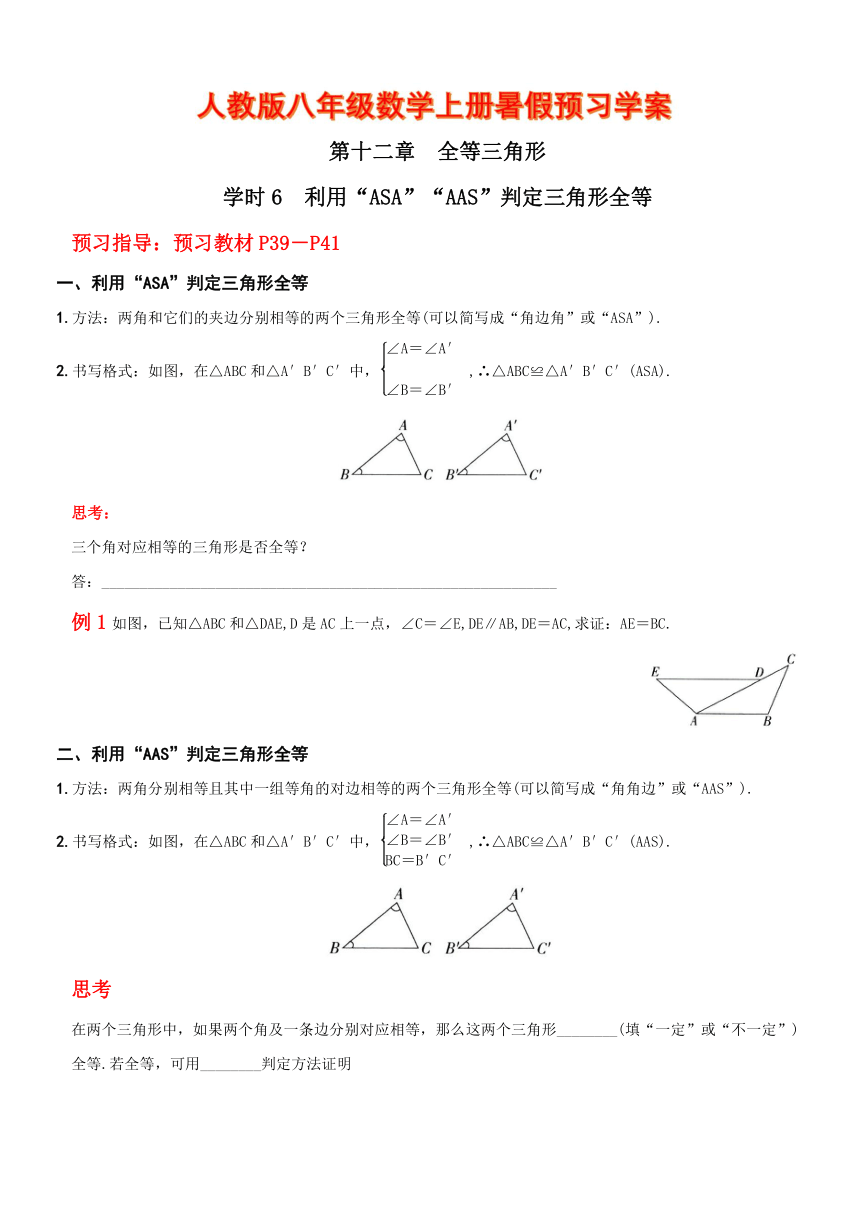 | |
| 格式 | docx | ||
| 文件大小 | 863.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 10:59:13 | ||
图片预览


文档简介
第十二章 全等三角形
学时6 利用“ASA”“AAS”判定三角形全等
预习指导:预习教材P39-P41
一、利用“ASA”判定三角形全等
1.方法:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
2.书写格式:如图,在△ABC和△A′B′C′中,
,∴△ABC≌△A′B′C′(ASA).
思考:
三个角对应相等的三角形是否全等?
答:____________________________________________________________
例1如图,已知△ABC和△DAE,D是AC上一点,∠C=∠E,DE∥AB,DE=AC,求证:AE=BC.
二、利用“AAS”判定三角形全等
1.方法:两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
2.书写格式:如图,在△ABC和△A′B′C′中,,∴△ABC≌△A′B′C′(AAS).
思考
在两个三角形中,如果两个角及一条边分别对应相等,那么这两个三角形________(填“一定”或“不一定”)全等.若全等,可用________判定方法证明
例2如图,D是△ABC的边AB上一点,AB∥FC,DF交AC于点E,DE=EF.求证:AE=CE
预习反馈
检验一下你的预习成果!
1.如图,在△ABC中,∠1=∠2,AD⊥BC于点D,则可得到△ABD≌△ACD,理由是 ( )
A.SSSB.SASC.ASAD.AAS
2.如图,各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是 ( )
A.甲和乙 B.只有乙 C.甲和丙 D.乙和丙
3.如图,AB=AC,AD=AE,BE,CD交于点O,则图中全等的三角形共有 ( )
A.0对 B.1对 C.2对 D.3对
4.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2,∠E=∠C,AE=AC,
∠ADE=60°,则∠B=________。
5.如图,已知∠CAE=∠BAD,AC=AD,要证明△ABC≌△AED.
(1)若以“SAS”为依据,还需添加的条件是:____________________;
(2)若以“AAS”为依据,还需添加的条件是:____________________;
(3)若以“ASA”为依据,还需添加的条件是:____________________。
6.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
求证:AC=CD.
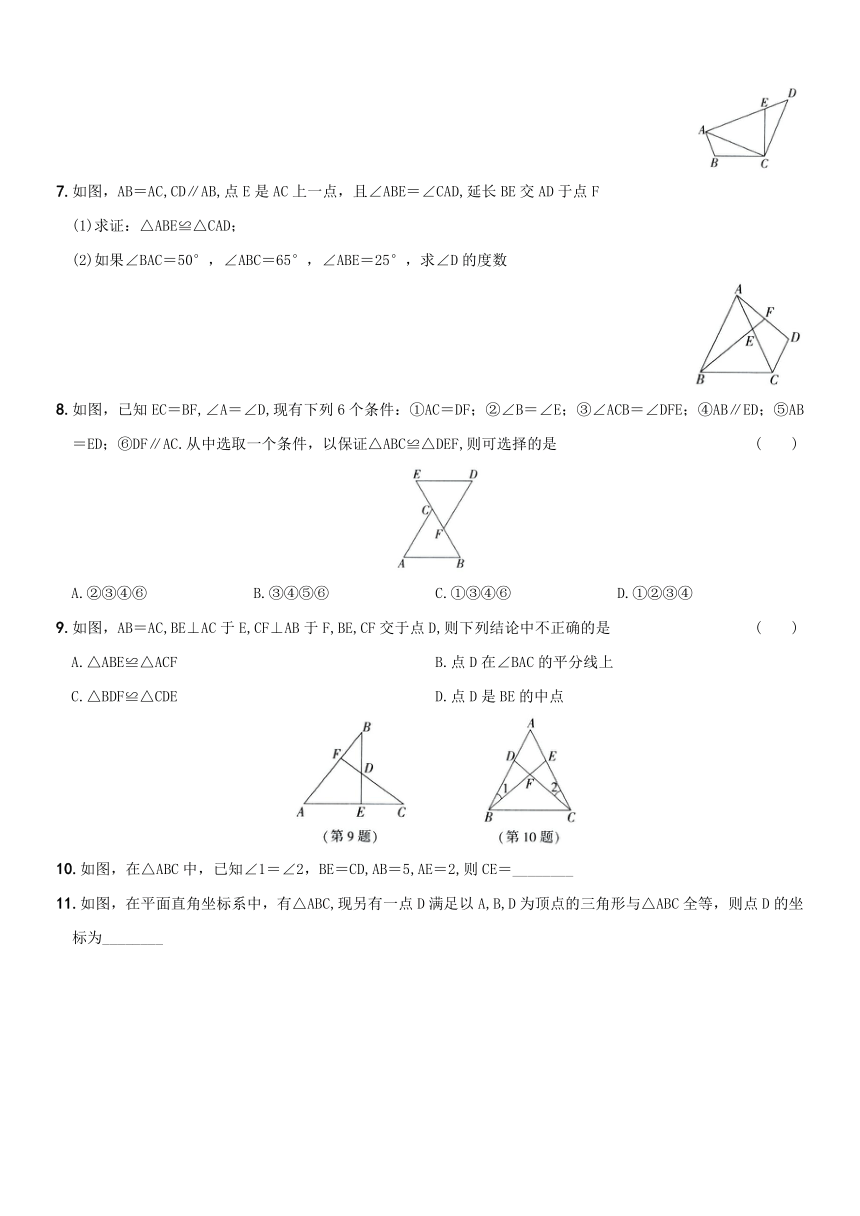
7.如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F
(1)求证:△ABE≌△CAD;
(2)如果∠BAC=50°,∠ABC=65°,∠ABE=25°,求∠D的度数
8.如图,已知EC=BF,∠A=∠D,现有下列6个条件:①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC.从中选取一个条件,以保证△ABC≌△DEF,则可选择的是 ( )
A.②③④⑥ B.③④⑤⑥ C.①③④⑥ D.①②③④
9.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于点D,则下列结论中不正确的是 ( )
A.△ABE≌△ACF B.点D在∠BAC的平分线上
C.△BDF≌△CDE D.点D是BE的中点
10.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=________
11.如图,在平面直角坐标系中,有△ABC,现另有一点D满足以A,B,D为顶点的三角形与△ABC全等,则点D的坐标为________
12.如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF,交AB于点E,连接EG,EF
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.
13.如图,在平面直角坐标系中有一点P(5,5),M(0,m)为y轴上任意一点,N为x轴上任意一点,且∠MPN=90°.
(1)如图①,当m=5时,OM+ON的值为________
(2)如图②,当0(3)如图③,探索:当m<0时,OM与ON的数量关系为________________。
【参考答案及解析】
学时6 利用“ASA”“AAS”判定三角形全等
【预习指导】
一、思考:不一定.
例1∵DE∥AB,∴∠ADE=∠BAC.
在△ADE和△BAC中,
,∴△ADE≌△BAC(ASA),∴AE=BC.
二、思考:一定 ASA或AAS
例2∵AB∥FC,∴∠A=∠ECF,∠ADE=∠F
在△ADE和△CFE中,,∴△ADE≌△CFE(AAS).∴AE=CE.
【预习反馈】
1.C 2.D 3.C 4.60°
5.(1)AB=AE (2)∠B=∠E (3)∠C=∠D
6.∵∠BCE=∠ACD=90°,∴∠BCA=∠ECD.
在△ABC和△DEC中,,∴△ABC≌△DEC(AAS),∴AC=CD.
7.(1)∵CD∥AB,∴∠BAE=∠ACD.∵AB=CA,∠ABE=∠CAD,∴△ABE≌△CAD(ASA).
(2)∠BAC=50°,∠ABE=∠CAD=25°,∴∠BAD=∠BAC+∠CAD=50°+25°=75°.ABCD,
∴∠D=180°-∠BAD=180°-75°=105°.
8.A
解析:∵EC=BF,∴EC+FC=BF+CF,即EF=BC.
∵∠A=∠D,结合②③,可利用AAS证得△ABC≌△DEF.由④AB∥ED可推出②,由⑥DF∥AC可推出
③,所以选②③④⑥,故选A.
9.D
解析:A.∵AB=AC,BE⊥AC于E,CF⊥AB于F,∠A=∠A,∴△ABE≌△ACF(AAS),正确;B.∵△ABE≌△ACF,AB=AC,∴BF=CE,∠B=∠C.CF⊥AB,BE⊥AC,∴∠DFB=∠DEC=90°,∴△BDF≌△CDE,∴DF=DE,故点D在∠BAC的平分线上,正确;由B知C正确;D.无法判定,错误,故选D.
10.3
解析:在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),
∴AD=AE=2,AC=AB=5,∴CE=BD=AB-AD=3.
11.(-2,-3),(4,3),(4,-3)
解析:点D的可能位置如图所示.
12.(1)∵AC∥BG,∴∠GBD=∠C.在△GBD与△FCD中,
,∴△GBD≌△FCD(ASA),∴BG=CF
(2)BE+CF>EF.理由:∵△GBD≌△FCD,∴GD=FD.
在△GDE与△FDE中,
,∴△GDE≌△FDE(SAS),
∴EG=EF.∵BE+BG>GE,∴BE+CF>EF.
13.(1)10
(2)当0(3)OM=ON-10
解析:作PA⊥y轴于A,PB⊥x轴于B,如图②所示.同(2)得△APM≌△BPN(ASA),
∴AM=BN,∴OM=AM-OA=BN-OA=ON-OB-OA=ON-10.
学时6 利用“ASA”“AAS”判定三角形全等
预习指导:预习教材P39-P41
一、利用“ASA”判定三角形全等
1.方法:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
2.书写格式:如图,在△ABC和△A′B′C′中,
,∴△ABC≌△A′B′C′(ASA).
思考:
三个角对应相等的三角形是否全等?
答:____________________________________________________________
例1如图,已知△ABC和△DAE,D是AC上一点,∠C=∠E,DE∥AB,DE=AC,求证:AE=BC.
二、利用“AAS”判定三角形全等
1.方法:两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
2.书写格式:如图,在△ABC和△A′B′C′中,,∴△ABC≌△A′B′C′(AAS).
思考
在两个三角形中,如果两个角及一条边分别对应相等,那么这两个三角形________(填“一定”或“不一定”)全等.若全等,可用________判定方法证明
例2如图,D是△ABC的边AB上一点,AB∥FC,DF交AC于点E,DE=EF.求证:AE=CE
预习反馈
检验一下你的预习成果!
1.如图,在△ABC中,∠1=∠2,AD⊥BC于点D,则可得到△ABD≌△ACD,理由是 ( )
A.SSSB.SASC.ASAD.AAS
2.如图,各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是 ( )
A.甲和乙 B.只有乙 C.甲和丙 D.乙和丙
3.如图,AB=AC,AD=AE,BE,CD交于点O,则图中全等的三角形共有 ( )
A.0对 B.1对 C.2对 D.3对
4.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2,∠E=∠C,AE=AC,
∠ADE=60°,则∠B=________。
5.如图,已知∠CAE=∠BAD,AC=AD,要证明△ABC≌△AED.
(1)若以“SAS”为依据,还需添加的条件是:____________________;
(2)若以“AAS”为依据,还需添加的条件是:____________________;
(3)若以“ASA”为依据,还需添加的条件是:____________________。
6.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
求证:AC=CD.
7.如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F
(1)求证:△ABE≌△CAD;
(2)如果∠BAC=50°,∠ABC=65°,∠ABE=25°,求∠D的度数
8.如图,已知EC=BF,∠A=∠D,现有下列6个条件:①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC.从中选取一个条件,以保证△ABC≌△DEF,则可选择的是 ( )
A.②③④⑥ B.③④⑤⑥ C.①③④⑥ D.①②③④
9.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于点D,则下列结论中不正确的是 ( )
A.△ABE≌△ACF B.点D在∠BAC的平分线上
C.△BDF≌△CDE D.点D是BE的中点
10.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=________
11.如图,在平面直角坐标系中,有△ABC,现另有一点D满足以A,B,D为顶点的三角形与△ABC全等,则点D的坐标为________
12.如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF,交AB于点E,连接EG,EF
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.
13.如图,在平面直角坐标系中有一点P(5,5),M(0,m)为y轴上任意一点,N为x轴上任意一点,且∠MPN=90°.
(1)如图①,当m=5时,OM+ON的值为________
(2)如图②,当0
【参考答案及解析】
学时6 利用“ASA”“AAS”判定三角形全等
【预习指导】
一、思考:不一定.
例1∵DE∥AB,∴∠ADE=∠BAC.
在△ADE和△BAC中,
,∴△ADE≌△BAC(ASA),∴AE=BC.
二、思考:一定 ASA或AAS
例2∵AB∥FC,∴∠A=∠ECF,∠ADE=∠F
在△ADE和△CFE中,,∴△ADE≌△CFE(AAS).∴AE=CE.
【预习反馈】
1.C 2.D 3.C 4.60°
5.(1)AB=AE (2)∠B=∠E (3)∠C=∠D
6.∵∠BCE=∠ACD=90°,∴∠BCA=∠ECD.
在△ABC和△DEC中,,∴△ABC≌△DEC(AAS),∴AC=CD.
7.(1)∵CD∥AB,∴∠BAE=∠ACD.∵AB=CA,∠ABE=∠CAD,∴△ABE≌△CAD(ASA).
(2)∠BAC=50°,∠ABE=∠CAD=25°,∴∠BAD=∠BAC+∠CAD=50°+25°=75°.ABCD,
∴∠D=180°-∠BAD=180°-75°=105°.
8.A
解析:∵EC=BF,∴EC+FC=BF+CF,即EF=BC.
∵∠A=∠D,结合②③,可利用AAS证得△ABC≌△DEF.由④AB∥ED可推出②,由⑥DF∥AC可推出
③,所以选②③④⑥,故选A.
9.D
解析:A.∵AB=AC,BE⊥AC于E,CF⊥AB于F,∠A=∠A,∴△ABE≌△ACF(AAS),正确;B.∵△ABE≌△ACF,AB=AC,∴BF=CE,∠B=∠C.CF⊥AB,BE⊥AC,∴∠DFB=∠DEC=90°,∴△BDF≌△CDE,∴DF=DE,故点D在∠BAC的平分线上,正确;由B知C正确;D.无法判定,错误,故选D.
10.3
解析:在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),
∴AD=AE=2,AC=AB=5,∴CE=BD=AB-AD=3.
11.(-2,-3),(4,3),(4,-3)
解析:点D的可能位置如图所示.
12.(1)∵AC∥BG,∴∠GBD=∠C.在△GBD与△FCD中,
,∴△GBD≌△FCD(ASA),∴BG=CF
(2)BE+CF>EF.理由:∵△GBD≌△FCD,∴GD=FD.
在△GDE与△FDE中,
,∴△GDE≌△FDE(SAS),
∴EG=EF.∵BE+BG>GE,∴BE+CF>EF.
13.(1)10
(2)当0
解析:作PA⊥y轴于A,PB⊥x轴于B,如图②所示.同(2)得△APM≌△BPN(ASA),
∴AM=BN,∴OM=AM-OA=BN-OA=ON-OB-OA=ON-10.
