2022-2023学年人教版八年级数学上册暑假预习 第十二章 学时7 利用“HL”判定三角形全等 学案(有答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册暑假预习 第十二章 学时7 利用“HL”判定三角形全等 学案(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 528.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 10:59:43 | ||
图片预览

文档简介
第十二章 全等三角形
学时7 利用“HL”判定三角形全等
预习指导:预习教材P41-P43
利用“HL”判定三角形全等
1.方法:斜边和一条直角边分别对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“H”).
2.书写格式:如图,在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△A′B′C′(HL).
思考
直角三角形是特殊的三角形,“H”是判定两个直角三角形全等特有的方法,对于一般三角形________(填“成立”或“不成立”).结合前面学习的判定方法可知:判定两个直角三角形全等共有________种方法
例 下列条件中不能判定两个直角三角形全等的是 ( )
A.一个锐角和一条斜边分别对应相等 B.两条直角边分别对应相等
C.一条直角边和一条斜边分别对应相等 D.两个锐角分别对应相等
预习反馈
检验一下你的预习成果
1.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到Rt△AOB≌Rt△COD,理由是 ( )
A.HL B.SAS C.ASA D.AAS
2.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是 ( )
A.∠ABC=∠ABD B.AC=AD C.∠BAC=∠BAD D.AC=BC
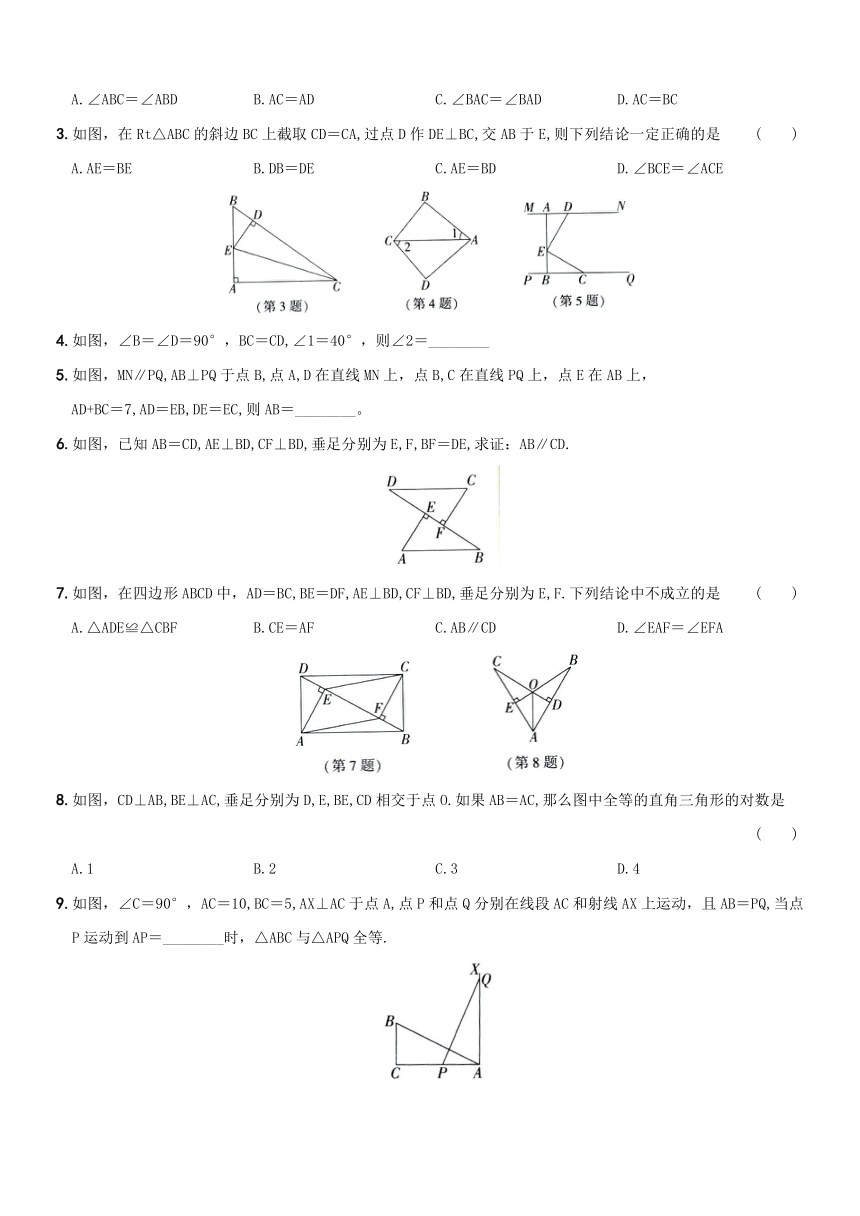
3.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是 ( )
A.AE=BE B.DB=DE C.AE=BD D.∠BCE=∠ACE
4.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=________
5.如图,MN∥PQ,AB⊥PQ于点B,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,
AD+BC=7,AD=EB,DE=EC,则AB=________。
6.如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD.
7.如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F.下列结论中不成立的是 ( )
A.△ADE≌△CBF B.CE=AF C.AB∥CD D.∠EAF=∠EFA
8.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
A.1 B.2 C.3 D.4
9.如图,∠C=90°,AC=10,BC=5,AX⊥AC于点A,点P和点Q分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=________时,△ABC与△APQ全等.
1O.如图,OA=OB,AC=BD,OA⊥AC,OB⊥BD,OM⊥CD于点M,求证:OM平分∠AOB.
11.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E,且AD=CE.
(1)若点B,C在DE的同侧(如图①所示),求证:AB⊥AC.
(2)若点B,C在DE的两侧(如图②所示),其他条件不变,AB与AC仍垂直吗?若垂直,请给出证明:若不垂直,请说明理由.
【参考答案及解析】
学时7 利用“HL”判定三角形全等
【预习指导】
思考:不成立 5
例D
【预习反馈】
1.A 2.B 3.D 4.50° 5.7
6.∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°.
∵BF=DE,∴BF+EF=DE+EF,∴BE=DF在Rt△AEB和Rt△CFD中,∴Rt△AEB≌Rt△CFD(HL),
∴∠B=∠D,∴AB∥CD.
7.D解析:∵AE⊥BD,CF⊥BD,∴∠DEA=∠CFB=90°.BE=DF,∴BE-EF=DF-EF,即BF=DE.在Rt△ADE和Rt△CBF中,,∴Rt△ADE≌Rt△CBF(HL),∴选项A成立;由Rt△ADE≌Rt△CBF,可得AE=CF,在△AEF和△CFE中,,∠AEF=∠CFE=90°,∴△AEF≌△CFE(SAS),∴AF=CE,∴选项B成立;由△AEF≌△CFE可得∠AFE=∠CEF,∴180°-∠AFE=180°-∠CEF,即∠AFB=∠CED,在△ABF和△CDE中,,∴△ABF≌△CDE,∴∠ABF=∠CDE,∴AB∥CD,∴选项C成立;D选项无法证得.故选D.
8.C
解析:BE⊥AC,CD⊥AB,∴∠ADC=∠AEB=90°.
,∴△ADC≌△AEB(AAS).∴AE=AD.
又AO=AO,∠ADC=∠AEB=90°,∴Rt△AOE≌Rt△AOD(HL).
∴OE=OD.∵∠COE=∠BOD,∠B=∠C,∴△COE≌△BOD(AAS).
共有3对直角三角形全等,故选C.
9.5或10
解析:∵AX⊥AC,∴∠PAQ=90°,∴∠C=∠PAQ.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△OPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在△ABC和△PQA中,,∴Rt△ABC≌Rt△PQA(HL).
综上所述,当点P运动到AP=5或10时,△ABC与△APQ全等.
10.如图,连接OC,OD.OA⊥AC,OB⊥BD,∴∠A=∠B
=90°.在△OAC和△OBD中,
∴△OAC≌△OBD(SAS),∴∠AOC=∠BOD,OC=OD.
∵OM⊥CD,∴∠OMC=∠OMD=90°.在Rt△OMC和Rt△OMD中,.∴Rt△OMC≌Rt△OMD(HL),
∴∠COM=∠DOM,
∴∠AOC+∠COM=∠BOD+∠DOM,即∠AOM=∠BOM,即OM平分∠AOB.
11.(1)∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°.在Rt△ABD和Rt△CAE中,
∵.Rt△ABD≌Rt△CAE(HL).∴∠DBA=∠CAE.∵∠DAB+∠DBA=90°,
∴∠BAD+∠CAE=90°.∴∠BAC=180°-(∠BAD+∠CAE)=90°,∴AB⊥AC.
(2)AB与AC仍垂直.证明:同(1)可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA.∠CAE+∠ECA=90°,
∴∠CAE+∠DAB=90°,即∠BAC=90°,∴AB⊥AC.
学时7 利用“HL”判定三角形全等
预习指导:预习教材P41-P43
利用“HL”判定三角形全等
1.方法:斜边和一条直角边分别对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“H”).
2.书写格式:如图,在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△A′B′C′(HL).
思考
直角三角形是特殊的三角形,“H”是判定两个直角三角形全等特有的方法,对于一般三角形________(填“成立”或“不成立”).结合前面学习的判定方法可知:判定两个直角三角形全等共有________种方法
例 下列条件中不能判定两个直角三角形全等的是 ( )
A.一个锐角和一条斜边分别对应相等 B.两条直角边分别对应相等
C.一条直角边和一条斜边分别对应相等 D.两个锐角分别对应相等
预习反馈
检验一下你的预习成果
1.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到Rt△AOB≌Rt△COD,理由是 ( )
A.HL B.SAS C.ASA D.AAS
2.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是 ( )
A.∠ABC=∠ABD B.AC=AD C.∠BAC=∠BAD D.AC=BC
3.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是 ( )
A.AE=BE B.DB=DE C.AE=BD D.∠BCE=∠ACE
4.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=________
5.如图,MN∥PQ,AB⊥PQ于点B,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,
AD+BC=7,AD=EB,DE=EC,则AB=________。
6.如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD.
7.如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F.下列结论中不成立的是 ( )
A.△ADE≌△CBF B.CE=AF C.AB∥CD D.∠EAF=∠EFA
8.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
A.1 B.2 C.3 D.4
9.如图,∠C=90°,AC=10,BC=5,AX⊥AC于点A,点P和点Q分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=________时,△ABC与△APQ全等.
1O.如图,OA=OB,AC=BD,OA⊥AC,OB⊥BD,OM⊥CD于点M,求证:OM平分∠AOB.
11.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E,且AD=CE.
(1)若点B,C在DE的同侧(如图①所示),求证:AB⊥AC.
(2)若点B,C在DE的两侧(如图②所示),其他条件不变,AB与AC仍垂直吗?若垂直,请给出证明:若不垂直,请说明理由.
【参考答案及解析】
学时7 利用“HL”判定三角形全等
【预习指导】
思考:不成立 5
例D
【预习反馈】
1.A 2.B 3.D 4.50° 5.7
6.∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°.
∵BF=DE,∴BF+EF=DE+EF,∴BE=DF在Rt△AEB和Rt△CFD中,∴Rt△AEB≌Rt△CFD(HL),
∴∠B=∠D,∴AB∥CD.
7.D解析:∵AE⊥BD,CF⊥BD,∴∠DEA=∠CFB=90°.BE=DF,∴BE-EF=DF-EF,即BF=DE.在Rt△ADE和Rt△CBF中,,∴Rt△ADE≌Rt△CBF(HL),∴选项A成立;由Rt△ADE≌Rt△CBF,可得AE=CF,在△AEF和△CFE中,,∠AEF=∠CFE=90°,∴△AEF≌△CFE(SAS),∴AF=CE,∴选项B成立;由△AEF≌△CFE可得∠AFE=∠CEF,∴180°-∠AFE=180°-∠CEF,即∠AFB=∠CED,在△ABF和△CDE中,,∴△ABF≌△CDE,∴∠ABF=∠CDE,∴AB∥CD,∴选项C成立;D选项无法证得.故选D.
8.C
解析:BE⊥AC,CD⊥AB,∴∠ADC=∠AEB=90°.
,∴△ADC≌△AEB(AAS).∴AE=AD.
又AO=AO,∠ADC=∠AEB=90°,∴Rt△AOE≌Rt△AOD(HL).
∴OE=OD.∵∠COE=∠BOD,∠B=∠C,∴△COE≌△BOD(AAS).
共有3对直角三角形全等,故选C.
9.5或10
解析:∵AX⊥AC,∴∠PAQ=90°,∴∠C=∠PAQ.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△OPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在△ABC和△PQA中,,∴Rt△ABC≌Rt△PQA(HL).
综上所述,当点P运动到AP=5或10时,△ABC与△APQ全等.
10.如图,连接OC,OD.OA⊥AC,OB⊥BD,∴∠A=∠B
=90°.在△OAC和△OBD中,
∴△OAC≌△OBD(SAS),∴∠AOC=∠BOD,OC=OD.
∵OM⊥CD,∴∠OMC=∠OMD=90°.在Rt△OMC和Rt△OMD中,.∴Rt△OMC≌Rt△OMD(HL),
∴∠COM=∠DOM,
∴∠AOC+∠COM=∠BOD+∠DOM,即∠AOM=∠BOM,即OM平分∠AOB.
11.(1)∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°.在Rt△ABD和Rt△CAE中,
∵.Rt△ABD≌Rt△CAE(HL).∴∠DBA=∠CAE.∵∠DAB+∠DBA=90°,
∴∠BAD+∠CAE=90°.∴∠BAC=180°-(∠BAD+∠CAE)=90°,∴AB⊥AC.
(2)AB与AC仍垂直.证明:同(1)可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA.∠CAE+∠ECA=90°,
∴∠CAE+∠DAB=90°,即∠BAC=90°,∴AB⊥AC.
