2022-2023学年人教版八年级数学上册暑假预习 第十二章 全等三角形(章节综合自测) 学案(有答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册暑假预习 第十二章 全等三角形(章节综合自测) 学案(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 823.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 00:00:00 | ||
图片预览



文档简介
第十二章 全等三角形(章节综合自测)
(时间:60分钟,满分:100分) 得分:________
一、选择题(每小题3分,共24分)
1.下列每组图形中,是全等形的是 ( )
2.如图,△ACE≌△DBF,AB=3,BC=2,则AD的长度等于 ( )
A.2 B.5 C.8 D.10
3.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法便可得△NOC≌△MOC,其依据是 ( )
A.SSS B.SAS C.ASA D.AAS
4.在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠B′;⑥∠C=∠C′.则下列条件组不能保证△ABC≌△A′B′C′的是 ( )
A.①②③ B.①②⑤ C.②④⑤ D.①③⑤
5.如图,AC=BD,∠CAB=∠DBA,∠ABC=20°,则∠COA的度数为 ( )
A.10° B.20° C.40° D.90°
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是 ( )
A.15 B.30 C.45 D.60
7.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是 ( )
A.AC B.AF C.CF D.EF
8.如图,点A,B分别是∠NOP,∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,则以下结论错误的是 ( )
A.AD+BC=AB B.∠AOB=90°
C.与∠CBO互余的角有2个 D.点O是CD的中点
二、填空题(每小题4分,共24分)
9.如图,△ACB≌△A′CB′,∠BCA′=35°,∠B′CA′=65°,则∠ACA′的度数为________
10.如图,在△ABC中,AB=AC,点E,D分别在AB,AC上,不再添加其他辅助线,添加一个条件________,使BD=CE.(只添一个即可)
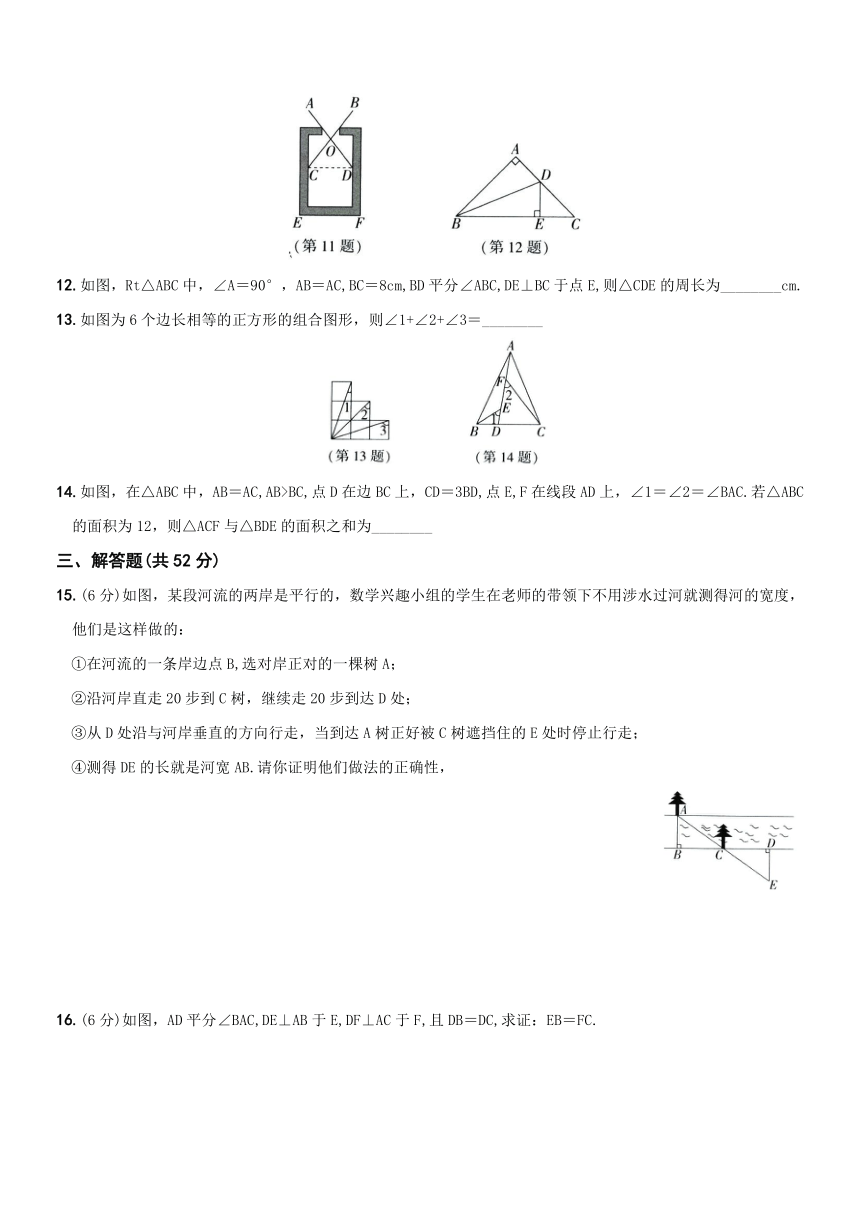
11.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,则圆形容器的壁厚是________
12.如图,Rt△ABC中,∠A=90°,AB=AC,BC=8cm,BD平分∠ABC,DE⊥BC于点E,则△CDE的周长为________cm.
13.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=________
14.如图,在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=3BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ACF与△BDE的面积之和为________
三、解答题(共52分)
15.(6分)如图,某段河流的两岸是平行的,数学兴趣小组的学生在老师的带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边点B,选对岸正对的一棵树A;
②沿河岸直走20步到C树,继续走20步到达D处;
③从D处沿与河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长就是河宽AB.请你证明他们做法的正确性,
16.(6分)如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC.
17.(8分)如图,已知AB=AC,AD=AE,BD=CE. 求证:∠3=∠1+∠2.
18.(10分)如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD,CE有何特殊位置关系,并证明.
19.(10分)如图,BE⊥CE,BA∥CD,点E为AD的中点.求证:CE平分∠BCD.
20.(12分)【方法引入】在解决几何线段相等问题时,当条件中遇到角平分线时,经常采用下面构造全等三角形的解决思路:
如图①中,若C是∠MON的平分线OP上一点,点A在OM上,此时,在ON上截取OB=OA,连接BC,根据三角形全等判定方法:________,容易构造出全等三角形△OBC和△OAC,从而得到线段CA与CB相等.(写出完整的证明过程)
【学以致用】参考上述学到的知识,解答下列问题:
如图②,在△ABC中,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.求证:FE=FD.
【参考答案及解析】
第十二章自测卷
1.C 2.C 3.A 4.D 5.C 6.B
7.D
解析:∠ACB+∠FCE=180°-∠ACF=120°,又∵∠BAC+∠ACB=180°-∠B=120°,∴∠FCE=∠BAC.在△ABC与△CEF中,∠BAC=∠ECF,AB=CE,∠B=∠E,∴△ABC≌△CEF,∴BC=EF.故选D.
8.C
解析:点A,B分别是∠NOP,∠MOP平分线上的点,∴AD=AE,BC=BE.AB=AE+BE,∴AB=AD+BC,∴A选项正确;在Rt△AOD和Rt△AOE中,Rt△AOD≌Rt△AOE(HL),∴OD=OE,同理可得OC=OE,又∠AOE=∠AOD,∠BOC=∠BOE,
∴∠AOB=×180°=90°,∴B选项正确;与∠CBO互余的角有∠COB,∠EOB,∠OAD,∠OAE,共4个,∴C选项错误;∵OC=OD=OE,∴点O是CD的中点,∴D选项正确.故选C.
9.30°
10.答案不唯一,如:AE=AD
11.(b-a)
12.8
13.135°
14.3
15.在Rt△ABC和Rt△EDC中,,
∴Rt△ABC≌Rt△EDC(ASA),∴AB=ED.即他们的做法是正确的.
16.∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,∴DE=DF.在Rt△DBE和Rt△DCF中,
Rt△DBE≌Rt△DCF(HL),∴EB=FC.
17.在△ABD和△ACE中,∴△ABD≌△ACE(SSS),
∴∠BAD=∠1,∠ABD=∠2.∵∠3=∠BAD+∠ABD,∴∠3=∠1+∠2.
18.(1)∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS).
(2)BD⊥CE.证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.∵∠DAE=90°,∴∠E+∠ADE=90°,
∴∠ADB+∠ADE=90°,即∠BDE=90°.∴BD⊥CE.
19.如图,延长BE,CD交于点F,BACD,∴∠A=∠ADF点E为AD的中点,
∴AE=ED.在△ABE和
△DFE中,,∴△ABE≌△DFE(ASA),∴BE=FE,
在△CEB和△CEF中,,
∴△CEB≌△CEF(SAS),∴∠BCE=∠FCE,即CE平分∠BCD.
20.【方法引入】SAS
证明如下:在ON上截取OB=OA,连接BC.
∵OC是∠MON的平分线,∴∠AOC=∠BOC.
在△AOC和△BOC中,OA=OB,∠AOC=∠BOC,OC=OC,
∴△AOC≌△BOC,∴CA=CB.
【学以致用】如图,在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,∴∠1=∠2.
在△AEF和△AGF中,
,∴△AEF≌△AGF(SAS),
∴∠AFE=∠AFG,FE=FG.
∵∠B=60°,∴∠BAC+∠ACB=180°-60°=120°.
∵AD,CE分别是∠BAC,∠BCA的平分线,∴∠2=∠BAC,∠3=∠ACB,
∴∠2+∠3=(∠BAC+∠ACB)=×120°=60°,
∴∠AFE=∠CFD=∠AFG=60.
∴∠CFG=180°-∠AFG-∠CFD=180°-60°-60°=60°,
∴∠CFG=∠CFD.
∵CE是∠BCA的平分线,∴∠3=∠4.
在△CFG和△CFD中,
,
∴△CFG≌△CFD(ASA),∴FG=FD,∴FE=FD.
(时间:60分钟,满分:100分) 得分:________
一、选择题(每小题3分,共24分)
1.下列每组图形中,是全等形的是 ( )
2.如图,△ACE≌△DBF,AB=3,BC=2,则AD的长度等于 ( )
A.2 B.5 C.8 D.10
3.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法便可得△NOC≌△MOC,其依据是 ( )
A.SSS B.SAS C.ASA D.AAS
4.在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠B′;⑥∠C=∠C′.则下列条件组不能保证△ABC≌△A′B′C′的是 ( )
A.①②③ B.①②⑤ C.②④⑤ D.①③⑤
5.如图,AC=BD,∠CAB=∠DBA,∠ABC=20°,则∠COA的度数为 ( )
A.10° B.20° C.40° D.90°
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是 ( )
A.15 B.30 C.45 D.60
7.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是 ( )
A.AC B.AF C.CF D.EF
8.如图,点A,B分别是∠NOP,∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,则以下结论错误的是 ( )
A.AD+BC=AB B.∠AOB=90°
C.与∠CBO互余的角有2个 D.点O是CD的中点
二、填空题(每小题4分,共24分)
9.如图,△ACB≌△A′CB′,∠BCA′=35°,∠B′CA′=65°,则∠ACA′的度数为________
10.如图,在△ABC中,AB=AC,点E,D分别在AB,AC上,不再添加其他辅助线,添加一个条件________,使BD=CE.(只添一个即可)
11.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,则圆形容器的壁厚是________
12.如图,Rt△ABC中,∠A=90°,AB=AC,BC=8cm,BD平分∠ABC,DE⊥BC于点E,则△CDE的周长为________cm.
13.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=________
14.如图,在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=3BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ACF与△BDE的面积之和为________
三、解答题(共52分)
15.(6分)如图,某段河流的两岸是平行的,数学兴趣小组的学生在老师的带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边点B,选对岸正对的一棵树A;
②沿河岸直走20步到C树,继续走20步到达D处;
③从D处沿与河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长就是河宽AB.请你证明他们做法的正确性,
16.(6分)如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC.
17.(8分)如图,已知AB=AC,AD=AE,BD=CE. 求证:∠3=∠1+∠2.
18.(10分)如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD,CE有何特殊位置关系,并证明.
19.(10分)如图,BE⊥CE,BA∥CD,点E为AD的中点.求证:CE平分∠BCD.
20.(12分)【方法引入】在解决几何线段相等问题时,当条件中遇到角平分线时,经常采用下面构造全等三角形的解决思路:
如图①中,若C是∠MON的平分线OP上一点,点A在OM上,此时,在ON上截取OB=OA,连接BC,根据三角形全等判定方法:________,容易构造出全等三角形△OBC和△OAC,从而得到线段CA与CB相等.(写出完整的证明过程)
【学以致用】参考上述学到的知识,解答下列问题:
如图②,在△ABC中,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.求证:FE=FD.
【参考答案及解析】
第十二章自测卷
1.C 2.C 3.A 4.D 5.C 6.B
7.D
解析:∠ACB+∠FCE=180°-∠ACF=120°,又∵∠BAC+∠ACB=180°-∠B=120°,∴∠FCE=∠BAC.在△ABC与△CEF中,∠BAC=∠ECF,AB=CE,∠B=∠E,∴△ABC≌△CEF,∴BC=EF.故选D.
8.C
解析:点A,B分别是∠NOP,∠MOP平分线上的点,∴AD=AE,BC=BE.AB=AE+BE,∴AB=AD+BC,∴A选项正确;在Rt△AOD和Rt△AOE中,Rt△AOD≌Rt△AOE(HL),∴OD=OE,同理可得OC=OE,又∠AOE=∠AOD,∠BOC=∠BOE,
∴∠AOB=×180°=90°,∴B选项正确;与∠CBO互余的角有∠COB,∠EOB,∠OAD,∠OAE,共4个,∴C选项错误;∵OC=OD=OE,∴点O是CD的中点,∴D选项正确.故选C.
9.30°
10.答案不唯一,如:AE=AD
11.(b-a)
12.8
13.135°
14.3
15.在Rt△ABC和Rt△EDC中,,
∴Rt△ABC≌Rt△EDC(ASA),∴AB=ED.即他们的做法是正确的.
16.∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,∴DE=DF.在Rt△DBE和Rt△DCF中,
Rt△DBE≌Rt△DCF(HL),∴EB=FC.
17.在△ABD和△ACE中,∴△ABD≌△ACE(SSS),
∴∠BAD=∠1,∠ABD=∠2.∵∠3=∠BAD+∠ABD,∴∠3=∠1+∠2.
18.(1)∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS).
(2)BD⊥CE.证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.∵∠DAE=90°,∴∠E+∠ADE=90°,
∴∠ADB+∠ADE=90°,即∠BDE=90°.∴BD⊥CE.
19.如图,延长BE,CD交于点F,BACD,∴∠A=∠ADF点E为AD的中点,
∴AE=ED.在△ABE和
△DFE中,,∴△ABE≌△DFE(ASA),∴BE=FE,
在△CEB和△CEF中,,
∴△CEB≌△CEF(SAS),∴∠BCE=∠FCE,即CE平分∠BCD.
20.【方法引入】SAS
证明如下:在ON上截取OB=OA,连接BC.
∵OC是∠MON的平分线,∴∠AOC=∠BOC.
在△AOC和△BOC中,OA=OB,∠AOC=∠BOC,OC=OC,
∴△AOC≌△BOC,∴CA=CB.
【学以致用】如图,在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,∴∠1=∠2.
在△AEF和△AGF中,
,∴△AEF≌△AGF(SAS),
∴∠AFE=∠AFG,FE=FG.
∵∠B=60°,∴∠BAC+∠ACB=180°-60°=120°.
∵AD,CE分别是∠BAC,∠BCA的平分线,∴∠2=∠BAC,∠3=∠ACB,
∴∠2+∠3=(∠BAC+∠ACB)=×120°=60°,
∴∠AFE=∠CFD=∠AFG=60.
∴∠CFG=180°-∠AFG-∠CFD=180°-60°-60°=60°,
∴∠CFG=∠CFD.
∵CE是∠BCA的平分线,∴∠3=∠4.
在△CFG和△CFD中,
,
∴△CFG≌△CFD(ASA),∴FG=FD,∴FE=FD.
