安徽省宿州市埇桥区宿城第一初级中学2021-2022学年七年级下学期期末考试 数学试卷(word版含答案)
文档属性
| 名称 | 安徽省宿州市埇桥区宿城第一初级中学2021-2022学年七年级下学期期末考试 数学试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 18:10:23 | ||
图片预览


文档简介
宿城第一初级中学2021—2022学年度第二学期期末质量检测
七年级数学试题卷
考试时间:100分钟 满分:120分
一、填空题(每小题3分,共30分)
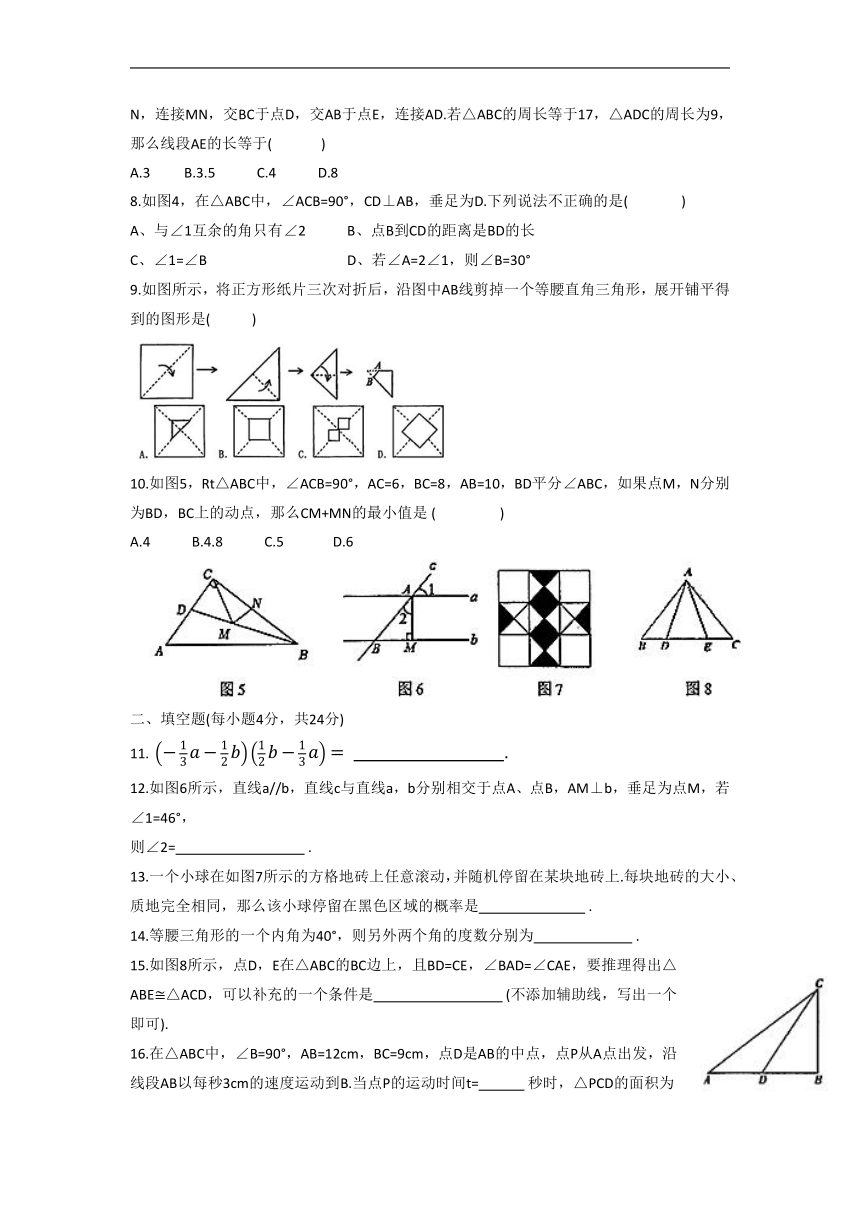
1.下列运算正确的是( )
A. B.2 C. D.
2.在下列长度的四根木棒中,能与5cm、7cm长的两根木棒钉成一个三角形的是( )
A.2cm B.8cm C.12cm D.13cm
3.下列事件是必然事件的是( )
A.乘坐公共汽车恰好有空座 B.同位角相等
C.打开手机就有未接电话 D.三角形内角和等于180°
4.如图1,在下列条件中,不能证明△ABD△ACD的是( )
A.BD=DC,AB=AC B.∠B=∠C,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠ADB=∠ADC,BD=DC
5.小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地.下列函数图象能表达这一过程的是( )
6.将一副三角板如图2放置,使点A落在DE上,若BC∥DE,则∠EFB的度数为 ( )
A.55° B.65° C.75° D.85°
7.如图3,在△ABC中,分别以点A和点B为圆心,大于 AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于17,△ADC的周长为9,那么线段AE的长等于( )
A.3 B.3.5 C.4 D.8
8.如图4,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )
A、与∠1互余的角只有∠2 B、点B到CD的距离是BD的长
C、∠1=∠B D、若∠A=2∠1,则∠B=30°
9.如图所示,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是( )
10.如图5,Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,BD平分∠ABC,如果点M,N分别为BD,BC上的动点,那么CM+MN的最小值是 ( )
A.4 B.4.8 C.5 D.6
二、填空题(每小题4分,共24分)
11. .
12.如图6所示,直线a//b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=46°,
则∠2= .
13.一个小球在如图7所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
14.等腰三角形的一个内角为40°,则另外两个角的度数分别为 .
15.如图8所示,点D,E在△ABC的BC边上,且BD=CE,∠BAD=∠CAE,要推理得出△ABE△ACD,可以补充的一个条件是 (不添加辅助线,写出一个即可).
16.在△ABC中,∠B=90°,AB=12cm,BC=9cm,点D是AB的中点,点P从A点出发,沿线段AB以每秒3cm的速度运动到B.当点P的运动时间t= 秒时,△PCD的面积为6cm2.
三、解答题(共66分)
17.(每小题5分,共10分)
(1)计算:
(2)先化简,再求值:其中
18.(8分)如图,已知 AC∥DF.直线AF分别与直线BD、CE相交于点G,H.
∠1=∠2,
求证:∠C=∠D.
解:∵∠1=∠2(已知)2
∠1=∠DGH( )
∴∠2= (等量代换)
∴ ∥ (同位角相等,两直线平行)
∴∠C= (两直线平行,同位角相等)
又∵AC∥DF( )
∴∠D=∠ABG ( )
∴∠C=∠D ( )
19.(8分)如图,某品牌自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形,填写下表:
链条节数/x(节) 2 3 4 . . .
链条长度/y(cm) 4.2 . . .
(2)请你写出y与x之间的关系式;
(3)如果一辆自行车的链条(安装前)共由50节链条组成,那么链条的总长度是多少
20.(8分)如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与 △ABC关于直线l成轴对称的 △AB′C′;
(2)△ABC的面积为 ;
21.(8分)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出 m(m>1)个红球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A 必然事件 随机事件
m的值
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出一个球是黑球的概率等于 ,求m的值.
22.(12分)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数。
23.(12分)如图,将两块含 45°角的大小不同的直角三角板△COD 和 △AOB如图①摆放,连结AC,BD.
(1)如图①,猜想线段AC与BD存在怎样的数量关系和位置关系,请写出结论并证明:
(2)将图①中的 △COD绕点0顺时针旋转一定的角度(如图②),连结AC,BD,其他条件不变,线段AC与BD还存在(1)中的关系吗 请写出结论并说明理由.
(3)将图①中的 △COD绕点0逆时针旋转一定的角度(如图③),连结AC,BD,其他条件不变,线段AC与BD存在怎样的关系 请直接写出结论.
七年级数学试题卷
考试时间:100分钟 满分:120分
一、填空题(每小题3分,共30分)
1.下列运算正确的是( )
A. B.2 C. D.
2.在下列长度的四根木棒中,能与5cm、7cm长的两根木棒钉成一个三角形的是( )
A.2cm B.8cm C.12cm D.13cm
3.下列事件是必然事件的是( )
A.乘坐公共汽车恰好有空座 B.同位角相等
C.打开手机就有未接电话 D.三角形内角和等于180°
4.如图1,在下列条件中,不能证明△ABD△ACD的是( )
A.BD=DC,AB=AC B.∠B=∠C,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠ADB=∠ADC,BD=DC
5.小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地.下列函数图象能表达这一过程的是( )
6.将一副三角板如图2放置,使点A落在DE上,若BC∥DE,则∠EFB的度数为 ( )
A.55° B.65° C.75° D.85°
7.如图3,在△ABC中,分别以点A和点B为圆心,大于 AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于17,△ADC的周长为9,那么线段AE的长等于( )
A.3 B.3.5 C.4 D.8
8.如图4,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )
A、与∠1互余的角只有∠2 B、点B到CD的距离是BD的长
C、∠1=∠B D、若∠A=2∠1,则∠B=30°
9.如图所示,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是( )
10.如图5,Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,BD平分∠ABC,如果点M,N分别为BD,BC上的动点,那么CM+MN的最小值是 ( )
A.4 B.4.8 C.5 D.6
二、填空题(每小题4分,共24分)
11. .
12.如图6所示,直线a//b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=46°,
则∠2= .
13.一个小球在如图7所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
14.等腰三角形的一个内角为40°,则另外两个角的度数分别为 .
15.如图8所示,点D,E在△ABC的BC边上,且BD=CE,∠BAD=∠CAE,要推理得出△ABE△ACD,可以补充的一个条件是 (不添加辅助线,写出一个即可).
16.在△ABC中,∠B=90°,AB=12cm,BC=9cm,点D是AB的中点,点P从A点出发,沿线段AB以每秒3cm的速度运动到B.当点P的运动时间t= 秒时,△PCD的面积为6cm2.
三、解答题(共66分)
17.(每小题5分,共10分)
(1)计算:
(2)先化简,再求值:其中
18.(8分)如图,已知 AC∥DF.直线AF分别与直线BD、CE相交于点G,H.
∠1=∠2,
求证:∠C=∠D.
解:∵∠1=∠2(已知)2
∠1=∠DGH( )
∴∠2= (等量代换)
∴ ∥ (同位角相等,两直线平行)
∴∠C= (两直线平行,同位角相等)
又∵AC∥DF( )
∴∠D=∠ABG ( )
∴∠C=∠D ( )
19.(8分)如图,某品牌自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形,填写下表:
链条节数/x(节) 2 3 4 . . .
链条长度/y(cm) 4.2 . . .
(2)请你写出y与x之间的关系式;
(3)如果一辆自行车的链条(安装前)共由50节链条组成,那么链条的总长度是多少
20.(8分)如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与 △ABC关于直线l成轴对称的 △AB′C′;
(2)△ABC的面积为 ;
21.(8分)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出 m(m>1)个红球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A 必然事件 随机事件
m的值
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出一个球是黑球的概率等于 ,求m的值.
22.(12分)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数。
23.(12分)如图,将两块含 45°角的大小不同的直角三角板△COD 和 △AOB如图①摆放,连结AC,BD.
(1)如图①,猜想线段AC与BD存在怎样的数量关系和位置关系,请写出结论并证明:
(2)将图①中的 △COD绕点0顺时针旋转一定的角度(如图②),连结AC,BD,其他条件不变,线段AC与BD还存在(1)中的关系吗 请写出结论并说明理由.
(3)将图①中的 △COD绕点0逆时针旋转一定的角度(如图③),连结AC,BD,其他条件不变,线段AC与BD存在怎样的关系 请直接写出结论.
同课章节目录
