人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共29张ppt)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 15:14:02 | ||
图片预览







文档简介
(共29张PPT)
空间向量及其线性运算
一、空间向量的有关概念
情景引入
这是一个做滑翔伞运动的场景.可以想象,在滑翔过程中,飞行员会受到来自不同方向、大小各异的力.
一、空间向量的有关概念
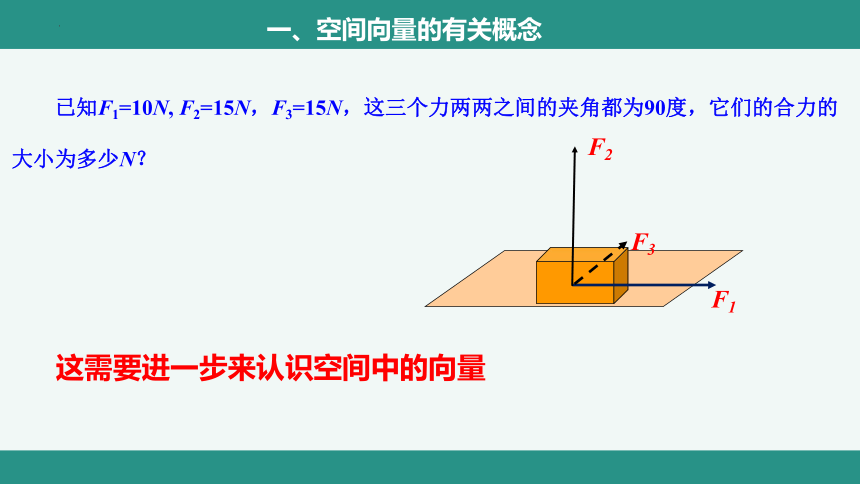
已知F1=10N, F2=15N,F3=15N,这三个力两两之间的夹角都为90度,它们的合力的大小为多少N?
F3
F1
F2
这需要进一步来认识空间中的向量
一、空间向量的有关概念
起点
终点
一、空间向量的有关概念
定义:
既有大小又有方向的量。
表示
几何表示法:有向线段
符号表示法:
a ,b
AB
长度(模)
平面向量是什么?如何表示平面向量?你能类比平面向量和表示给出空间向量的概念和空间向量的表示吗?
向量的大小,记作
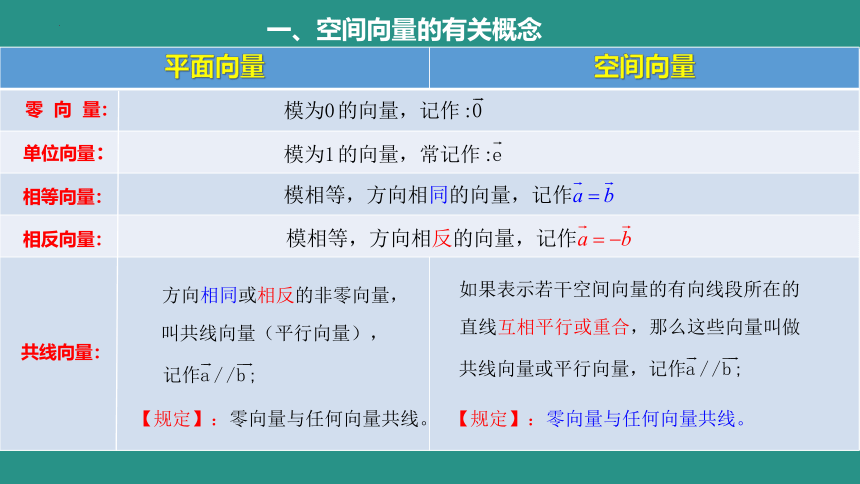
平面向量 空间向量
零 向 量:
单位向量:
相反向量:
相等向量:
共线向量:
一、空间向量的有关概念
解 (2)A为假命题,根据向量相等的定义知,两向量相等,不仅模要相等,而且还要方向相同,而A中向
量a与b的方向不一定相同;
√
解(1)A中,单位向量长度相等,方向不确定;B中,|a|=|b|只能说明a,b的长度相等而方向不确定;
C中,向量不能比较大小.
一、空间向量的有关概念
C为真命题,向量的相等满足传递性;D为假命题,平行向量不一定具有传递性,当b=0时,a与c不
一定平行.
√
√
【练1】如图所示,以长方体ABCD-A1B1C1D1的八个顶点的两点为起点和终点的向量中,
一、空间向量的有关概念
二、空间向量的线性运算及其运算律
运算:空间向量的加法、减法、数乘向量的定义与平面向量的运算一样
运算律:⑴加法交换律:
⑵加法结合律:
⑶数乘分配律:
二、空间向量的线性运算及其运算律
几点注意 :
⑵首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量.即:
⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
⑶两个向量相加的平行四边形法则在空间仍然成立.
二、空间向量的线性运算及其运算律
√
例2 (多选)如图,在正方体ABCD -A1B1C1D1中,下列各式运算结果为 的是( )
√
二、空间向量的线性运算及其运算律
0
解 方法一(转化为加法运算)
方法二(转化为减法运算)
二、空间向量的线性运算及其运算律
解(1)∵P是C1D1的中点,
二、空间向量的线性运算及其运算律
解(2)∵N是BC的中点,
二、空间向量的线性运算及其运算律
解(3)∵M是AA1的中点,
二、空间向量的线性运算及其运算律
《二》利用数乘运算进行向量表示的技巧
二、空间向量的线性运算及其运算律
(1)用反向量:向量的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.
(2)用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,
必要时可采用空间向量的自由平移获得运算结果.
【悟】 《一》空间向量加法、减法运算的两个技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量
转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
二、空间向量的线性运算及其运算律
【练2】如图,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,
请化简以下式子,并在图中标出化简结果.
二、空间向量的线性运算及其运算律
【练3】已知四边形ABCD为正方形,P是四边形ABCD所在平面外一点,P在平面ABCD上
的射影恰好是正方形的中心O,Q是CD的中点,求下列各题中x,y的值.
∴x=2,y=-2.
三、共线定理、共面定理及其应用
共线向量
【规定】:零向量与任意向量共线.
三、共线定理、共面定理及其应用
共线定理
O
A
B
P
a
O
A
B
P
a
我们知道,任意两个空间向量总是共面的,但三个空间向量
既可能是共面的,也可能是不共面的。
O
A
l
三、共线定理、共面定理及其应用
共面向量
那么,什么情况下三个空间向量共面呢?
三、共线定理、共面定理及其应用
共面定理
O
A
C
B
三、共线定理、共面定理及其应用
共面定理
O
A
C
B
α
三、共线定理、共面定理及其应用
共面定理
O
A
B
C
D
E
F
G
H
三、共线定理、共面定理及其应用
1、空间向量的概念
课堂小结
2、空间向量的运算
3 、共线向量(平行向量)的概念及空间向量共线的充要条件
4、共面向量的概念及向量共面的充要条件
作业:
课本P5-6 练习1,2,3,4,5
本课结束
“
”
空间向量及其线性运算
一、空间向量的有关概念
情景引入
这是一个做滑翔伞运动的场景.可以想象,在滑翔过程中,飞行员会受到来自不同方向、大小各异的力.
一、空间向量的有关概念
已知F1=10N, F2=15N,F3=15N,这三个力两两之间的夹角都为90度,它们的合力的大小为多少N?
F3
F1
F2
这需要进一步来认识空间中的向量
一、空间向量的有关概念
起点
终点
一、空间向量的有关概念
定义:
既有大小又有方向的量。
表示
几何表示法:有向线段
符号表示法:
a ,b
AB
长度(模)
平面向量是什么?如何表示平面向量?你能类比平面向量和表示给出空间向量的概念和空间向量的表示吗?
向量的大小,记作
平面向量 空间向量
零 向 量:
单位向量:
相反向量:
相等向量:
共线向量:
一、空间向量的有关概念
解 (2)A为假命题,根据向量相等的定义知,两向量相等,不仅模要相等,而且还要方向相同,而A中向
量a与b的方向不一定相同;
√
解(1)A中,单位向量长度相等,方向不确定;B中,|a|=|b|只能说明a,b的长度相等而方向不确定;
C中,向量不能比较大小.
一、空间向量的有关概念
C为真命题,向量的相等满足传递性;D为假命题,平行向量不一定具有传递性,当b=0时,a与c不
一定平行.
√
√
【练1】如图所示,以长方体ABCD-A1B1C1D1的八个顶点的两点为起点和终点的向量中,
一、空间向量的有关概念
二、空间向量的线性运算及其运算律
运算:空间向量的加法、减法、数乘向量的定义与平面向量的运算一样
运算律:⑴加法交换律:
⑵加法结合律:
⑶数乘分配律:
二、空间向量的线性运算及其运算律
几点注意 :
⑵首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量.即:
⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
⑶两个向量相加的平行四边形法则在空间仍然成立.
二、空间向量的线性运算及其运算律
√
例2 (多选)如图,在正方体ABCD -A1B1C1D1中,下列各式运算结果为 的是( )
√
二、空间向量的线性运算及其运算律
0
解 方法一(转化为加法运算)
方法二(转化为减法运算)
二、空间向量的线性运算及其运算律
解(1)∵P是C1D1的中点,
二、空间向量的线性运算及其运算律
解(2)∵N是BC的中点,
二、空间向量的线性运算及其运算律
解(3)∵M是AA1的中点,
二、空间向量的线性运算及其运算律
《二》利用数乘运算进行向量表示的技巧
二、空间向量的线性运算及其运算律
(1)用反向量:向量的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.
(2)用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,
必要时可采用空间向量的自由平移获得运算结果.
【悟】 《一》空间向量加法、减法运算的两个技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量
转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
二、空间向量的线性运算及其运算律
【练2】如图,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,
请化简以下式子,并在图中标出化简结果.
二、空间向量的线性运算及其运算律
【练3】已知四边形ABCD为正方形,P是四边形ABCD所在平面外一点,P在平面ABCD上
的射影恰好是正方形的中心O,Q是CD的中点,求下列各题中x,y的值.
∴x=2,y=-2.
三、共线定理、共面定理及其应用
共线向量
【规定】:零向量与任意向量共线.
三、共线定理、共面定理及其应用
共线定理
O
A
B
P
a
O
A
B
P
a
我们知道,任意两个空间向量总是共面的,但三个空间向量
既可能是共面的,也可能是不共面的。
O
A
l
三、共线定理、共面定理及其应用
共面向量
那么,什么情况下三个空间向量共面呢?
三、共线定理、共面定理及其应用
共面定理
O
A
C
B
三、共线定理、共面定理及其应用
共面定理
O
A
C
B
α
三、共线定理、共面定理及其应用
共面定理
O
A
B
C
D
E
F
G
H
三、共线定理、共面定理及其应用
1、空间向量的概念
课堂小结
2、空间向量的运算
3 、共线向量(平行向量)的概念及空间向量共线的充要条件
4、共面向量的概念及向量共面的充要条件
作业:
课本P5-6 练习1,2,3,4,5
本课结束
“
”
