人教A版2019选择性必修第一册1.1.2 空间向量的数量积运算 课件(共33张ppt)
文档属性
| 名称 | 人教A版2019选择性必修第一册1.1.2 空间向量的数量积运算 课件(共33张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 15:49:12 | ||
图片预览









文档简介
(共33张PPT)
1.1.2 空间向量的数量积运算
第 1 章空间向量与立体几何
人教A版2019选修第一册
01空间两个向量夹角
目录
02空间两个向量数量积
03空间向量数量积的性质
04投影向量
05空间向量数量积满足的运算律
1.掌握空间向量的数量积,空间向量的夹角
2.掌握空间向量数量积的性质及运算律
3.能利用空间向量的数量积判断两个向量的
垂直及平行
学习目标
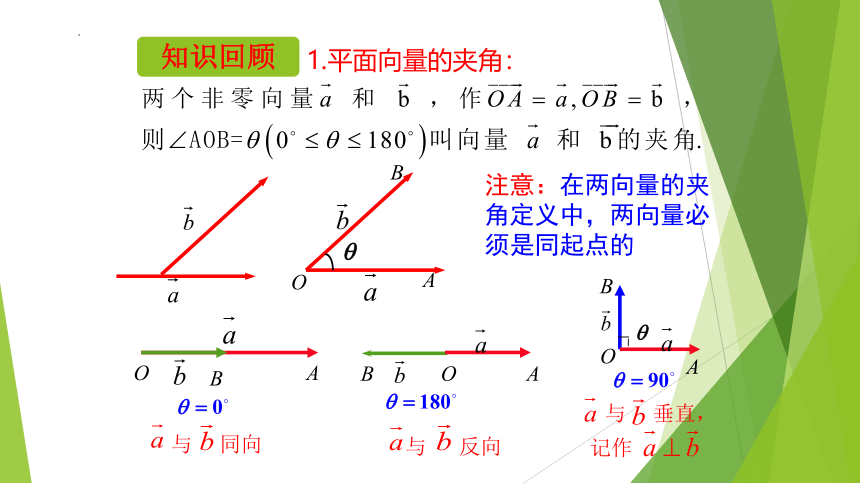
与 反向
O
A
B
O
A
与 同向
O
A
B
B
记作
与 垂直,
O
A
B
注意:在两向量的夹角定义中,两向量必须是同起点的
1.平面向量的夹角:
知识回顾
平面向量的数量积的定义:
2.平面向量的数量积
求两个向量的数量积需先确定这两个向量的模和夹角,
当夹角和长度不确定时,可用已知夹角和长度的向量来表示该向量,
再代入计算.
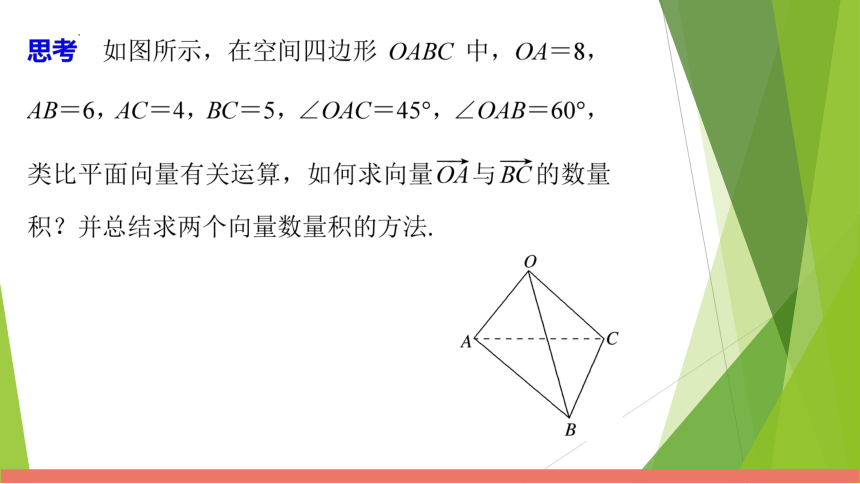
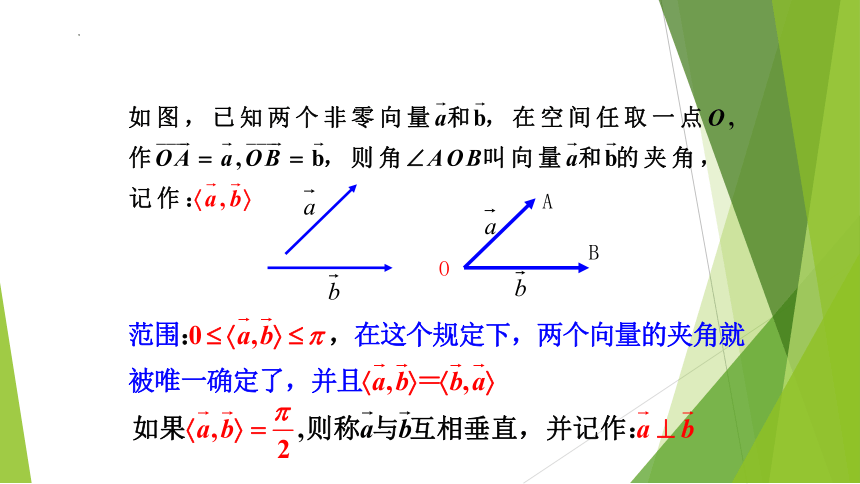
1.空间两个向量夹角
O
A
B
2.空间两个向量的数量积
注意:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
3.空间向量的数量积性质
对于非零向量 ,有:
4. 投影向量
思考:在平面向量的学习中,我们学习了向量的投影。类似地,向量 在向量 上的投影有什么意义?向量 向向量 的投影呢?向量 向向量 的投影呢?
图1.1-11
5.空间向量的数量积满足
的运算律
注意:
数量积不满足结合律
典例解析
典例1
典例2
课堂基础练习
A
B
A1
C1
B1
C
1.如图,在正三棱柱ABC-A1B1C1 中,若AB= BB1,则AB1与BC1所成角的大小为( )
A. B. C. D.
B
2.已知a、b是异面直线,且a⊥b,e1、e2分别为取自直线a、b上的单位向量,且a=2e1+3e2,b=ke1-4e2,a⊥b,则实数k的值为___.
解析 由a⊥b,得a·b=0,
∴(2e1+3e2)·(ke1-4e2)=0,
∴2k-12=0,∴k=6.
6
3.已知在平行六面体ABCD-A'B'C'D'中, AB=4, AD=3,AA'=5,
∠BAD=90°,∠BAA'=∠DAA'=60°, 求对角线AC'的长。
D'
C'
B'
D
A
B
C
A'
D'
C'
B'
D
A
B
C
A'
课堂提升练习
1.BB1⊥平面ABC,且△ABC是∠B=90°的等腰直角三角形,
ABB1A1、 BB1C1C的对角线都分别相互垂直且相等,若AB=a,
求异面直线BA1与AC所成的角.
因为AB⊥BC,BB1⊥AB,BB1⊥BC,
(1)定义:已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b.
(2)数量积的运算律
数乘向量与向量数量积的结合律 (λa)·b=______
交换律 a·b=_____
分配律 a·(b+c)=_________
a·b+a·c
λ(a·b)
b·a
课堂小结
(3)空间向量的夹角
∠AOB
[0,π]
两个向量数量积的性质 ①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b=______;若反向,则a·b=________.
特别地,a·a=____或|a|=
③若θ为a,b的夹角,则cos θ=_______
④|a·b|≤|a|·|b|
空间向量的数量积的性质
a·b=0
|a|·|b|
-|a|·|b|
|a|2
THANKS
“
”
1.1.2 空间向量的数量积运算
第 1 章空间向量与立体几何
人教A版2019选修第一册
01空间两个向量夹角
目录
02空间两个向量数量积
03空间向量数量积的性质
04投影向量
05空间向量数量积满足的运算律
1.掌握空间向量的数量积,空间向量的夹角
2.掌握空间向量数量积的性质及运算律
3.能利用空间向量的数量积判断两个向量的
垂直及平行
学习目标
与 反向
O
A
B
O
A
与 同向
O
A
B
B
记作
与 垂直,
O
A
B
注意:在两向量的夹角定义中,两向量必须是同起点的
1.平面向量的夹角:
知识回顾
平面向量的数量积的定义:
2.平面向量的数量积
求两个向量的数量积需先确定这两个向量的模和夹角,
当夹角和长度不确定时,可用已知夹角和长度的向量来表示该向量,
再代入计算.
1.空间两个向量夹角
O
A
B
2.空间两个向量的数量积
注意:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
3.空间向量的数量积性质
对于非零向量 ,有:
4. 投影向量
思考:在平面向量的学习中,我们学习了向量的投影。类似地,向量 在向量 上的投影有什么意义?向量 向向量 的投影呢?向量 向向量 的投影呢?
图1.1-11
5.空间向量的数量积满足
的运算律
注意:
数量积不满足结合律
典例解析
典例1
典例2
课堂基础练习
A
B
A1
C1
B1
C
1.如图,在正三棱柱ABC-A1B1C1 中,若AB= BB1,则AB1与BC1所成角的大小为( )
A. B. C. D.
B
2.已知a、b是异面直线,且a⊥b,e1、e2分别为取自直线a、b上的单位向量,且a=2e1+3e2,b=ke1-4e2,a⊥b,则实数k的值为___.
解析 由a⊥b,得a·b=0,
∴(2e1+3e2)·(ke1-4e2)=0,
∴2k-12=0,∴k=6.
6
3.已知在平行六面体ABCD-A'B'C'D'中, AB=4, AD=3,AA'=5,
∠BAD=90°,∠BAA'=∠DAA'=60°, 求对角线AC'的长。
D'
C'
B'
D
A
B
C
A'
D'
C'
B'
D
A
B
C
A'
课堂提升练习
1.BB1⊥平面ABC,且△ABC是∠B=90°的等腰直角三角形,
ABB1A1、 BB1C1C的对角线都分别相互垂直且相等,若AB=a,
求异面直线BA1与AC所成的角.
因为AB⊥BC,BB1⊥AB,BB1⊥BC,
(1)定义:已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b.
(2)数量积的运算律
数乘向量与向量数量积的结合律 (λa)·b=______
交换律 a·b=_____
分配律 a·(b+c)=_________
a·b+a·c
λ(a·b)
b·a
课堂小结
(3)空间向量的夹角
∠AOB
[0,π]
两个向量数量积的性质 ①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b=______;若反向,则a·b=________.
特别地,a·a=____或|a|=
③若θ为a,b的夹角,则cos θ=_______
④|a·b|≤|a|·|b|
空间向量的数量积的性质
a·b=0
|a|·|b|
-|a|·|b|
|a|2
THANKS
“
”
