【暑假预习真题汇编】小学数学六年级上册第一单元长方体与正方体易错点检测卷 苏教版(含答案)
文档属性
| 名称 | 【暑假预习真题汇编】小学数学六年级上册第一单元长方体与正方体易错点检测卷 苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 275.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 00:00:00 | ||
图片预览


文档简介
【暑假预习真题汇编】小学数学六年级上册第一单元长方体与正方体易错点检测卷-苏教版
一、选择题
1.(2021·江苏连云港·小升初真题)将下图的纸片折起来可以做成一个正方体。这个正方体2号面的对面是( )号面。
A.3 B.5 C.6
2.(2020·全国·六年级专题练习)用一根长52cm的铁丝,能焊成一个长6cm、宽4cm、高( )cm的长方体。
A.2 B.3 C.4
3.(2022·安徽·蚌埠市淮上区教育体育局教学研究室六年级期末)一个长方体的前面和上面是完全相同的长方形,下面说法中正确的有( )。
①这个长方体有8条棱的长度是相等的
②这个长方体的左右两个面是大小相同的正方形
③这个长方体可能有4个面是正方形
A.①②③ B.①② C.②③
4.(2021·江苏·六年级单元测试)棱长为9dm正方体,切成3个相同的长方体,表面积将会增加( )dm2。
A.81 B.162 C.324 D.648
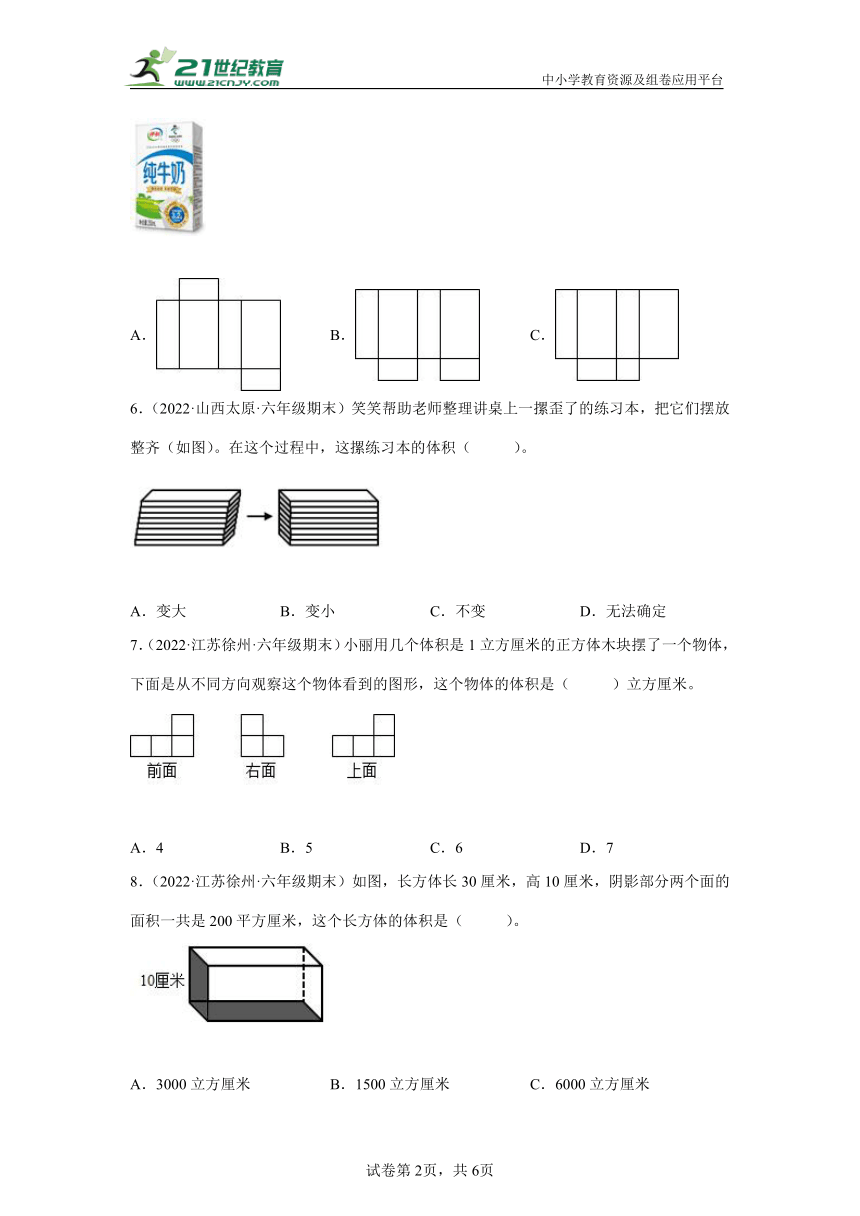
5.(2022·山西·太原市小店区实验小学校六年级期末)将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平。得到的图形可能是( )。
A. B. C.
6.(2022·山西太原·六年级期末)笑笑帮助老师整理讲桌上一摞歪了的练习本,把它们摆放整齐(如图)。在这个过程中,这摞练习本的体积( )。
A.变大 B.变小 C.不变 D.无法确定
7.(2022·江苏徐州·六年级期末)小丽用几个体积是1立方厘米的正方体木块摆了一个物体,下面是从不同方向观察这个物体看到的图形,这个物体的体积是( )立方厘米。
A.4 B.5 C.6 D.7
8.(2022·江苏徐州·六年级期末)如图,长方体长30厘米,高10厘米,阴影部分两个面的面积一共是200平方厘米,这个长方体的体积是( )。
A.3000立方厘米 B.1500立方厘米 C.6000立方厘米
二、图形计算
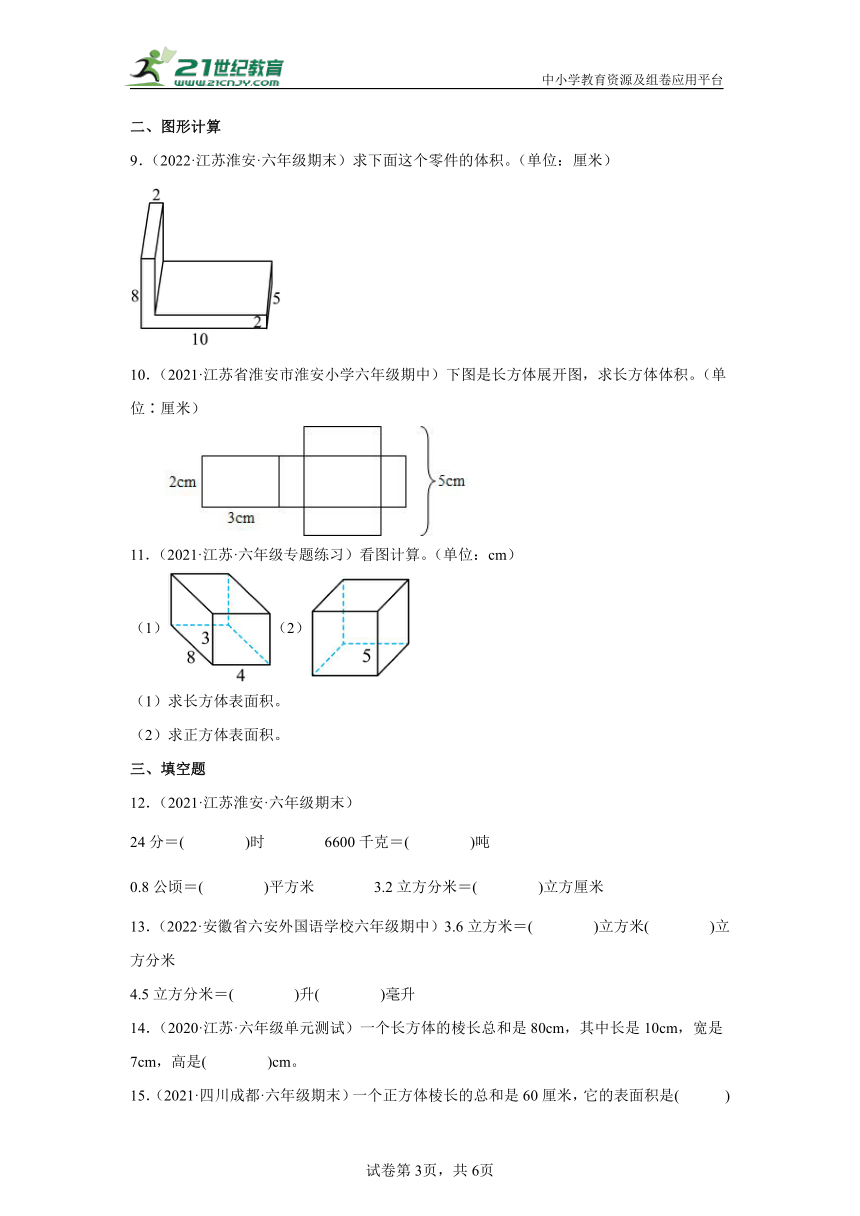
9.(2022·江苏淮安·六年级期末)求下面这个零件的体积。(单位:厘米)
10.(2021·江苏省淮安市淮安小学六年级期中)下图是长方体展开图,求长方体体积。(单位∶厘米)
11.(2021·江苏·六年级专题练习)看图计算。(单位:cm)
(1)(2)
(1)求长方体表面积。
(2)求正方体表面积。
三、填空题
12.(2021·江苏淮安·六年级期末)
24分=( )时 6600千克=( )吨
0.8公顷=( )平方米 3.2立方分米=( )立方厘米
13.(2022·安徽省六安外国语学校六年级期中)3.6立方米=( )立方米( )立方分米
4.5立方分米=( )升( )毫升
14.(2020·江苏·六年级单元测试)一个长方体的棱长总和是80cm,其中长是10cm,宽是7cm,高是( )cm。
15.(2021·四川成都·六年级期末)一个正方体棱长的总和是60厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
16.(2021·江苏无锡·小升初真题)下面是一个长方体的展开图。
(1)如果底面数字是1,那么数字( )在上面。
(2)如果数字3在前面,从右面看是数字5,那么数字( )在上面。
(3)相交于同一个顶点的三个面上的数字之和最大是( )。
17.(2021·江苏南京·小升初真题)棱长是4厘米的正方体的表面积是( )平方厘米,体积是( )立方厘米,可以截成棱长是2厘米的正方体( )个。
18.(2021·福建宁德·六年级期末)一个长方体盒子,从里面量,长7分米,宽6分米,高5分米,如果把棱长2分米的积木装进盒子,并使积木不外露,最多可以装( )块。
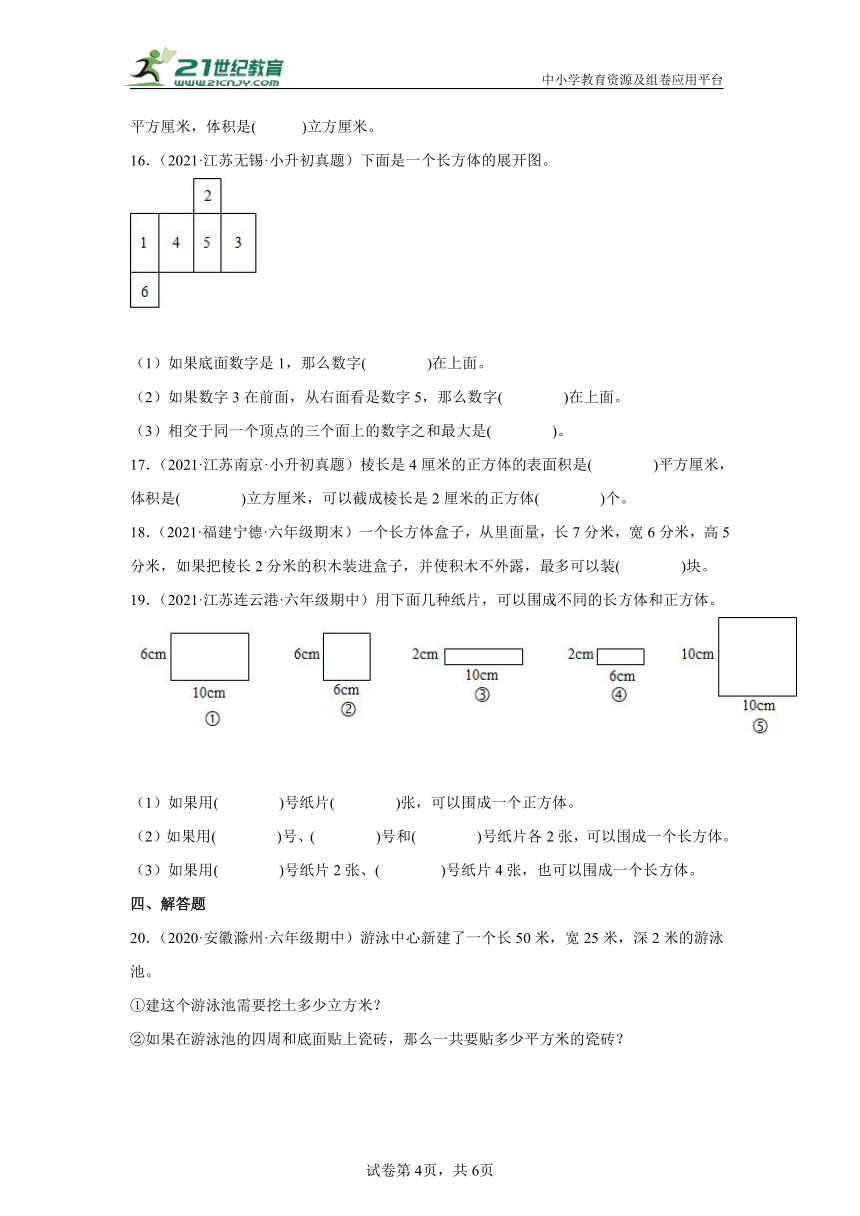
19.(2021·江苏连云港·六年级期中)用下面几种纸片,可以围成不同的长方体和正方体。
(1)如果用( )号纸片( )张,可以围成一个正方体。
(2)如果用( )号、( )号和( )号纸片各2张,可以围成一个长方体。
(3)如果用( )号纸片2张、( )号纸片4张,也可以围成一个长方体。
四、解答题
20.(2020·安徽滁州·六年级期中)游泳中心新建了一个长50米,宽25米,深2米的游泳池。
①建这个游泳池需要挖土多少立方米?
②如果在游泳池的四周和底面贴上瓷砖,那么一共要贴多少平方米的瓷砖?
21.(2019·江苏·六年级单元测试)一个长、宽、高分别为40厘米、30厘米、20厘米的小纸箱,在所有的棱上粘上一圈胶带,至少需要多长的胶带?
22.(2021·江苏省南京市芳草园小学小升初真题)某校将建一个底面是长方形的游泳池,长50米,宽10米,深3米。
(1)这个游泳池的占地面积是多少平方米?
(2)挖这样的一个游泳池,需要挖出多少立方米的土?
(3)在这个游泳池的四壁和底面贴上瓷砖,贴瓷砖的面积是多少平方米?
(4)沿游泳池的内壁1米高处用红漆画一条水位线,水位线全长多少米?
23.(2021·江苏连云港·六年级期中)有一个花坛,高0.4米,底面是边长1.2米的正方形。四周用砖砌成,砖墙的厚度是0.2米,中间填满泥土。
(1)花坛所占的空间有多大?
(2)如果在花坛的侧面贴瓷砖,需要瓷砖多少平方米?
(3)花坛里大约有泥土多少立方米?
24.(2022·山西太原·六年级期末)2021年11月。迎泽大街东延段正式通车。在施工的过程中,一个施工队要在一块长120米,宽30米的长方形路面上铺设0.2米厚的水稳层(水泥沙石的混合体),铺设的水稳层的体积是多少立方米?
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.A
【解析】
【分析】
根据正方体展开图的特征,折叠成正方体后:1号面对应6号面,2号面对应3号面,4号面对应5号面;据此解答即可。
【详解】
将下图的纸片折起来可以做成一个正方体。这个正方体2号面的对面是3号面。
故答案为:A
【点睛】
本题是考查正方体的展开图,培养学生的观察能力和空间想象能力。
2.B
【解析】
【分析】
长方体有12条棱,长、宽、高各4条;根据长方体的棱长总和=(长+宽+高)×4可知,长方体的高=棱长总和÷4-长-宽,代入数据计算即可。
【详解】
52÷4-6-4
=13-6-4
=7-4
=3(cm)
故答案为:B
【点睛】
掌握长方体的特征以及灵活运用长方体的棱长总和计算公式是解题的关键。
3.B
【解析】
【分析】
长方体的特征,长、宽、高 各有4条,相对的面完全相同;根据题意,一个长方体的前面和上面是完全相同的长方形,这个长方体的前后上下四个面相等,由此可知,这个长方体的宽和高相等,有8条棱的长度相等;左右两边是正方形;如果长和宽相等,有6个面是正方形,如果长和宽不相等,只有左右两个面是正方形,据此解答。
【详解】
根据分析可知:
①一个长方体的前面和上面是完全相同的长方形,说明宽和高相等,有8条棱相等,说法正确;
②宽和高相等,这个长方体的左右两个面是大小相同的正方形,说法正确;
③如果长和宽相等,就是一个正方体,6个面相等,如果长和宽不相等,则就是左右两个面是正方形,原题干说法错误。
只用①②说法正确。
故答案选:B
【点睛】
本题考查长方体的特征,根据长方体的特征进行解答。
4.C
【解析】
【分析】
正方体的6个面都是完全相同的正方形;把一个正方体切成3个相同的长方体,需切2刀,切一刀增加2个正方形的面积,切2刀,增加2×2=4个正方形的面积;每个正方形的面积是(9×9)dm2,再乘4,就是增加的表面积。
【详解】
2×2=4(个)
9×9×4
=81×4
=324(dm2)
故答案为:C
【点睛】
掌握切一刀增加2个面,那么切n刀,增加2n个面是解题的关键。
5.A
【解析】
【分析】
根据长方体展开图的特征:“1-4-1”型,“2-3-1”型,“2-2-2”型,“3-3”型,进行解答。
【详解】
A.属于长方体展开图的“1-4-1”型结构,可能数牛奶包装盒的展开图;
B.不属于长方体展开图的特征,不是长方体牛奶包装盒的展开图;
C.不属于长方体展开图的特征,不是长方体牛奶包装盒的展开图。
故答案选:A
【点睛】
本题考查长方体展开图的特征,熟记展开图的特征,进行解答。
6.C
【解析】
【分析】
笑笑帮助老师整理讲桌上一摞歪了的练习本,把它们摆放整齐(如图)。在这个过程中,它的形状发生了变化,但它所占空间的大小不变,所以体积不变,据此选择。
【详解】
笑笑帮助老师整理讲桌上一摞歪了的练习本,把它们摆放整齐(如图)。在这个过程中,这摞练习本的体积不变。
故选择:C
【点睛】
此题考查了对体积的认识,明确物体所占空间的大小是体积。
7.B
【解析】
【分析】
从前面看至少有4个1立方厘米的正方体,结合从上面和右面看到的图形可知,物体后面还有1个1立方厘米的正方体,右齐,一共有5个正方体木块,即这个物体的体积是5立方厘米。
【详解】
1×5=5(立方厘米)
故答案选:B
【点睛】
本题考查根据三视图确定物体个数,要用空间的想象能力,观察要仔细。
8.B
【解析】
【分析】
根据图可知,阴影部分是底面和一个侧面,底面的面积:长×宽,侧面的面积:宽×高,由于两个面的面积一共是200平方厘米,即长×宽+宽×高=200,根据乘法分配律可知,宽×(长+高)=200,由于长是30厘米,高是10厘米,由此即可求出宽是多少厘米,再根据长方体的体积公式:长×宽×高,把数代入公式即可求解。
【详解】
200÷(30+10)
=200÷40
=5(厘米)
30×10×5
=300×5
=1500(立方厘米)
故答案为:B。
【点睛】
本题主要考查长方体的体积公式,要注意清楚的知道长方体每个面的面积表示是用哪两条边相乘。
9.160立方厘米
【解析】
【分析】
这个零件由两个长方体组成,长方体的体积=长×宽×高,据此求出两个长方体的体积,相加即可。
【详解】
10×5×2+(8-2)×5×2
=100+60
=160(立方厘米)
10.9立方厘米
【解析】
【分析】
观察图形可知,长方体的高×1再加上长方体的宽等于5cm,高等于5cm减去2cm再除以2,再根据长方体的体积公式:长×宽×高,代入数据,即可解答。
【详解】
3×2×[(5-2)÷2]
=6×[3÷2]
=6×1.5
=9(立方厘米)
11.(1)136平方厘米;(2)150平方厘米
【解析】
【分析】
长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的表面积=棱长×棱长×6,代入数据计算即可。
【详解】
(1)(8×4+8×3+4×3)×2
=(32+24+12)×2
=68×2
=136(平方厘米);
(2)5×5×6
=25×6
=150(平方厘米)
12. 6.6 8000 3200
【解析】
【分析】
根据1小时=60分钟,1吨=1000千克,1公顷=10000平方米,1立方分米=1000立方厘米,高级单位化成低级单位,乘进率,低级单位化成高级单位,除以进率,据此解答。
【详解】
24分=时
6600千克=6.6吨
0.8公顷=8000平方米
3.2立方分米=3200立方厘米
【点睛】
此题主要考查时间、质量、面积、体积单位之间的换算,注意单位之间的进率。
13. 3 600 4 500
【解析】
【分析】
3.6立方米看作3立方米与0.6立方米之和,把0.6立方米乘进率1000化成600立方分米;
立方分米与升是等量关系二者互化数值不变,4.5升看作4升与0.5升之和,把0.5升乘进率1000化成500毫升。
【详解】
由分析可知;3.6立方米=3立方米600立方分米
4.5立方分米=4升500毫升
【点睛】
此题是考查体积、容积的单位换算.由高级单位化低级单位乘进率,由低级单位化高级单位除以进率。
14.3
【解析】
【分析】
因为“长方体的棱长总和=(长+宽+高)×4”,所以先用“80÷4”求出长方体一条长、宽和高的和,用长、宽、高的和减去长和宽即可求出高。
【详解】
80÷4-10-7
=20-10-7
=3(cm)
【点睛】
此题考查的目的是掌握长方体的特征及棱长总和的计算方法,根据棱长总和的计算方法进行解答。
15. 150 125
【解析】
【分析】
由题意得正方体的棱长=总和÷12,再根据正方体的表面积=6a2计算出表面积,根据计算体积。
【详解】
60÷12=5(厘米)
6×5×5=150(平方厘米)
5×5×5=125(立方厘米)
【点睛】
根据正方体的棱长=总和÷12求出正方体的棱长是解题的关键。
16. 5 6 15
【解析】
【分析】
根据长方体的特点:相对的面完全相同,题干中,1和5相对,2和6相对,3和4相对;相交于同一个顶点的三个面上的数字之和最大则是相邻的三个面4、5、6之和,据此解答。
【详解】
由分析得:
(1)如果底面数字是1,那么数字5在上面。
(2)如果数字3在前面,从右面看是数字5,那么数字6在上面。
(3)相交于同一个顶点的三个面上的数字之和最大是:
4+5+6
=9+6
=15
【点睛】
此题考查的是长方体的展开图的应用,掌握长方体的展开图并能够根据展开图想象拼接是解题关键。
17. 96 64 8
【解析】
【分析】
①根据正方体的表面积和体积公式即可求得其表面积和体积;
②抓住正方体分割前后的体积不变,即可得出小正方体的个数。
【详解】
4×4×6=96(平方厘米)
4×4×4=64(立方厘米)
2×2×2=8(立方厘米)
64÷8=8(个)
则棱长是4厘米的正方体的表面积是96平方厘米,体积是64立方厘米,可以截成棱长是2厘米的正方体8个。
【点睛】
此题考查了正方体表面积和体积公式的灵活应用,以及正方体分割的方法。
18.18
【解析】
【分析】
用除法分别求出长方体的长、宽、高包含几个正方体的棱长,再连乘即可。
【详解】
7÷2=3(个)……1(分米)
6÷2=3(个)
5÷2=2(个)……1(分米)
3×3×2
=9×2
=18(块)
【点睛】
本题考查了长方体体积的实际应用,掌握方法认真解答即可。
19. ② 6 ① ③ ④ ② ①
【解析】
【分析】
根据长方体和正方体的特征,进行解答。
【详解】
(1)如果用②、⑤号纸片各6张,都可以围成一个正方体。(答案不唯一)
(2)如果用①号、③号和④号纸片各2张,可以围成一个长方体。
(3)如果用②号纸片2张、①号纸片4张,也可以围成一个长方形。(答案不唯一)
【点睛】
本题考查长方体、正方体的特征,根据它们的特征进行解答。
20.①2500立方米②1550平方米
【解析】
【分析】
①求挖出的土的体积就是求出长方体游泳池的容积。长方体的容积=长×宽×高,据此解答。
②贴瓷砖的面积包括长方体游泳池的四个侧面和一个底面。根据长方体的表面积公式,贴瓷砖的面积=长×宽+(长×高+宽×高)×2,据此代入数据计算。
【详解】
①50×25×2=2500(立方米)
答:建这个游泳池需要挖土2500立方米。
②50×25+(50×2+25×2)×2
=1250+150×2
=1250+300
=1550(平方米)
答:一共要贴1550平方米的瓷砖。
【点睛】
本题考查长方体表面积和容积的应用。掌握并熟练运用长方体的表面积和体积公式是解题的关键。
21.360厘米
【解析】
【分析】
由题意可知,求胶带的长度即是求出长方体的总棱长,根据长方体的总棱长=(长+宽+高)×4,据此代入数值进行计算即可。
【详解】
(40+30+20)×4
=90×4
=360(厘米)
答:至少需要360厘米的胶带。
【点睛】
本题考查长方体的总棱长,明确长方体的总棱长=(长+宽+高)×4是解题的关键。
22.(1)500平方米;(2)1500立方米;(3)860平方米;(4)120米
【解析】
【分析】
(1)占地面积与游泳池的深度无关,根据长方形的面积公式“S=ab”即可算出。
(2)挖出土的体积就是这个长方体游泳池的体积,根据长方体体积公式“V=abh”即可求出。
(3)要在四壁和池底贴上瓷砖,只求它的5个面的总面积,根据长方体的表面积的计算方法解答。
(4)沿着游泳池的内壁1米高处画水位线,即游泳池的底面周长,根据长方形周长公式计算即可。
【详解】
(1)50×10=500(平方米)
答:这个游泳池的占地面积是500平方米。
(2)50×10×3
=500×3
=1500(立方米)
答:挖这样的一个游泳池,需要挖出1500立方米的土。
(3)50×10+50×3×2+10×3×2
=500+300+60
=860(平方米)
答:在这个游泳池的四壁和底面贴上瓷砖,贴瓷砖的面积是860平方米。
(4)50×2+10×2
=100+20
=120(米)
答:沿游泳池的内壁1米高处用红漆画一条水位线,水位线全长120米。
【点睛】
此题主要是考查长方体体积、表面积的计算,关键是记住计算公式;注意,这个游泳池的占地面积与游泳池的深度无关。
23.(1)0.576立方米
(2)1.92平方米
(3)0.256立方米
【解析】
【分析】
(1)求花坛所占空间,就是求这个长1.2米,宽1.2米,高是0.4米的长方体的体积,根据长方体的体积公式:长×宽×高,代入数据,求出所占空间;
(2)求需要瓷砖多少平方米,就是求这个长方体的侧面积,这四个面相等,用长方体的长×高×4,代入数据,求出侧面积;
(3)求花坛里大约有泥土多少立方米,求这个长方体的容积,由于是用0.2米的砖砌成,用长方体的长减去0.2×2,求出花坛里面的边长,再根据长方体体积公式,求出容积。
【详解】
(1)1.2×1.2×0.4
=1.44×0.4
=0.576(立方米)
答:花坛所占空间有0.576立方米。
(2)1.2×0.4×4
=0.48×4
=1.92(平方米)
答:需要瓷砖1.92平方米。
(3)(1.2-0.2×2)×(1.2-0.2×2)×0.4
=0.8×0.8×0.4
=0.64×0.4
=0.256(立方米)
答:花坛里大约有泥土0.256立方米。
【点睛】
本题考查长方体体积(容积)公式的应用,以及求长方体侧面积;关键明确求长方体的花坛容积,长方体的长、宽分别要减去两个0.2米。
24.720立方米
【解析】
【分析】
水稳层的体积=长×宽×水稳层的厚度,代入数据计算即可。
【详解】
120×30×0.2
=3600×0.2
=720(立方米)
答:铺设的水稳层的体积是720立方米。
【点睛】
此题考查了长方体的体积计算,需牢记公式并能灵活运用。
答案第1页,共2页
答案第12页,共12页
一、选择题
1.(2021·江苏连云港·小升初真题)将下图的纸片折起来可以做成一个正方体。这个正方体2号面的对面是( )号面。
A.3 B.5 C.6
2.(2020·全国·六年级专题练习)用一根长52cm的铁丝,能焊成一个长6cm、宽4cm、高( )cm的长方体。
A.2 B.3 C.4
3.(2022·安徽·蚌埠市淮上区教育体育局教学研究室六年级期末)一个长方体的前面和上面是完全相同的长方形,下面说法中正确的有( )。
①这个长方体有8条棱的长度是相等的
②这个长方体的左右两个面是大小相同的正方形
③这个长方体可能有4个面是正方形
A.①②③ B.①② C.②③
4.(2021·江苏·六年级单元测试)棱长为9dm正方体,切成3个相同的长方体,表面积将会增加( )dm2。
A.81 B.162 C.324 D.648
5.(2022·山西·太原市小店区实验小学校六年级期末)将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平。得到的图形可能是( )。
A. B. C.
6.(2022·山西太原·六年级期末)笑笑帮助老师整理讲桌上一摞歪了的练习本,把它们摆放整齐(如图)。在这个过程中,这摞练习本的体积( )。
A.变大 B.变小 C.不变 D.无法确定
7.(2022·江苏徐州·六年级期末)小丽用几个体积是1立方厘米的正方体木块摆了一个物体,下面是从不同方向观察这个物体看到的图形,这个物体的体积是( )立方厘米。
A.4 B.5 C.6 D.7
8.(2022·江苏徐州·六年级期末)如图,长方体长30厘米,高10厘米,阴影部分两个面的面积一共是200平方厘米,这个长方体的体积是( )。
A.3000立方厘米 B.1500立方厘米 C.6000立方厘米
二、图形计算
9.(2022·江苏淮安·六年级期末)求下面这个零件的体积。(单位:厘米)
10.(2021·江苏省淮安市淮安小学六年级期中)下图是长方体展开图,求长方体体积。(单位∶厘米)
11.(2021·江苏·六年级专题练习)看图计算。(单位:cm)
(1)(2)
(1)求长方体表面积。
(2)求正方体表面积。
三、填空题
12.(2021·江苏淮安·六年级期末)
24分=( )时 6600千克=( )吨
0.8公顷=( )平方米 3.2立方分米=( )立方厘米
13.(2022·安徽省六安外国语学校六年级期中)3.6立方米=( )立方米( )立方分米
4.5立方分米=( )升( )毫升
14.(2020·江苏·六年级单元测试)一个长方体的棱长总和是80cm,其中长是10cm,宽是7cm,高是( )cm。
15.(2021·四川成都·六年级期末)一个正方体棱长的总和是60厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
16.(2021·江苏无锡·小升初真题)下面是一个长方体的展开图。
(1)如果底面数字是1,那么数字( )在上面。
(2)如果数字3在前面,从右面看是数字5,那么数字( )在上面。
(3)相交于同一个顶点的三个面上的数字之和最大是( )。
17.(2021·江苏南京·小升初真题)棱长是4厘米的正方体的表面积是( )平方厘米,体积是( )立方厘米,可以截成棱长是2厘米的正方体( )个。
18.(2021·福建宁德·六年级期末)一个长方体盒子,从里面量,长7分米,宽6分米,高5分米,如果把棱长2分米的积木装进盒子,并使积木不外露,最多可以装( )块。
19.(2021·江苏连云港·六年级期中)用下面几种纸片,可以围成不同的长方体和正方体。
(1)如果用( )号纸片( )张,可以围成一个正方体。
(2)如果用( )号、( )号和( )号纸片各2张,可以围成一个长方体。
(3)如果用( )号纸片2张、( )号纸片4张,也可以围成一个长方体。
四、解答题
20.(2020·安徽滁州·六年级期中)游泳中心新建了一个长50米,宽25米,深2米的游泳池。
①建这个游泳池需要挖土多少立方米?
②如果在游泳池的四周和底面贴上瓷砖,那么一共要贴多少平方米的瓷砖?
21.(2019·江苏·六年级单元测试)一个长、宽、高分别为40厘米、30厘米、20厘米的小纸箱,在所有的棱上粘上一圈胶带,至少需要多长的胶带?
22.(2021·江苏省南京市芳草园小学小升初真题)某校将建一个底面是长方形的游泳池,长50米,宽10米,深3米。
(1)这个游泳池的占地面积是多少平方米?
(2)挖这样的一个游泳池,需要挖出多少立方米的土?
(3)在这个游泳池的四壁和底面贴上瓷砖,贴瓷砖的面积是多少平方米?
(4)沿游泳池的内壁1米高处用红漆画一条水位线,水位线全长多少米?
23.(2021·江苏连云港·六年级期中)有一个花坛,高0.4米,底面是边长1.2米的正方形。四周用砖砌成,砖墙的厚度是0.2米,中间填满泥土。
(1)花坛所占的空间有多大?
(2)如果在花坛的侧面贴瓷砖,需要瓷砖多少平方米?
(3)花坛里大约有泥土多少立方米?
24.(2022·山西太原·六年级期末)2021年11月。迎泽大街东延段正式通车。在施工的过程中,一个施工队要在一块长120米,宽30米的长方形路面上铺设0.2米厚的水稳层(水泥沙石的混合体),铺设的水稳层的体积是多少立方米?
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.A
【解析】
【分析】
根据正方体展开图的特征,折叠成正方体后:1号面对应6号面,2号面对应3号面,4号面对应5号面;据此解答即可。
【详解】
将下图的纸片折起来可以做成一个正方体。这个正方体2号面的对面是3号面。
故答案为:A
【点睛】
本题是考查正方体的展开图,培养学生的观察能力和空间想象能力。
2.B
【解析】
【分析】
长方体有12条棱,长、宽、高各4条;根据长方体的棱长总和=(长+宽+高)×4可知,长方体的高=棱长总和÷4-长-宽,代入数据计算即可。
【详解】
52÷4-6-4
=13-6-4
=7-4
=3(cm)
故答案为:B
【点睛】
掌握长方体的特征以及灵活运用长方体的棱长总和计算公式是解题的关键。
3.B
【解析】
【分析】
长方体的特征,长、宽、高 各有4条,相对的面完全相同;根据题意,一个长方体的前面和上面是完全相同的长方形,这个长方体的前后上下四个面相等,由此可知,这个长方体的宽和高相等,有8条棱的长度相等;左右两边是正方形;如果长和宽相等,有6个面是正方形,如果长和宽不相等,只有左右两个面是正方形,据此解答。
【详解】
根据分析可知:
①一个长方体的前面和上面是完全相同的长方形,说明宽和高相等,有8条棱相等,说法正确;
②宽和高相等,这个长方体的左右两个面是大小相同的正方形,说法正确;
③如果长和宽相等,就是一个正方体,6个面相等,如果长和宽不相等,则就是左右两个面是正方形,原题干说法错误。
只用①②说法正确。
故答案选:B
【点睛】
本题考查长方体的特征,根据长方体的特征进行解答。
4.C
【解析】
【分析】
正方体的6个面都是完全相同的正方形;把一个正方体切成3个相同的长方体,需切2刀,切一刀增加2个正方形的面积,切2刀,增加2×2=4个正方形的面积;每个正方形的面积是(9×9)dm2,再乘4,就是增加的表面积。
【详解】
2×2=4(个)
9×9×4
=81×4
=324(dm2)
故答案为:C
【点睛】
掌握切一刀增加2个面,那么切n刀,增加2n个面是解题的关键。
5.A
【解析】
【分析】
根据长方体展开图的特征:“1-4-1”型,“2-3-1”型,“2-2-2”型,“3-3”型,进行解答。
【详解】
A.属于长方体展开图的“1-4-1”型结构,可能数牛奶包装盒的展开图;
B.不属于长方体展开图的特征,不是长方体牛奶包装盒的展开图;
C.不属于长方体展开图的特征,不是长方体牛奶包装盒的展开图。
故答案选:A
【点睛】
本题考查长方体展开图的特征,熟记展开图的特征,进行解答。
6.C
【解析】
【分析】
笑笑帮助老师整理讲桌上一摞歪了的练习本,把它们摆放整齐(如图)。在这个过程中,它的形状发生了变化,但它所占空间的大小不变,所以体积不变,据此选择。
【详解】
笑笑帮助老师整理讲桌上一摞歪了的练习本,把它们摆放整齐(如图)。在这个过程中,这摞练习本的体积不变。
故选择:C
【点睛】
此题考查了对体积的认识,明确物体所占空间的大小是体积。
7.B
【解析】
【分析】
从前面看至少有4个1立方厘米的正方体,结合从上面和右面看到的图形可知,物体后面还有1个1立方厘米的正方体,右齐,一共有5个正方体木块,即这个物体的体积是5立方厘米。
【详解】
1×5=5(立方厘米)
故答案选:B
【点睛】
本题考查根据三视图确定物体个数,要用空间的想象能力,观察要仔细。
8.B
【解析】
【分析】
根据图可知,阴影部分是底面和一个侧面,底面的面积:长×宽,侧面的面积:宽×高,由于两个面的面积一共是200平方厘米,即长×宽+宽×高=200,根据乘法分配律可知,宽×(长+高)=200,由于长是30厘米,高是10厘米,由此即可求出宽是多少厘米,再根据长方体的体积公式:长×宽×高,把数代入公式即可求解。
【详解】
200÷(30+10)
=200÷40
=5(厘米)
30×10×5
=300×5
=1500(立方厘米)
故答案为:B。
【点睛】
本题主要考查长方体的体积公式,要注意清楚的知道长方体每个面的面积表示是用哪两条边相乘。
9.160立方厘米
【解析】
【分析】
这个零件由两个长方体组成,长方体的体积=长×宽×高,据此求出两个长方体的体积,相加即可。
【详解】
10×5×2+(8-2)×5×2
=100+60
=160(立方厘米)
10.9立方厘米
【解析】
【分析】
观察图形可知,长方体的高×1再加上长方体的宽等于5cm,高等于5cm减去2cm再除以2,再根据长方体的体积公式:长×宽×高,代入数据,即可解答。
【详解】
3×2×[(5-2)÷2]
=6×[3÷2]
=6×1.5
=9(立方厘米)
11.(1)136平方厘米;(2)150平方厘米
【解析】
【分析】
长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的表面积=棱长×棱长×6,代入数据计算即可。
【详解】
(1)(8×4+8×3+4×3)×2
=(32+24+12)×2
=68×2
=136(平方厘米);
(2)5×5×6
=25×6
=150(平方厘米)
12. 6.6 8000 3200
【解析】
【分析】
根据1小时=60分钟,1吨=1000千克,1公顷=10000平方米,1立方分米=1000立方厘米,高级单位化成低级单位,乘进率,低级单位化成高级单位,除以进率,据此解答。
【详解】
24分=时
6600千克=6.6吨
0.8公顷=8000平方米
3.2立方分米=3200立方厘米
【点睛】
此题主要考查时间、质量、面积、体积单位之间的换算,注意单位之间的进率。
13. 3 600 4 500
【解析】
【分析】
3.6立方米看作3立方米与0.6立方米之和,把0.6立方米乘进率1000化成600立方分米;
立方分米与升是等量关系二者互化数值不变,4.5升看作4升与0.5升之和,把0.5升乘进率1000化成500毫升。
【详解】
由分析可知;3.6立方米=3立方米600立方分米
4.5立方分米=4升500毫升
【点睛】
此题是考查体积、容积的单位换算.由高级单位化低级单位乘进率,由低级单位化高级单位除以进率。
14.3
【解析】
【分析】
因为“长方体的棱长总和=(长+宽+高)×4”,所以先用“80÷4”求出长方体一条长、宽和高的和,用长、宽、高的和减去长和宽即可求出高。
【详解】
80÷4-10-7
=20-10-7
=3(cm)
【点睛】
此题考查的目的是掌握长方体的特征及棱长总和的计算方法,根据棱长总和的计算方法进行解答。
15. 150 125
【解析】
【分析】
由题意得正方体的棱长=总和÷12,再根据正方体的表面积=6a2计算出表面积,根据计算体积。
【详解】
60÷12=5(厘米)
6×5×5=150(平方厘米)
5×5×5=125(立方厘米)
【点睛】
根据正方体的棱长=总和÷12求出正方体的棱长是解题的关键。
16. 5 6 15
【解析】
【分析】
根据长方体的特点:相对的面完全相同,题干中,1和5相对,2和6相对,3和4相对;相交于同一个顶点的三个面上的数字之和最大则是相邻的三个面4、5、6之和,据此解答。
【详解】
由分析得:
(1)如果底面数字是1,那么数字5在上面。
(2)如果数字3在前面,从右面看是数字5,那么数字6在上面。
(3)相交于同一个顶点的三个面上的数字之和最大是:
4+5+6
=9+6
=15
【点睛】
此题考查的是长方体的展开图的应用,掌握长方体的展开图并能够根据展开图想象拼接是解题关键。
17. 96 64 8
【解析】
【分析】
①根据正方体的表面积和体积公式即可求得其表面积和体积;
②抓住正方体分割前后的体积不变,即可得出小正方体的个数。
【详解】
4×4×6=96(平方厘米)
4×4×4=64(立方厘米)
2×2×2=8(立方厘米)
64÷8=8(个)
则棱长是4厘米的正方体的表面积是96平方厘米,体积是64立方厘米,可以截成棱长是2厘米的正方体8个。
【点睛】
此题考查了正方体表面积和体积公式的灵活应用,以及正方体分割的方法。
18.18
【解析】
【分析】
用除法分别求出长方体的长、宽、高包含几个正方体的棱长,再连乘即可。
【详解】
7÷2=3(个)……1(分米)
6÷2=3(个)
5÷2=2(个)……1(分米)
3×3×2
=9×2
=18(块)
【点睛】
本题考查了长方体体积的实际应用,掌握方法认真解答即可。
19. ② 6 ① ③ ④ ② ①
【解析】
【分析】
根据长方体和正方体的特征,进行解答。
【详解】
(1)如果用②、⑤号纸片各6张,都可以围成一个正方体。(答案不唯一)
(2)如果用①号、③号和④号纸片各2张,可以围成一个长方体。
(3)如果用②号纸片2张、①号纸片4张,也可以围成一个长方形。(答案不唯一)
【点睛】
本题考查长方体、正方体的特征,根据它们的特征进行解答。
20.①2500立方米②1550平方米
【解析】
【分析】
①求挖出的土的体积就是求出长方体游泳池的容积。长方体的容积=长×宽×高,据此解答。
②贴瓷砖的面积包括长方体游泳池的四个侧面和一个底面。根据长方体的表面积公式,贴瓷砖的面积=长×宽+(长×高+宽×高)×2,据此代入数据计算。
【详解】
①50×25×2=2500(立方米)
答:建这个游泳池需要挖土2500立方米。
②50×25+(50×2+25×2)×2
=1250+150×2
=1250+300
=1550(平方米)
答:一共要贴1550平方米的瓷砖。
【点睛】
本题考查长方体表面积和容积的应用。掌握并熟练运用长方体的表面积和体积公式是解题的关键。
21.360厘米
【解析】
【分析】
由题意可知,求胶带的长度即是求出长方体的总棱长,根据长方体的总棱长=(长+宽+高)×4,据此代入数值进行计算即可。
【详解】
(40+30+20)×4
=90×4
=360(厘米)
答:至少需要360厘米的胶带。
【点睛】
本题考查长方体的总棱长,明确长方体的总棱长=(长+宽+高)×4是解题的关键。
22.(1)500平方米;(2)1500立方米;(3)860平方米;(4)120米
【解析】
【分析】
(1)占地面积与游泳池的深度无关,根据长方形的面积公式“S=ab”即可算出。
(2)挖出土的体积就是这个长方体游泳池的体积,根据长方体体积公式“V=abh”即可求出。
(3)要在四壁和池底贴上瓷砖,只求它的5个面的总面积,根据长方体的表面积的计算方法解答。
(4)沿着游泳池的内壁1米高处画水位线,即游泳池的底面周长,根据长方形周长公式计算即可。
【详解】
(1)50×10=500(平方米)
答:这个游泳池的占地面积是500平方米。
(2)50×10×3
=500×3
=1500(立方米)
答:挖这样的一个游泳池,需要挖出1500立方米的土。
(3)50×10+50×3×2+10×3×2
=500+300+60
=860(平方米)
答:在这个游泳池的四壁和底面贴上瓷砖,贴瓷砖的面积是860平方米。
(4)50×2+10×2
=100+20
=120(米)
答:沿游泳池的内壁1米高处用红漆画一条水位线,水位线全长120米。
【点睛】
此题主要是考查长方体体积、表面积的计算,关键是记住计算公式;注意,这个游泳池的占地面积与游泳池的深度无关。
23.(1)0.576立方米
(2)1.92平方米
(3)0.256立方米
【解析】
【分析】
(1)求花坛所占空间,就是求这个长1.2米,宽1.2米,高是0.4米的长方体的体积,根据长方体的体积公式:长×宽×高,代入数据,求出所占空间;
(2)求需要瓷砖多少平方米,就是求这个长方体的侧面积,这四个面相等,用长方体的长×高×4,代入数据,求出侧面积;
(3)求花坛里大约有泥土多少立方米,求这个长方体的容积,由于是用0.2米的砖砌成,用长方体的长减去0.2×2,求出花坛里面的边长,再根据长方体体积公式,求出容积。
【详解】
(1)1.2×1.2×0.4
=1.44×0.4
=0.576(立方米)
答:花坛所占空间有0.576立方米。
(2)1.2×0.4×4
=0.48×4
=1.92(平方米)
答:需要瓷砖1.92平方米。
(3)(1.2-0.2×2)×(1.2-0.2×2)×0.4
=0.8×0.8×0.4
=0.64×0.4
=0.256(立方米)
答:花坛里大约有泥土0.256立方米。
【点睛】
本题考查长方体体积(容积)公式的应用,以及求长方体侧面积;关键明确求长方体的花坛容积,长方体的长、宽分别要减去两个0.2米。
24.720立方米
【解析】
【分析】
水稳层的体积=长×宽×水稳层的厚度,代入数据计算即可。
【详解】
120×30×0.2
=3600×0.2
=720(立方米)
答:铺设的水稳层的体积是720立方米。
【点睛】
此题考查了长方体的体积计算,需牢记公式并能灵活运用。
答案第1页,共2页
答案第12页,共12页
