【暑假衔接真题汇编】小学数学六年级上册第七单元扇形统计图重难点检测卷-人教版(含解析)
文档属性
| 名称 | 【暑假衔接真题汇编】小学数学六年级上册第七单元扇形统计图重难点检测卷-人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 770.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 00:00:00 | ||
图片预览




文档简介
【暑假衔接真题汇编】小学六年级上册第七单元扇形统计图重难点检测卷-人教版
一、选择题
1.(2020·广西玉林·六年级期末)要反映某市今年各类谷物产量占粮食总产量的百分比,应绘制( )统计图。
A.条形 B.扇形 C.折线
2.(2021·山东济南·六年级期末)既能看出两组数据的变化趋势,又能对两组数据的差异进行分析,这是( )统计图的优势。
A.单式折线 B.复式折线 C.复式条形 D.扇形
3.(2021·浙江宁波·六年级期末)野象群一路北上,引起民众的极大关注,为普及象群知识,需要绘制统计图。下面各话题,更适合用折线统计图表示的是( ),更适合用扇形统计图表示的是( )。
①几头成年野象睡眠时间长短比较
②野象在亚洲地区分布的百分比
③三十年来野象数量增减变化情况
④幼年和成年野象一天食量多少情况
A.①和③ B.①和④ C.③和② D.②和④
4.(2022·广东阳江·六年级期末)如图,一个圆形花坛内种了三种花用条形统计图表示各种花的占地面积正确的是( )。
A. B. C.
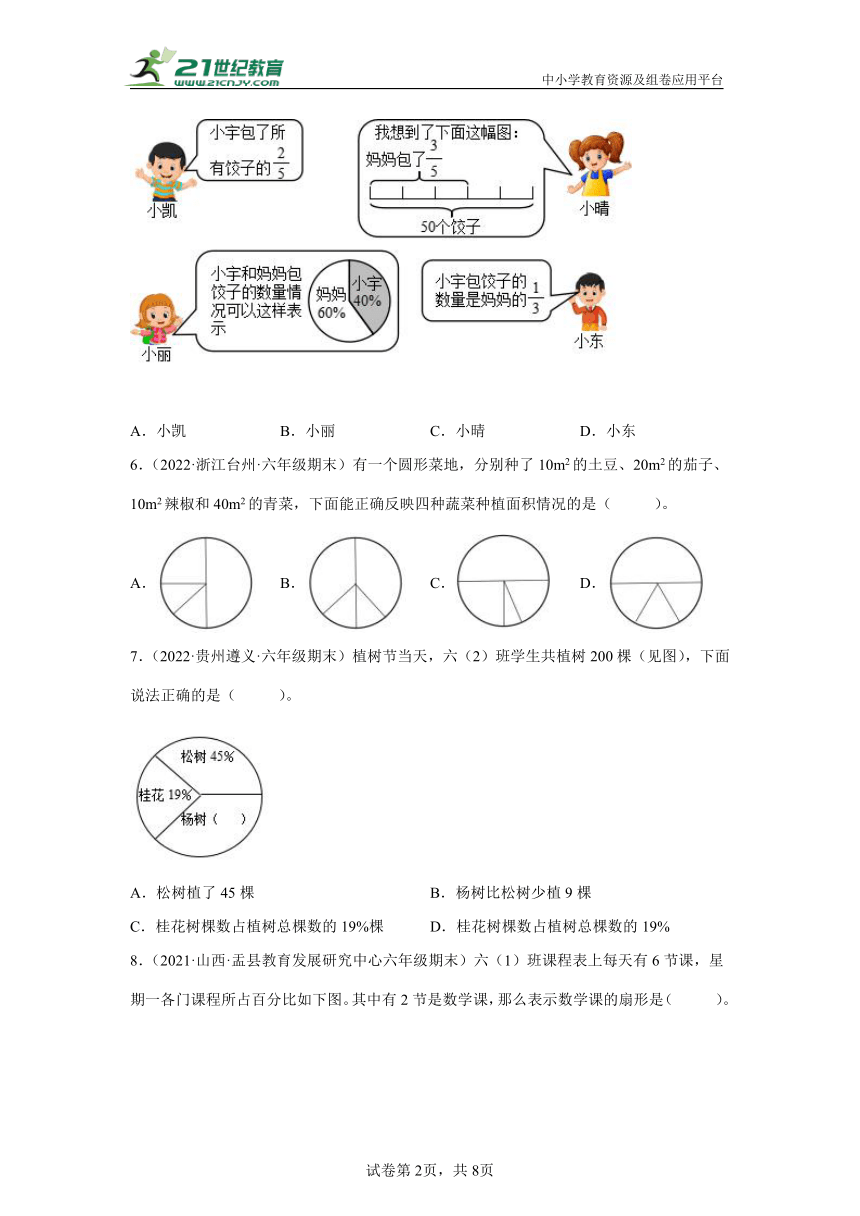
5.(2021·福建厦门·六年级期末)放假期间,小宇一家在包饺子,爸爸负责擀饺子皮,他们一共包了50个饺子,其中妈妈包了30个。根据信息四人中联想错误的是( )。
A.小凯 B.小丽 C.小晴 D.小东
6.(2022·浙江台州·六年级期末)有一个圆形菜地,分别种了10m2的土豆、20m2的茄子、10m2辣椒和40m2的青菜,下面能正确反映四种蔬菜种植面积情况的是( )。
A. B. C. D.
7.(2022·贵州遵义·六年级期末)植树节当天,六(2)班学生共植树200棵(见图),下面说法正确的是( )。
A.松树植了45棵 B.杨树比松树少植9棵
C.桂花树棵数占植树总棵数的19%棵 D.桂花树棵数占植树总棵数的19%
8.(2021·山西·盂县教育发展研究中心六年级期末)六(1)班课程表上每天有6节课,星期一各门课程所占百分比如下图。其中有2节是数学课,那么表示数学课的扇形是( )。
A.甲 B.乙 C.丙
二、填空题
9.(2019·山西阳泉·六年级期中)某小学校德育处对全校500名同学进行了“看电视”情况的问卷调查,得到信息如下表,并制作了一幅扇形统计图。
基本不看电视 13%
偶尔看电视 35%
经常看电视 52%
(1)在这幅统计图中标记①、②、③的区域分别对应着( )、( )、( )这三部分人数。
(2)根据信息,可以算出“基本不看电视”的有( )人,“偶尔看电视”的有( )人,“经常看电视”的有( )人。
10.(2022·江苏宿迁·六年级期中)观察扇形统计图。
如果圆代表整体,那么扇形( )表示整体的45%;
如果用这个圆代表9公顷的稻田,那么扇形A代表( )公顷;
如果用整个圆代表菜地的总面积,则C代表的面积比A代表的面积多( )%;
如果用整个圆代表红星小学的全体学生的人数,已知B代表的人数比A代表的人数多60人,则红星小学共有( )人。
11.(2022·全国·六年级专题练习)下图为六(2)班同学喜欢各类书籍的扇形调查统计图。
喜欢学习指导书的同学有9人。则喜欢科技书的有( )人,图中括号内应填写( )。
12.(2020·安徽铜陵·六年级期末)如图是某校图书馆三种书册数统计图,根据统计图完成统计表。
种类 故事书 连环画 科技书
百分率
册数 900
13.(2021·四川内江·六年级期末)观察下边的扇形统计图,回答下列问题:
(1)如果用这个圆代表总体,________表示总体的;
(2)如果用整个圆代表12公顷稻田,占________公顷;
(3)如果用整个圆代表全校学生人数,比多150人,全校________人。
三、判断题
14.(2022·全国·六年级专题练习)要反映微山县去年空气质量为优的天数与全年天数的关系,绘制扇形统计图较合适。( )
15.(2020·重庆市永川区教育科学研究所六年级期末)要想清楚地看出优优家2019年7月至12月天然气用量的增减变化情况,最好选用扇形统计图。( )
16.(2021·广西·贺州市平桂区教育科学研究所六年级期末)条形统计图能清楚的表示出数量的多少,折线统计图更容易看出数量增减变化的情况,扇形统计图可以看出各部分与整体的关系。( )
17.(2022·全国·六年级专题练习)要反映学校运动会参加踢毽、跳绳、足球、乒乓球等项目的人数占总人数的百分比,选用扇形统计图比较合适。( )
18.(2021·甘肃武威·小升初真题)股市通常用折线统计图反映某些数据的变化情况。( )
四、解答题
19.(2021·江西·上犹县教学研究室六年级期末)小慧对本校六年级学生最喜欢的文艺节目情况进行了调查,并绘制了下面统计图,根据图中信息回答:
(1)喜欢相声节目的人数占百分之几?
(2)小慧所在学校六年级一共有多少人?
(3)喜欢杂技节目的有多少人?
20.(2022·贵州·遵义市播州区泮水镇第一小学六年级期末)2021年教育部办公厅印发了《关于加强中小学生手机管理工作的通知》,倡导做好手机管理工作,保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏。下图是阳光小学六年级200名学生使用手机情况统计图,请观察统计图并回答问题。
(1)手机用于查资料的有( )人。
(2)本次调查活动中,手机用于电话通讯的人数占调查总人数的,手机用于玩游戏的人数占调查总人数的( )%。
(3)根据以上调查结果,你想对学生们提出什么意见?
21.(2022·四川乐山·六年级期末)为了丰富课后服务的活动内容,某校准备开设民乐社团。为了了解学生的喜好情况,学校对部分学生进行了调查,并制作了两个不完整的统计图,请完成以下问题。
(1)这次调查的人数一共有( )人。
(2)请把条形统计图和扇形统计图补充完整。
(3)如果学校有1500人,参加古筝社团有多少人?
22.(2021·山东青岛·六年级期末)对六(1)班同学进行最喜欢的运动项目调查(每人只选1项),结果绘制成以下两幅不完整的统计图。人
(1)将条形统计图补充完整。
(2)六(1)班一共有( )名学生。喜欢跑步的人数占全班总人数的( )%。
23.(2022·广东阳江·六年级期末)幸福小区实行垃圾分类,物业管理员统计了一个星期中居民垃圾分类的情况,统计如图。
(1)如图,该小区产生( )最多,占( ),另外,有害垃圾占( )。
(2)这个星期该小区共产生了42吨垃圾,其中可回收垃圾有多少吨?
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共8页
参考答案:
1.B
【解析】
【分析】
条形统计图可以直观地看出数量的多少;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况;扇形统计图能清楚地看出各部分数量与总数量之间的关系。据此解答。
【详解】
根据各统计图的特点,要反映某市今年各类谷物产量占粮食总产量的百分比,应绘制扇形统计图。
故答案为:B
【点睛】
本题考查统计图的选择。掌握各统计图的特点是解题的关键。
2.B
【解析】
【分析】
条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图:可以清楚地看出各部分数量与总数量之间,部分与部分之间的关系;据此解答。
【详解】
分析可知,表示数据的变化趋势应选择折线统计图,因为有两组数据,所以既能看出两组数据的变化趋势,又能对两组数据的差异进行分析,这时选择复式折线统计图比较合适。
故答案为:B
【点睛】
理解并掌握折线统计图、条形统计图、扇形统计图的特点及作用是解答题目的关键。
3.C
【解析】
【分析】
折线统计图能清楚地反映事物的变化情况;扇形统计图能清楚地表示出各部分在总体中所占的百分比;根据统计图的特点来判断,即可求解。
【详解】
③中三十年来野象数量增减变化情况反映的是数量增减变化情况,因此更适合用折线统计图;
②中野象在亚洲地区分布的百分比表示的是各部分在总体中所占的百分比,因此应选用扇形统计图。
故答案为:C
【点睛】
本题主要考查根据统计图的特点来选择统计图。
4.C
【解析】
【分析】
把这个花坛的总面积看作单位“1”,其中迎春花占,菊花和月季各占,据此对照三幅条形统计图进行选择即可。
【详解】
首先排除图和图B,因为这两幅图中表示菊花和月季的直条长度不相等,不符合题意。
只有图C能够表示三者花的占地面积关系。
故答案为:C
【点睛】
此题考查的目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
5.D
【解析】
【分析】
由题意可知,爸爸负责擀饺子皮,小宇和妈妈包饺子,他们一共包了50个饺子,其中妈妈包了30个。所以小宇包了50-30=20(个),进一步验证小凯、小晴、小丽、小东的想法。
【详解】
小凯: ,小凯的想法是正确的;
小晴:30÷50=,小晴想法正确。
小丽:30÷50×100%=60%,,小丽的想法正确。
小东:,小东的想法是错误的。
故答案为:D
【点睛】
本题考查扇形统计图、分数与除法的关系以及含百分数的运算,属于综合题,逐项进行分析即可。
6.A
【解析】
【分析】
先求出四种蔬菜的面积比10∶20∶10∶40,化简为1∶2∶1∶4,也是它们圆心角的度数比;再根据一个圆是360°除以总份数(1+2+1+4),求出一份数,最后分别乘各蔬菜的份数,求出每种蔬菜的圆心角度数;结合扇形统计图,进行选择。
【详解】
10∶20∶10∶40=1∶2∶1∶4
360°÷(1+2+1+4)
=360°÷8
=45°
土豆:45°×1=45°
茄子:45°×2=90°
辣椒:45°×1=45°
青菜:45°×4=180°
A.扇形统计图的圆心角有180°、90°、2个45°,符合题意;
B.扇形统计图的圆心角没有180°、90°,不符合题意;
C.扇形统计图的圆心角没有2个45°,不符合题意;
D.扇形统计图的圆心角没有90°,不符合题意。
故答案为:A
【点睛】
掌握扇形统计图的特点、比的意义及应用,能够根据提供的信息选择正确的扇形统计图。
7.D
【解析】
【分析】
把六(2)班学生植树总棵数看作单位“1”,用减法求出杨树棵数占植树总棵数的百分率,再根据求一个数的百分之几是多少的计算方法,求出松树和杨树的植树棵数;百分数只表示两个数之间的倍比关系,不能带单位名称,据此解答。
【详解】
A.200×45%=90(棵)
所以,松树植了90棵。
B.杨树:200×(1-45%-19%)
=200×0.36
=72(棵)
90-72=18(棵)
所以,杨树比松树少植18棵。
C.由百分数的意义可知,桂花树棵数占植树总棵数的19%,百分数后面不能带单位名称。
D.由扇形统计图可知,桂花树棵数占植树总棵数的19%。
故答案为:D
【点睛】
掌握百分数的意义,并且能够根据扇形统计图提供的信息解决有关实际问题是解答题目的关键。
8.C
【解析】
【分析】
用除法表示数学课占课程总数的分率,数学课的扇形所对圆心角=360°×数学课占课程总数的分率,据此解答。
【详解】
360°×=120°
故答案为:C
【点睛】
求出数学课占课程总数的分率,并根据求一个数的几分之几是多少的计算方法求出扇形圆心角的度数是解答题目的关键。
9.(1) 经常看电视 偶尔看电视 基本不看电视
(2) 65 175 260
【解析】
【分析】
由图可知,这是一副扇形统计图,可以体现部分占整体的百分比,经常看电视的有52%,
占总人数最多,所以①是经常看电视的。偶尔看电视的有35%,所以②是偶尔看电视的。
基本不看电视的有13%,占总人数最少,所以③是基本不看电视的。
(2)学校德育处是对全校500名同学进行了“看电视”情况的问卷调查。根据信息,可以推算出“基本不看电视”的有500×13%=65(人),“偶尔看电视”的有500×35%=175(人),“经常看电视”的有500×52%=260(人)。
(1)
在这幅统计图中标记①、②、③的区域分别对应着经常看电视、偶尔看电视、基本不看电视这三部分人数。
(2)
500×13%=65(人)
500×35%=175(人)
500×52%=260(人)
【点睛】
此题主要考查从统计图和统计表中获取数据进行解答计算的能力。
10. C 2.25 20 1200
【解析】
【分析】
根据题意,把圆看做单位“1”,A表示圆的90°÷360°×100%=25%,所以扇形C表示圆的1-25%-30%=45%;
把稻田的总面积看成单位“1”,先求出A占总数的百分之几,然后用乘法求出A表示的面积;
用C占总数的百分之几减去A占总数的百分之几即可解答;
把全校的总人数看成单位“1”,先求出扇形B比扇形A多的百分之几,多的百分数之几所对应的数量是60人,由此用除法求出总人数。
【详解】
90°÷360°×100%
=0.25×100%
=25%
1-25%-30%
=75%-30%
=45%
25%×9=2.25(公顷)
45%-25%=20%
30%-25%=5%
60÷5%=1200(人)
【点睛】
本题考查了扇形统计图的特点,整个圆表示总量单位“1”,每个扇形表示表示总量的百分之几(或几分之几)。
11. 17 42%
【解析】
【分析】
用喜欢学习指导书的人数除以占总数的百分率求出总人数。根据百分数乘法的意义,用总人数乘喜欢科技书占总人数的百分率即可求出喜欢科技书的人数。用1减去喜欢三类书的百分率即可求出喜欢文艺书占的百分率,也就是括号里应填的数。
【详解】
9÷18%=50(人)
50×34%=17(人)
1-6%-18%-34%
=94%-18%-34%
=76%-34%
=42%
【点睛】
本题考查如何从扇形统计图中获取有效信息,并根据获取的信息解决实际问题。
12.见详解
【解析】
【分析】
观察扇形统计图,把总册数看成单位“1”,已知连环画占,故事书占,剩下的是科技书;而表格中只知道科技书的本数,所以要求总册数以及故事书、连环画书的本数,需要知道科技书占总册数的百分之几,即,再用900册除以这个分率即可求出总册数;然后用总册数乘就是故事书的册数,用总册数乘就是连环画书的册数。
【详解】
1-25%-30%
=75%-30%
=45%
(册)
(册)
(册)
表格如下:
种类 故事书 连环画 科技书
百分率
册数 600 500 900
【点睛】
此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可。
13.(1)C
(2)3
(3)1000
【解析】
【分析】
(1)把总体看作单位“1”,通过观察扇形统计图可知:B占30%,A占所占的百分比小于B,而C所占的百分比大于B,所以C表示总体的45%;
(2)把12公顷看作单位“1”,已知B占30%,C占45%,那么A占(1-30%-45%),根据一个数乘百分数的意义,用乘法解答;
(3)把全校学生人数看作单位“1”,已知B占30%,C占45%,那么C比B多150人占全校学生人数的(45%-30%),根据已知一个数的百分之几是多少,求这个数,用除法解答。
(1)
C表示总体的45%;
(2)
12×(1-30%-45%)
=12×25%
=12×0.25
=3(公顷)
(3)
150÷(45%-30%)
=150÷15%
=150÷0.15
=1000(人)
【点睛】
此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据扇形统计图提供的信息,解决有关的实际问题。
14.√
【解析】
【分析】
通过扇形统计图可以很清楚地表示出各部分数量与总数之间的关系。
【详解】
扇形统计图能清楚地表示部分数量与总数间关系,所以要反映微山县去年空气质量为优的天数与全年天数的关系,绘制扇形统计图较合适。
故答案为:√
【点睛】
此题应根据扇形统计图各自的特点进行解答。
15.×
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】
由分析得:要想清楚地看出优优家2019年7月至12月天然气用量的增减变化情况,最好选用折线统计图。
故答案为:×
【点睛】
此题考查的是选择合适的统计图,掌握统计图的特点是解题关键。
16.√
【解析】
【分析】
根据条形统计图、折线统计图、扇形统计图的特征分析题中说法是否正确即可。
【详解】
条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图:扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系;
由上可知,题中说法正确。
故答案为:√
【点睛】
理解并掌握各统计图的特征是解答题目的关键。
17.√
【解析】
【分析】
条形统计图很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况判断即可。
【详解】
要反映学校运动会参加踢毽、跳绳、足球、乒乓球等项目的人数占总人数的百分比,选用扇形统计图比较合适。
故答案为:√
【点睛】
此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行判断。
18.√
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】
根据统计图的特点可知:
股市通常用折线统计图反映某些数据的变化情况;说法正确。
故答案为:√。
【点睛】
此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
19.统计图见详解
(1)10%
(2)200人
(3)30人
【解析】
【分析】
(1)把六年级学生最喜欢的文艺节目数量看作单位“1”,用1减去小品、歌曲、杂技和其他所占的百分比即可解答;
(2)根据已知一个数的百分之几是多少,求这个数,根据除法的意义,用除法即可求出六年级的总人数;
(3)根据求一个数的百分之几是多少,用乘法即可求出喜欢杂技节目的人数。
【详解】
(1)1-15%-15%-35%-25%
=85%-15%-35%-25%
=70%-35%-25%
=35%-25%
=10%
答:喜欢相声节目的人数占10%。
(2)70÷35%=200(人)
答:小慧所在学校六年级一共有200人。
(3)200×15%=30(人)
答:喜欢杂技节目的有30人。
【点睛】
本题考查求一个数的百分之几是多少,明确用乘法是解题的关键。
20.(1)45;
(2);25;
(3)见详解(答案不唯一)
【解析】
【分析】
(1)用总人数减去用于电话通讯、玩游戏和其他的人数即可解答。
(2)用电话通讯的人数除以调查总人数即可;用玩游戏的人数除以调查总人数再乘100%即可。
(3)根据统计图提出合理的建议即可。
【详解】
(1)200-75-50-30
=125-50-30
=75-30
=45(人)
(2)75÷200=
50÷200×100%
=0.25×100%
=25%
所以手机用于电话通讯的人数占调查总人数的,手机用于玩游戏的人数占调查总人数的25%。
(3)希望同学少玩一些游戏,多用于学习方面。
【点睛】
本题考查统计图表的综合应用。
21.(1)200人;(2)见详解;(3)375人
【解析】
【分析】
(1)把调查总人数看作单位“1”,用其他社团的人数除以其占总人数的百分率,求出总人数;
(2)根据二胡社团、古琴社团的人数及总人数,求出其占总体的百分率;根据古筝和琵琶社团占总人数的百分率和总人数,求参加古筝和琵琶社团的人数。完成统计图。
(3)根据总人数乘参加古筝社团的百分率,求参加古筝社团的人数。
【详解】
(1)(人
答:这次调查的人数一共有200人。
(2)(人
(人
统计图如下:
(3)(人
答:参加古筝社团的有375人。
【点睛】
本题主要考查统计图表的填充,关键是利用条形统计图和扇形统计图,找到解决问题的条件,计算并完成问题。
22.(1)见解析(2)40;20
【解析】
【分析】
(1)由条形统计图可知:最喜欢乒乓球的有12人,由扇形统计图可知最喜欢乒乓球的人数占总人数的30%,用12除以30%,即可求出总人数;用总人数乘上20%,即可求出最喜欢篮球的人数;用总人数乘上12.5%即可求出最喜欢跳绳的人数;然后完成条形统计图即可;
(2)最喜欢乒乓球的有12人,由扇形统计图可知最喜欢乒乓球的人数占总人数的30%,用12除以30%即可求出总人数;用喜欢踢毽子的人数除以总人数即可。
【详解】
(1)12÷30%=40(人)
40×20%=8(人)
40×12.5%=5(人)
条形统计图如下:
(2)12÷30%=40(人)
8÷40×100%
=0.2×100%
=20%
【点睛】
本题主要考查统计图表的填充,关键利用所给数据完成统计图并回答简单的问题。
23.(1)可回收垃圾;56;4
(2)23.52吨
【解析】
【分析】
(1)通过观察统计图可知,该小区产生的可回收垃圾最多,占,有害垃圾站;
(2)把小区共产生的垃圾总数看作单位“1”,根据求一个数的百分之几是多少,用乘法解答。
【详解】
(1)该小区产生的可回收垃圾最多,占,有害垃圾站。
(2)(吨
答:可回收垃圾有23.52吨。
【点睛】
此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,再根据一个数乘百分数的意义解决问题。
答案第1页,共2页
答案第15页,共17页
一、选择题
1.(2020·广西玉林·六年级期末)要反映某市今年各类谷物产量占粮食总产量的百分比,应绘制( )统计图。
A.条形 B.扇形 C.折线
2.(2021·山东济南·六年级期末)既能看出两组数据的变化趋势,又能对两组数据的差异进行分析,这是( )统计图的优势。
A.单式折线 B.复式折线 C.复式条形 D.扇形
3.(2021·浙江宁波·六年级期末)野象群一路北上,引起民众的极大关注,为普及象群知识,需要绘制统计图。下面各话题,更适合用折线统计图表示的是( ),更适合用扇形统计图表示的是( )。
①几头成年野象睡眠时间长短比较
②野象在亚洲地区分布的百分比
③三十年来野象数量增减变化情况
④幼年和成年野象一天食量多少情况
A.①和③ B.①和④ C.③和② D.②和④
4.(2022·广东阳江·六年级期末)如图,一个圆形花坛内种了三种花用条形统计图表示各种花的占地面积正确的是( )。
A. B. C.
5.(2021·福建厦门·六年级期末)放假期间,小宇一家在包饺子,爸爸负责擀饺子皮,他们一共包了50个饺子,其中妈妈包了30个。根据信息四人中联想错误的是( )。
A.小凯 B.小丽 C.小晴 D.小东
6.(2022·浙江台州·六年级期末)有一个圆形菜地,分别种了10m2的土豆、20m2的茄子、10m2辣椒和40m2的青菜,下面能正确反映四种蔬菜种植面积情况的是( )。
A. B. C. D.
7.(2022·贵州遵义·六年级期末)植树节当天,六(2)班学生共植树200棵(见图),下面说法正确的是( )。
A.松树植了45棵 B.杨树比松树少植9棵
C.桂花树棵数占植树总棵数的19%棵 D.桂花树棵数占植树总棵数的19%
8.(2021·山西·盂县教育发展研究中心六年级期末)六(1)班课程表上每天有6节课,星期一各门课程所占百分比如下图。其中有2节是数学课,那么表示数学课的扇形是( )。
A.甲 B.乙 C.丙
二、填空题
9.(2019·山西阳泉·六年级期中)某小学校德育处对全校500名同学进行了“看电视”情况的问卷调查,得到信息如下表,并制作了一幅扇形统计图。
基本不看电视 13%
偶尔看电视 35%
经常看电视 52%
(1)在这幅统计图中标记①、②、③的区域分别对应着( )、( )、( )这三部分人数。
(2)根据信息,可以算出“基本不看电视”的有( )人,“偶尔看电视”的有( )人,“经常看电视”的有( )人。
10.(2022·江苏宿迁·六年级期中)观察扇形统计图。
如果圆代表整体,那么扇形( )表示整体的45%;
如果用这个圆代表9公顷的稻田,那么扇形A代表( )公顷;
如果用整个圆代表菜地的总面积,则C代表的面积比A代表的面积多( )%;
如果用整个圆代表红星小学的全体学生的人数,已知B代表的人数比A代表的人数多60人,则红星小学共有( )人。
11.(2022·全国·六年级专题练习)下图为六(2)班同学喜欢各类书籍的扇形调查统计图。
喜欢学习指导书的同学有9人。则喜欢科技书的有( )人,图中括号内应填写( )。
12.(2020·安徽铜陵·六年级期末)如图是某校图书馆三种书册数统计图,根据统计图完成统计表。
种类 故事书 连环画 科技书
百分率
册数 900
13.(2021·四川内江·六年级期末)观察下边的扇形统计图,回答下列问题:
(1)如果用这个圆代表总体,________表示总体的;
(2)如果用整个圆代表12公顷稻田,占________公顷;
(3)如果用整个圆代表全校学生人数,比多150人,全校________人。
三、判断题
14.(2022·全国·六年级专题练习)要反映微山县去年空气质量为优的天数与全年天数的关系,绘制扇形统计图较合适。( )
15.(2020·重庆市永川区教育科学研究所六年级期末)要想清楚地看出优优家2019年7月至12月天然气用量的增减变化情况,最好选用扇形统计图。( )
16.(2021·广西·贺州市平桂区教育科学研究所六年级期末)条形统计图能清楚的表示出数量的多少,折线统计图更容易看出数量增减变化的情况,扇形统计图可以看出各部分与整体的关系。( )
17.(2022·全国·六年级专题练习)要反映学校运动会参加踢毽、跳绳、足球、乒乓球等项目的人数占总人数的百分比,选用扇形统计图比较合适。( )
18.(2021·甘肃武威·小升初真题)股市通常用折线统计图反映某些数据的变化情况。( )
四、解答题
19.(2021·江西·上犹县教学研究室六年级期末)小慧对本校六年级学生最喜欢的文艺节目情况进行了调查,并绘制了下面统计图,根据图中信息回答:
(1)喜欢相声节目的人数占百分之几?
(2)小慧所在学校六年级一共有多少人?
(3)喜欢杂技节目的有多少人?
20.(2022·贵州·遵义市播州区泮水镇第一小学六年级期末)2021年教育部办公厅印发了《关于加强中小学生手机管理工作的通知》,倡导做好手机管理工作,保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏。下图是阳光小学六年级200名学生使用手机情况统计图,请观察统计图并回答问题。
(1)手机用于查资料的有( )人。
(2)本次调查活动中,手机用于电话通讯的人数占调查总人数的,手机用于玩游戏的人数占调查总人数的( )%。
(3)根据以上调查结果,你想对学生们提出什么意见?
21.(2022·四川乐山·六年级期末)为了丰富课后服务的活动内容,某校准备开设民乐社团。为了了解学生的喜好情况,学校对部分学生进行了调查,并制作了两个不完整的统计图,请完成以下问题。
(1)这次调查的人数一共有( )人。
(2)请把条形统计图和扇形统计图补充完整。
(3)如果学校有1500人,参加古筝社团有多少人?
22.(2021·山东青岛·六年级期末)对六(1)班同学进行最喜欢的运动项目调查(每人只选1项),结果绘制成以下两幅不完整的统计图。人
(1)将条形统计图补充完整。
(2)六(1)班一共有( )名学生。喜欢跑步的人数占全班总人数的( )%。
23.(2022·广东阳江·六年级期末)幸福小区实行垃圾分类,物业管理员统计了一个星期中居民垃圾分类的情况,统计如图。
(1)如图,该小区产生( )最多,占( ),另外,有害垃圾占( )。
(2)这个星期该小区共产生了42吨垃圾,其中可回收垃圾有多少吨?
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共8页
参考答案:
1.B
【解析】
【分析】
条形统计图可以直观地看出数量的多少;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况;扇形统计图能清楚地看出各部分数量与总数量之间的关系。据此解答。
【详解】
根据各统计图的特点,要反映某市今年各类谷物产量占粮食总产量的百分比,应绘制扇形统计图。
故答案为:B
【点睛】
本题考查统计图的选择。掌握各统计图的特点是解题的关键。
2.B
【解析】
【分析】
条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图:可以清楚地看出各部分数量与总数量之间,部分与部分之间的关系;据此解答。
【详解】
分析可知,表示数据的变化趋势应选择折线统计图,因为有两组数据,所以既能看出两组数据的变化趋势,又能对两组数据的差异进行分析,这时选择复式折线统计图比较合适。
故答案为:B
【点睛】
理解并掌握折线统计图、条形统计图、扇形统计图的特点及作用是解答题目的关键。
3.C
【解析】
【分析】
折线统计图能清楚地反映事物的变化情况;扇形统计图能清楚地表示出各部分在总体中所占的百分比;根据统计图的特点来判断,即可求解。
【详解】
③中三十年来野象数量增减变化情况反映的是数量增减变化情况,因此更适合用折线统计图;
②中野象在亚洲地区分布的百分比表示的是各部分在总体中所占的百分比,因此应选用扇形统计图。
故答案为:C
【点睛】
本题主要考查根据统计图的特点来选择统计图。
4.C
【解析】
【分析】
把这个花坛的总面积看作单位“1”,其中迎春花占,菊花和月季各占,据此对照三幅条形统计图进行选择即可。
【详解】
首先排除图和图B,因为这两幅图中表示菊花和月季的直条长度不相等,不符合题意。
只有图C能够表示三者花的占地面积关系。
故答案为:C
【点睛】
此题考查的目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
5.D
【解析】
【分析】
由题意可知,爸爸负责擀饺子皮,小宇和妈妈包饺子,他们一共包了50个饺子,其中妈妈包了30个。所以小宇包了50-30=20(个),进一步验证小凯、小晴、小丽、小东的想法。
【详解】
小凯: ,小凯的想法是正确的;
小晴:30÷50=,小晴想法正确。
小丽:30÷50×100%=60%,,小丽的想法正确。
小东:,小东的想法是错误的。
故答案为:D
【点睛】
本题考查扇形统计图、分数与除法的关系以及含百分数的运算,属于综合题,逐项进行分析即可。
6.A
【解析】
【分析】
先求出四种蔬菜的面积比10∶20∶10∶40,化简为1∶2∶1∶4,也是它们圆心角的度数比;再根据一个圆是360°除以总份数(1+2+1+4),求出一份数,最后分别乘各蔬菜的份数,求出每种蔬菜的圆心角度数;结合扇形统计图,进行选择。
【详解】
10∶20∶10∶40=1∶2∶1∶4
360°÷(1+2+1+4)
=360°÷8
=45°
土豆:45°×1=45°
茄子:45°×2=90°
辣椒:45°×1=45°
青菜:45°×4=180°
A.扇形统计图的圆心角有180°、90°、2个45°,符合题意;
B.扇形统计图的圆心角没有180°、90°,不符合题意;
C.扇形统计图的圆心角没有2个45°,不符合题意;
D.扇形统计图的圆心角没有90°,不符合题意。
故答案为:A
【点睛】
掌握扇形统计图的特点、比的意义及应用,能够根据提供的信息选择正确的扇形统计图。
7.D
【解析】
【分析】
把六(2)班学生植树总棵数看作单位“1”,用减法求出杨树棵数占植树总棵数的百分率,再根据求一个数的百分之几是多少的计算方法,求出松树和杨树的植树棵数;百分数只表示两个数之间的倍比关系,不能带单位名称,据此解答。
【详解】
A.200×45%=90(棵)
所以,松树植了90棵。
B.杨树:200×(1-45%-19%)
=200×0.36
=72(棵)
90-72=18(棵)
所以,杨树比松树少植18棵。
C.由百分数的意义可知,桂花树棵数占植树总棵数的19%,百分数后面不能带单位名称。
D.由扇形统计图可知,桂花树棵数占植树总棵数的19%。
故答案为:D
【点睛】
掌握百分数的意义,并且能够根据扇形统计图提供的信息解决有关实际问题是解答题目的关键。
8.C
【解析】
【分析】
用除法表示数学课占课程总数的分率,数学课的扇形所对圆心角=360°×数学课占课程总数的分率,据此解答。
【详解】
360°×=120°
故答案为:C
【点睛】
求出数学课占课程总数的分率,并根据求一个数的几分之几是多少的计算方法求出扇形圆心角的度数是解答题目的关键。
9.(1) 经常看电视 偶尔看电视 基本不看电视
(2) 65 175 260
【解析】
【分析】
由图可知,这是一副扇形统计图,可以体现部分占整体的百分比,经常看电视的有52%,
占总人数最多,所以①是经常看电视的。偶尔看电视的有35%,所以②是偶尔看电视的。
基本不看电视的有13%,占总人数最少,所以③是基本不看电视的。
(2)学校德育处是对全校500名同学进行了“看电视”情况的问卷调查。根据信息,可以推算出“基本不看电视”的有500×13%=65(人),“偶尔看电视”的有500×35%=175(人),“经常看电视”的有500×52%=260(人)。
(1)
在这幅统计图中标记①、②、③的区域分别对应着经常看电视、偶尔看电视、基本不看电视这三部分人数。
(2)
500×13%=65(人)
500×35%=175(人)
500×52%=260(人)
【点睛】
此题主要考查从统计图和统计表中获取数据进行解答计算的能力。
10. C 2.25 20 1200
【解析】
【分析】
根据题意,把圆看做单位“1”,A表示圆的90°÷360°×100%=25%,所以扇形C表示圆的1-25%-30%=45%;
把稻田的总面积看成单位“1”,先求出A占总数的百分之几,然后用乘法求出A表示的面积;
用C占总数的百分之几减去A占总数的百分之几即可解答;
把全校的总人数看成单位“1”,先求出扇形B比扇形A多的百分之几,多的百分数之几所对应的数量是60人,由此用除法求出总人数。
【详解】
90°÷360°×100%
=0.25×100%
=25%
1-25%-30%
=75%-30%
=45%
25%×9=2.25(公顷)
45%-25%=20%
30%-25%=5%
60÷5%=1200(人)
【点睛】
本题考查了扇形统计图的特点,整个圆表示总量单位“1”,每个扇形表示表示总量的百分之几(或几分之几)。
11. 17 42%
【解析】
【分析】
用喜欢学习指导书的人数除以占总数的百分率求出总人数。根据百分数乘法的意义,用总人数乘喜欢科技书占总人数的百分率即可求出喜欢科技书的人数。用1减去喜欢三类书的百分率即可求出喜欢文艺书占的百分率,也就是括号里应填的数。
【详解】
9÷18%=50(人)
50×34%=17(人)
1-6%-18%-34%
=94%-18%-34%
=76%-34%
=42%
【点睛】
本题考查如何从扇形统计图中获取有效信息,并根据获取的信息解决实际问题。
12.见详解
【解析】
【分析】
观察扇形统计图,把总册数看成单位“1”,已知连环画占,故事书占,剩下的是科技书;而表格中只知道科技书的本数,所以要求总册数以及故事书、连环画书的本数,需要知道科技书占总册数的百分之几,即,再用900册除以这个分率即可求出总册数;然后用总册数乘就是故事书的册数,用总册数乘就是连环画书的册数。
【详解】
1-25%-30%
=75%-30%
=45%
(册)
(册)
(册)
表格如下:
种类 故事书 连环画 科技书
百分率
册数 600 500 900
【点睛】
此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可。
13.(1)C
(2)3
(3)1000
【解析】
【分析】
(1)把总体看作单位“1”,通过观察扇形统计图可知:B占30%,A占所占的百分比小于B,而C所占的百分比大于B,所以C表示总体的45%;
(2)把12公顷看作单位“1”,已知B占30%,C占45%,那么A占(1-30%-45%),根据一个数乘百分数的意义,用乘法解答;
(3)把全校学生人数看作单位“1”,已知B占30%,C占45%,那么C比B多150人占全校学生人数的(45%-30%),根据已知一个数的百分之几是多少,求这个数,用除法解答。
(1)
C表示总体的45%;
(2)
12×(1-30%-45%)
=12×25%
=12×0.25
=3(公顷)
(3)
150÷(45%-30%)
=150÷15%
=150÷0.15
=1000(人)
【点睛】
此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据扇形统计图提供的信息,解决有关的实际问题。
14.√
【解析】
【分析】
通过扇形统计图可以很清楚地表示出各部分数量与总数之间的关系。
【详解】
扇形统计图能清楚地表示部分数量与总数间关系,所以要反映微山县去年空气质量为优的天数与全年天数的关系,绘制扇形统计图较合适。
故答案为:√
【点睛】
此题应根据扇形统计图各自的特点进行解答。
15.×
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】
由分析得:要想清楚地看出优优家2019年7月至12月天然气用量的增减变化情况,最好选用折线统计图。
故答案为:×
【点睛】
此题考查的是选择合适的统计图,掌握统计图的特点是解题关键。
16.√
【解析】
【分析】
根据条形统计图、折线统计图、扇形统计图的特征分析题中说法是否正确即可。
【详解】
条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图:扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系;
由上可知,题中说法正确。
故答案为:√
【点睛】
理解并掌握各统计图的特征是解答题目的关键。
17.√
【解析】
【分析】
条形统计图很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况判断即可。
【详解】
要反映学校运动会参加踢毽、跳绳、足球、乒乓球等项目的人数占总人数的百分比,选用扇形统计图比较合适。
故答案为:√
【点睛】
此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行判断。
18.√
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】
根据统计图的特点可知:
股市通常用折线统计图反映某些数据的变化情况;说法正确。
故答案为:√。
【点睛】
此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
19.统计图见详解
(1)10%
(2)200人
(3)30人
【解析】
【分析】
(1)把六年级学生最喜欢的文艺节目数量看作单位“1”,用1减去小品、歌曲、杂技和其他所占的百分比即可解答;
(2)根据已知一个数的百分之几是多少,求这个数,根据除法的意义,用除法即可求出六年级的总人数;
(3)根据求一个数的百分之几是多少,用乘法即可求出喜欢杂技节目的人数。
【详解】
(1)1-15%-15%-35%-25%
=85%-15%-35%-25%
=70%-35%-25%
=35%-25%
=10%
答:喜欢相声节目的人数占10%。
(2)70÷35%=200(人)
答:小慧所在学校六年级一共有200人。
(3)200×15%=30(人)
答:喜欢杂技节目的有30人。
【点睛】
本题考查求一个数的百分之几是多少,明确用乘法是解题的关键。
20.(1)45;
(2);25;
(3)见详解(答案不唯一)
【解析】
【分析】
(1)用总人数减去用于电话通讯、玩游戏和其他的人数即可解答。
(2)用电话通讯的人数除以调查总人数即可;用玩游戏的人数除以调查总人数再乘100%即可。
(3)根据统计图提出合理的建议即可。
【详解】
(1)200-75-50-30
=125-50-30
=75-30
=45(人)
(2)75÷200=
50÷200×100%
=0.25×100%
=25%
所以手机用于电话通讯的人数占调查总人数的,手机用于玩游戏的人数占调查总人数的25%。
(3)希望同学少玩一些游戏,多用于学习方面。
【点睛】
本题考查统计图表的综合应用。
21.(1)200人;(2)见详解;(3)375人
【解析】
【分析】
(1)把调查总人数看作单位“1”,用其他社团的人数除以其占总人数的百分率,求出总人数;
(2)根据二胡社团、古琴社团的人数及总人数,求出其占总体的百分率;根据古筝和琵琶社团占总人数的百分率和总人数,求参加古筝和琵琶社团的人数。完成统计图。
(3)根据总人数乘参加古筝社团的百分率,求参加古筝社团的人数。
【详解】
(1)(人
答:这次调查的人数一共有200人。
(2)(人
(人
统计图如下:
(3)(人
答:参加古筝社团的有375人。
【点睛】
本题主要考查统计图表的填充,关键是利用条形统计图和扇形统计图,找到解决问题的条件,计算并完成问题。
22.(1)见解析(2)40;20
【解析】
【分析】
(1)由条形统计图可知:最喜欢乒乓球的有12人,由扇形统计图可知最喜欢乒乓球的人数占总人数的30%,用12除以30%,即可求出总人数;用总人数乘上20%,即可求出最喜欢篮球的人数;用总人数乘上12.5%即可求出最喜欢跳绳的人数;然后完成条形统计图即可;
(2)最喜欢乒乓球的有12人,由扇形统计图可知最喜欢乒乓球的人数占总人数的30%,用12除以30%即可求出总人数;用喜欢踢毽子的人数除以总人数即可。
【详解】
(1)12÷30%=40(人)
40×20%=8(人)
40×12.5%=5(人)
条形统计图如下:
(2)12÷30%=40(人)
8÷40×100%
=0.2×100%
=20%
【点睛】
本题主要考查统计图表的填充,关键利用所给数据完成统计图并回答简单的问题。
23.(1)可回收垃圾;56;4
(2)23.52吨
【解析】
【分析】
(1)通过观察统计图可知,该小区产生的可回收垃圾最多,占,有害垃圾站;
(2)把小区共产生的垃圾总数看作单位“1”,根据求一个数的百分之几是多少,用乘法解答。
【详解】
(1)该小区产生的可回收垃圾最多,占,有害垃圾站。
(2)(吨
答:可回收垃圾有23.52吨。
【点睛】
此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,再根据一个数乘百分数的意义解决问题。
答案第1页,共2页
答案第15页,共17页
