25.2锐角三角形(共3课时)
图片预览




文档简介
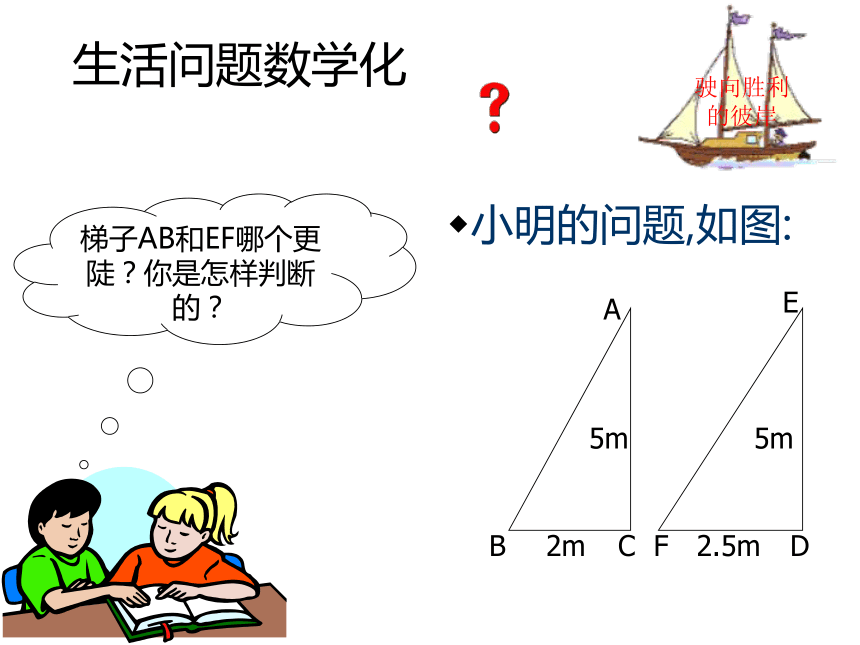
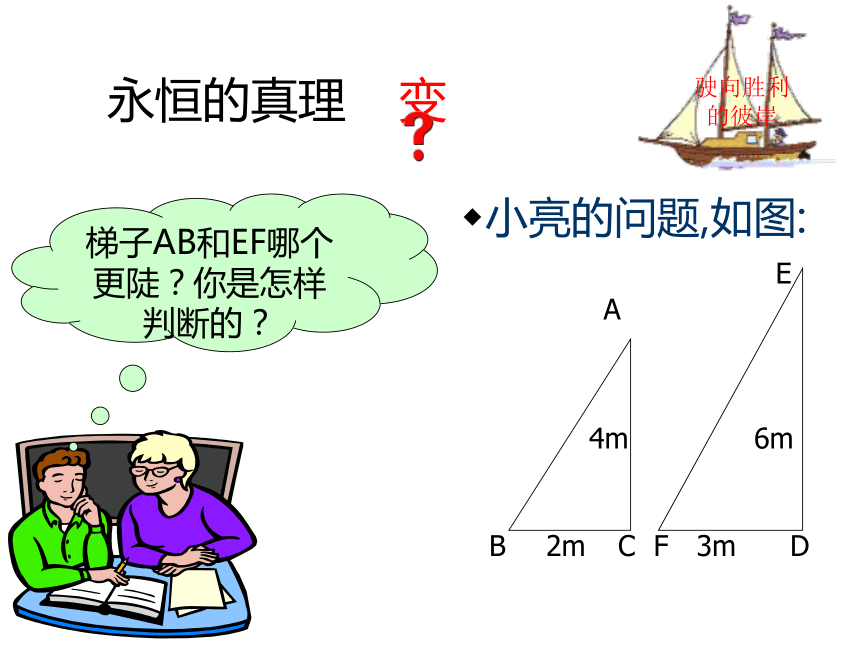
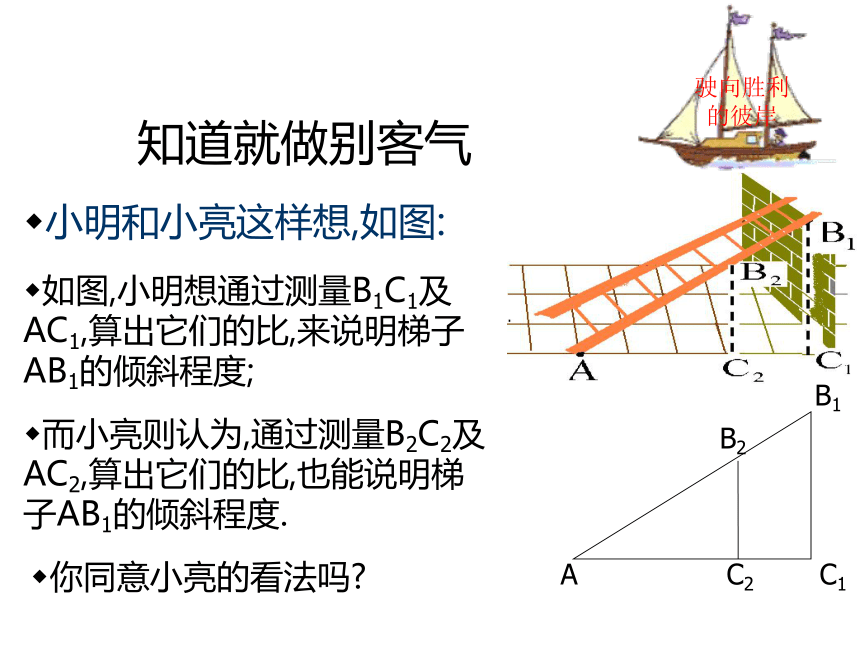
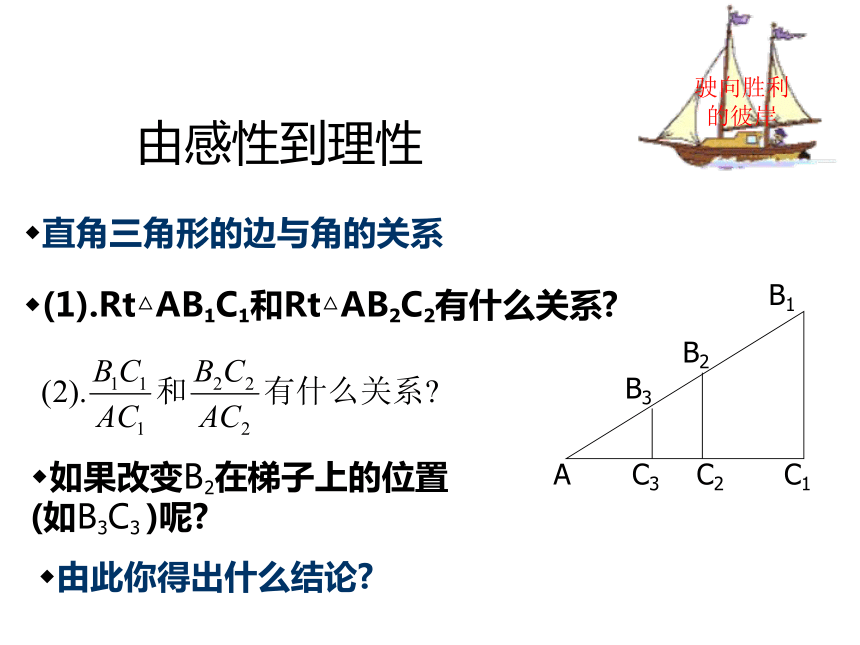
课件49张PPT。华东师大版 九年级上数学课件25.2锐角三角函数锐角三角函数的定义(第1课时)华东师大版九年级(上册)源于生活的数学梯子是我们日常生活中常见的物体驶向胜利的彼岸你能比较两个梯子哪个更陡吗?你有哪些办法?生活问题数学化小明的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?驶向胜利的彼岸有比较才有鉴别小颖的问题,如图:?驶向胜利的彼岸梯子AB和EF哪个更陡?你是怎样判断的?永恒的真理 变小亮的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?驶向胜利的彼岸在实践中探索小丽的问题,如图:驶向胜利的彼岸梯子AB和EF哪个更陡?你是怎样判断的?知道就做别客气小明和小亮这样想,如图:如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;驶向胜利的彼岸而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.你同意小亮的看法吗?由感性到理性直角三角形的边与角的关系(1).Rt△AB1C1和Rt△AB2C2有什么关系? 如果改变B2在梯子上的位置(如B3C3 )呢?由此你得出什么结论?驶向胜利的彼岸进步的标志
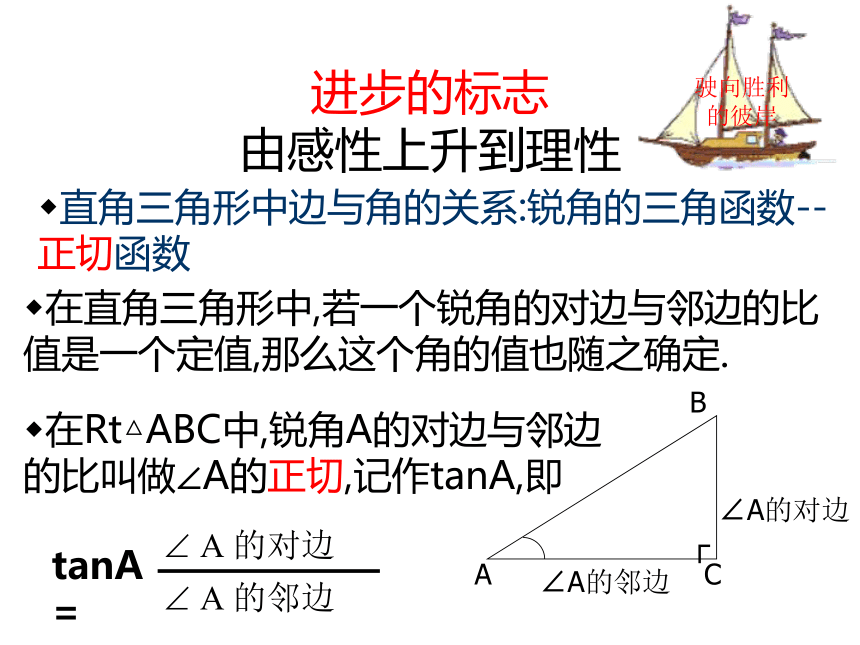
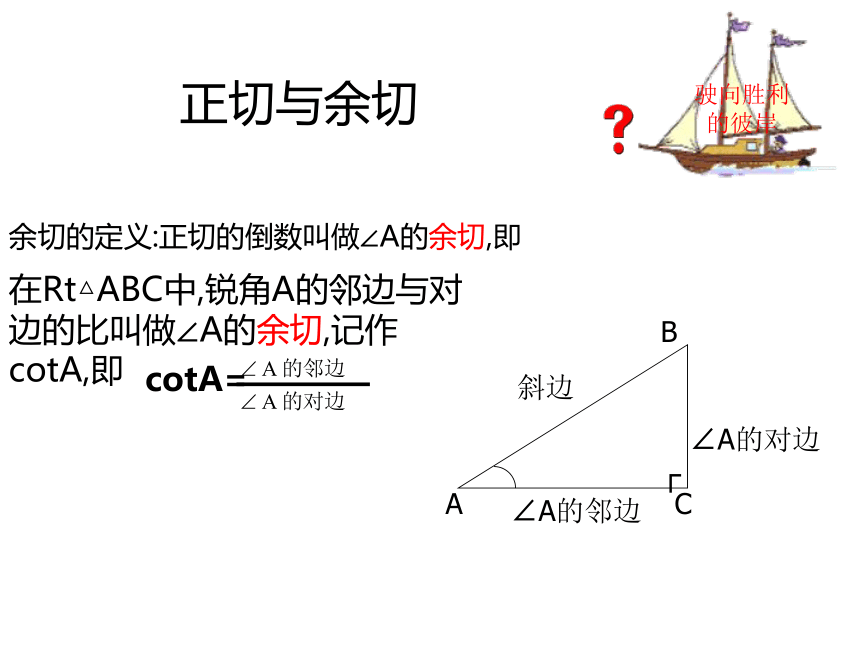
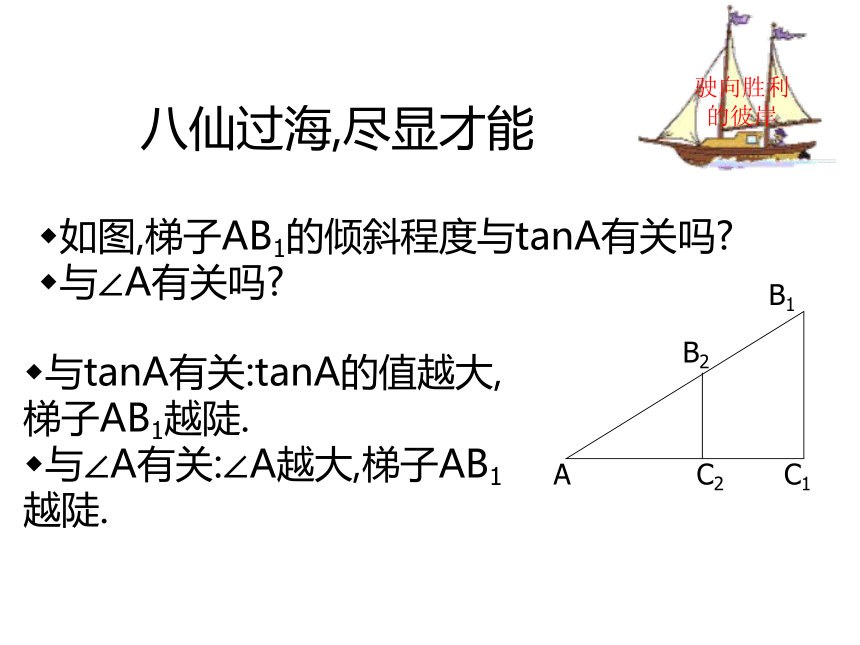
由感性上升到理性直角三角形中边与角的关系:锐角的三角函数--正切函数在直角三角形中,若一个锐角的对边与邻边的比值是一个定值,那么这个角的值也随之确定.驶向胜利的彼岸在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即正切与余切驶向胜利的彼岸余切的定义:正切的倒数叫做∠A的余切,即在Rt△ABC中,锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即八仙过海,尽显才能如图,梯子AB1的倾斜程度与tanA有关吗?
与∠A有关吗?与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.驶向胜利的彼岸行家看“门道”例1 下图表示两个自动扶梯,那一个自动扶梯比较陡?解:甲梯中,驶向胜利的彼岸乙梯中,∵tanβ>tanα,∴乙梯更陡.本领大不大 悟心来当家如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?结论:
在Rt△ABC中,如果锐角A确定时,那么∠ A的对边与斜边的比,邻边与斜边的比也随之确定.驶向胜利的彼岸正弦与余弦在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即驶向胜利的彼岸锐角A的正弦,余弦,正切和余切都叫做∠A的三角函数.生活问题数学化结论:梯子的倾斜程度与sinA和cosA有关:
sinA越大,梯子越陡;cosA越小,样子越陡.如图,梯子的倾斜程度与sinA和cosA有关吗?驶向胜利的彼岸行家看“门道”例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
求:BC的长.驶向胜利的彼岸老师期望:
请你求出cosA,tanA,sinC,cosC和tanC的值.你敢应战吗?解:在Rt△ABC中, 八仙过海,尽显才能1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).驶向胜利的彼岸八仙过海,尽显才能3.鉴宝专家—--是真是假:你能从中悟出点东西?驶向胜利的彼岸八仙过海,尽显才能4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.驶向胜利的彼岸八仙过海,尽显才能6.如图, ∠C=90°CD⊥AB.7.在上图中,若BD=6,CD=12.求tanA cosA的值.驶向胜利的彼岸老师提示:
模型“双垂直三角形”的有关性质你可曾记得.八仙过海,尽显才能8.如图,分别根据图(1)和图(2)求tanA和 cosA的值.9.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA、tanB、
sinB 和cosA
(2)BC=3,tanA= ,求AC和AB.驶向胜利的彼岸老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.八仙过海,尽显才能10.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC、BC和sinB 、cotA.11.在等腰△ABC中,AB=AC=13,BC=10,
求∠B的四个三角函数值.驶向胜利的彼岸提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.相信自己12. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求sinA,cosA,tanA,cotA和sinB,cosB,tanB,cotB.
(2)BC=3,sinA=0.6,求AC 和AB.
(3)AC=4,cosA=0.8,求BC.13.在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18.
求:sinB,cosB,tanB,cotB.驶向胜利的彼岸提示:
作梯形的高是梯形的常用辅助,借助它可以转化为直角三角形.回味无穷回顾,反思,深化1.锐角三角函数定义:驶向胜利的彼岸请思考:在Rt△ABC中,
sinA和cosB有什么关系? tanA和cotB有什么关系?
你能写出它们的关系吗?回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA,cotA是在直角三角形中定义的,
∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA,cotA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.sinA,cosA,tanA,cotA是一个比值.注意比的顺序,且sinA,cosA,tanA,cotA均﹥0,无单位.
4.sinA,cosA,tanA,cotA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.驶向胜利的彼岸25.2锐角三角函数(第2课时)华东师大版九年级(上册)在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 锐角三角函数的意义回顾:(1)0<sin A<1,0<cos A<1,(3)tan A?cot A=1锐角三角函数的意义
回顾:(2) tanA>0,cotA>0基础练习1.在Rt△ABC中,∠C=90゜,∠A、∠B、∠C的对边分别为a、b、c,下列式子中一定成立的是( )
A.a=c·cosB
B.a= b· cosB
C.a=c · tanB
D.a=b · tanB基础练习3.在△ABC中,∠C=90°,BC=3,tanB=
则AB= 。
2.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )。
A sinA= B cosA= C tanA= D cotA=基础练习 设Rt△ABC中,∠C=90゜,∠A、∠B、∠C的对边分别为a、b、c,根据下列所给条件求∠B的四个三角函数值.
(1) ∠A=45°, (2) ∠B=30° 试一试结论:在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半.做一做我们把30゜、45゜、60゜的三角函数值列表如下.
(请填出空白处的值) (1)2cos60゜+2sin30゜+4tan45゜ ;
(2) sin30゜+sin245゜-tan260゜.例1 求值:例2 根据下列条件,求出相应的锐角α:
例 3解:练 习4.求值:2cos60°+2 sin30°+4tan45° 拓 展锐角三角函数的意义
特殊角度的三角函数值小结11(第3课时)华东师大版九年级(上册)25.3锐角三角函数引 入 如图,有一个斜坡,现在要在斜坡AB上植树造林,要保持两棵树水平间距为2m,那么沿斜坡方向每隔几米挖坑(已知斜坡面的倾斜角为16018‘)这是一个实际问题,
同学们想一想
能求出两坑的距离吗?求已知锐角的三角函数值:求sin63゜52′41″的值(精确到0.0001)
求cot70゜45′的值(精确到0.0001)
练 习 1
使用计算器求下列三角函数值(精确到0.0001)
sin24゜, cos51゜42′20″,
tαn70゜21′ ,cot70゜.例1 例2 已知tan x=0.7410,求锐角x(精确到1′)
已知cot x=0.1950,求锐角x.(精确到1′)
练 习 2
已知锐角α的三角函数值,使用计算器求锐角α(精确到1′)
(1)sin α=0.2476;
(2)cosα=0.4174;
(3)tan α=0.1890;
(4)cot α=1.3773.通过观察、比较,你能对下列问题给出结论吗?
1、当角度增大时,sinα,cosα,tanα,的变化情况.
2、试分别比较当0°<α< 45°,45 °<α<90 °时
sinα cosα
练习3 1、在Rt△ABC中,∠C=90゜,
已知AC=21,AB=29,
求∠A的度数
2. 在Rt△ABC中,∠C=90゜,BC:AC=3:4,求∠B的度数能力拓展题 已知:直角三角形ABC中,∠C=900,∠BAC=300,延长CA到D使AD=AB,连接BD,你能运用三角函数求出∠D的正切、余切值吗?
?小 结 通过本节课的学习,掌握了哪些知识,还有哪些疑惑!
与∠A有关吗?与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.驶向胜利的彼岸行家看“门道”例1 下图表示两个自动扶梯,那一个自动扶梯比较陡?解:甲梯中,驶向胜利的彼岸乙梯中,∵tanβ>tanα,∴乙梯更陡.本领大不大 悟心来当家如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?结论:
在Rt△ABC中,如果锐角A确定时,那么∠ A的对边与斜边的比,邻边与斜边的比也随之确定.驶向胜利的彼岸正弦与余弦在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即驶向胜利的彼岸锐角A的正弦,余弦,正切和余切都叫做∠A的三角函数.生活问题数学化结论:梯子的倾斜程度与sinA和cosA有关:
sinA越大,梯子越陡;cosA越小,样子越陡.如图,梯子的倾斜程度与sinA和cosA有关吗?驶向胜利的彼岸行家看“门道”例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
求:BC的长.驶向胜利的彼岸老师期望:
请你求出cosA,tanA,sinC,cosC和tanC的值.你敢应战吗?解:在Rt△ABC中, 八仙过海,尽显才能1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).驶向胜利的彼岸八仙过海,尽显才能3.鉴宝专家—--是真是假:你能从中悟出点东西?驶向胜利的彼岸八仙过海,尽显才能4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.驶向胜利的彼岸八仙过海,尽显才能6.如图, ∠C=90°CD⊥AB.7.在上图中,若BD=6,CD=12.求tanA cosA的值.驶向胜利的彼岸老师提示:
模型“双垂直三角形”的有关性质你可曾记得.八仙过海,尽显才能8.如图,分别根据图(1)和图(2)求tanA和 cosA的值.9.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA、tanB、
sinB 和cosA
(2)BC=3,tanA= ,求AC和AB.驶向胜利的彼岸老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.八仙过海,尽显才能10.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC、BC和sinB 、cotA.11.在等腰△ABC中,AB=AC=13,BC=10,
求∠B的四个三角函数值.驶向胜利的彼岸提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.相信自己12. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求sinA,cosA,tanA,cotA和sinB,cosB,tanB,cotB.
(2)BC=3,sinA=0.6,求AC 和AB.
(3)AC=4,cosA=0.8,求BC.13.在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18.
求:sinB,cosB,tanB,cotB.驶向胜利的彼岸提示:
作梯形的高是梯形的常用辅助,借助它可以转化为直角三角形.回味无穷回顾,反思,深化1.锐角三角函数定义:驶向胜利的彼岸请思考:在Rt△ABC中,
sinA和cosB有什么关系? tanA和cotB有什么关系?
你能写出它们的关系吗?回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA,cotA是在直角三角形中定义的,
∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA,cotA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.sinA,cosA,tanA,cotA是一个比值.注意比的顺序,且sinA,cosA,tanA,cotA均﹥0,无单位.
4.sinA,cosA,tanA,cotA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.驶向胜利的彼岸25.2锐角三角函数(第2课时)华东师大版九年级(上册)在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 锐角三角函数的意义回顾:(1)0<sin A<1,0<cos A<1,(3)tan A?cot A=1锐角三角函数的意义
回顾:(2) tanA>0,cotA>0基础练习1.在Rt△ABC中,∠C=90゜,∠A、∠B、∠C的对边分别为a、b、c,下列式子中一定成立的是( )
A.a=c·cosB
B.a= b· cosB
C.a=c · tanB
D.a=b · tanB基础练习3.在△ABC中,∠C=90°,BC=3,tanB=
则AB= 。
2.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )。
A sinA= B cosA= C tanA= D cotA=基础练习 设Rt△ABC中,∠C=90゜,∠A、∠B、∠C的对边分别为a、b、c,根据下列所给条件求∠B的四个三角函数值.
(1) ∠A=45°, (2) ∠B=30° 试一试结论:在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半.做一做我们把30゜、45゜、60゜的三角函数值列表如下.
(请填出空白处的值) (1)2cos60゜+2sin30゜+4tan45゜ ;
(2) sin30゜+sin245゜-tan260゜.例1 求值:例2 根据下列条件,求出相应的锐角α:
例 3解:练 习4.求值:2cos60°+2 sin30°+4tan45° 拓 展锐角三角函数的意义
特殊角度的三角函数值小结11(第3课时)华东师大版九年级(上册)25.3锐角三角函数引 入 如图,有一个斜坡,现在要在斜坡AB上植树造林,要保持两棵树水平间距为2m,那么沿斜坡方向每隔几米挖坑(已知斜坡面的倾斜角为16018‘)这是一个实际问题,
同学们想一想
能求出两坑的距离吗?求已知锐角的三角函数值:求sin63゜52′41″的值(精确到0.0001)
求cot70゜45′的值(精确到0.0001)
练 习 1
使用计算器求下列三角函数值(精确到0.0001)
sin24゜, cos51゜42′20″,
tαn70゜21′ ,cot70゜.例1 例2 已知tan x=0.7410,求锐角x(精确到1′)
已知cot x=0.1950,求锐角x.(精确到1′)
练 习 2
已知锐角α的三角函数值,使用计算器求锐角α(精确到1′)
(1)sin α=0.2476;
(2)cosα=0.4174;
(3)tan α=0.1890;
(4)cot α=1.3773.通过观察、比较,你能对下列问题给出结论吗?
1、当角度增大时,sinα,cosα,tanα,的变化情况.
2、试分别比较当0°<α< 45°,45 °<α<90 °时
sinα cosα
练习3 1、在Rt△ABC中,∠C=90゜,
已知AC=21,AB=29,
求∠A的度数
2. 在Rt△ABC中,∠C=90゜,BC:AC=3:4,求∠B的度数能力拓展题 已知:直角三角形ABC中,∠C=900,∠BAC=300,延长CA到D使AD=AB,连接BD,你能运用三角函数求出∠D的正切、余切值吗?
?小 结 通过本节课的学习,掌握了哪些知识,还有哪些疑惑!
