人教A版(2019)选择性必修第二册5.2.2导数的四则运算法则 课件(共15张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册5.2.2导数的四则运算法则 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 00:00:00 | ||
图片预览




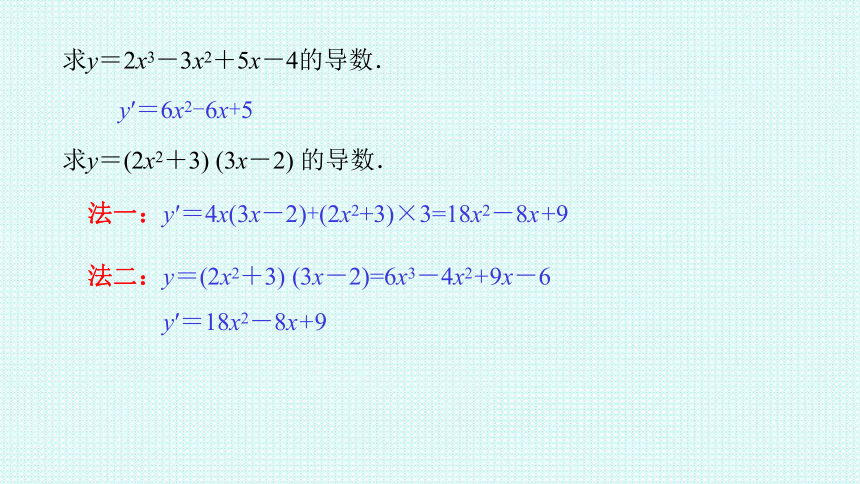


文档简介
(共15张PPT)
5.2.2 导数的四则运算法则
新课程标准解读 核心素养
1.类比代数和向量的四则运算法则,感受导数的四则运算法则,体会导数运算是导数工具性作用的基础. 2.会用导数的四则运算法则求解相关问题. 数学运算:导数的运算.
情境导入
高铁是目前一种非常受欢迎的交通工具,既低碳又快捷.设一高铁走过的路程s(单位:m)关于时间t(单位:s)的函数为s=f(t),求它的瞬时速度,就是求f(t)的导数.根据导数的定义,就是求当Δt→0时, 所趋近的那个定值.运算比较复杂,而且有的函数,如y=sin x+x很难运用定义求导数.
是否有更简便的求导数的方法呢?
导数的四则运算法则
f(x),g(x)是可导的.
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
[f(x)±g(x)]′=f′(x)±g′(x)
求y=x3+sinx的导数.
y′=3x2+cosx
求y=x4-x2-x+3的导数.
y′=4x3-2x-1
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)
推论:常数与函数的积的导数,等于常数乘函数的导数,即:
求y=2x3-3x2+5x-4的导数.
y′=6x2-6x+5
求y=(2x2+3) (3x-2) 的导数.
法一:y′=4x(3x-2)+(2x2+3)×3=18x2-8x+9
法二:y=(2x2+3) (3x-2)=6x3-4x2+9x-6
y′=18x2-8x+9
法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
=
求函数y= 的导数.
1
x
y′=
x2
0-1
=-
1
x2
求函数y=tanx的导数.
y′=(tanx)′
sinx
cosx
=( )′
cos2x
=
cos2x+sin2x
cos2x
=
1
求函数y= 的导数.
x+1
x-1
y′=( )′=
x+1
x-1
(x+1)2
x+1-(x-1)
(x+1)2
2
=
应用导数公式的注意事项
(1)两个导数的和差运算只可推广到有限个函数的和差的导数运算,即[u(x)±v(x)±…±w(x)]′=u′(x)±v′(x)±…±w′(x);
(2)两个函数可导,则它们的和、差、积、商(商的分母不为零)必可导.同上可推广到有限个函数的函数乘积的导数即:①[af(x)+bg(x)]′=af′(x)+bg′(x);②[u(x)v(x)…w(x)]′=u′(x)v(x)…w(x)+u(x)v′(x)…w(x)+…+u(x)v(x)…w′(x);
(3)若两个函数不可导,则它们的和、差、积、商不一定不可导;
(4)对于较复杂的函数式,应先进行适当的化简变形,化为较简单的函数式后再求导,可简化求导过程.
题型一 利用导数的四则运算法则求导
(1)y′=2x-2x-3.
(2)y′=(ln 3+1)·(3e)x-2xln 2.
题型二 导数几何意义的综合应用
例2(链接教科书第78页练习3题)(1)曲线y=
的切线的斜率为 ( )
(1)y′=
(2)设曲线y=xln x在点(x0,y0)处的切线与直线x-y-2=0平行.
∵y′=ln x+1,∴y′|x=x0=ln x0+1=1,解得x0=1,
∴y0=0,即切点坐标为(1,0).∴切点(1,0)到直线x-y-2=0的距离为
即曲线y=xln x上的点到直线x-y-2=0
1.此类问题往往涉及切点、切点处的导数、切线方程三个主要元素,其他的条件可以进行转化,从而转化为这三个要素间的关系.
2.准确利用求导法则求出导函数是解决此类问题的第一步,也是解题的关键,务必做到准确.
3.分清已知点是否在曲线上,若不在曲线上,则要设出切点,这是解题时的易错点.
通性通法
∴切线方程为y=2(x-1),即2x-y-2=0.
令x=0得y=-2;令y=0得x=1.
在点(1,0)处
的切线与坐标轴围成的面积为
题型三 利用函数的导数求参数
例3(1)(2019·全国卷Ⅲ)已知曲线y=aex+xln x在点(1,ae)处的切线方程为y=2x+b,则 ( )
A.a=e,b=-1 B.a=e,b=1
C.a=e-1,b=1 D.a=e-1,b=-1
(1)y′=aex+ln x+1,k=y′|x=1=ae+1,∴ 切线方程为
y-ae=(ae+1)(x-1),即y=(ae+1)x-1.
又∵ 切线方程为y=2x+b,
即a=e-1,b=-1
(2)已知函数f(x)=ax3+bx2+cx的图象过点(1,5),其导函数
y=f′(x)的图象如图所示,则函数f(x)的解析式为________.
o
x
y
1
2
(2)∵f′(x)=3ax2+2bx+c,f′(1)=0,f′(2)=0,f(1)=5,
故函数f(x)的解析式是f(x)=2x3-9x2+12x.
(2021·黑龙江鹤岗市第一中学高二期末)已知f(x)=x2+2xf′(1),
则f′(0)=________.
因为f(x)=x2+2xf′(1),所以f′(x)=2x+2f′(1).令x=1,得f′(1)=2×1+2f′(1),解得f′(1)=-2,所以f′(x)=2x-4,所以f′(0)=2×0-4=-4.
的切线与直线x+ay+1=0垂直,
则a=________.
a=1.
5.2.2 导数的四则运算法则
新课程标准解读 核心素养
1.类比代数和向量的四则运算法则,感受导数的四则运算法则,体会导数运算是导数工具性作用的基础. 2.会用导数的四则运算法则求解相关问题. 数学运算:导数的运算.
情境导入
高铁是目前一种非常受欢迎的交通工具,既低碳又快捷.设一高铁走过的路程s(单位:m)关于时间t(单位:s)的函数为s=f(t),求它的瞬时速度,就是求f(t)的导数.根据导数的定义,就是求当Δt→0时, 所趋近的那个定值.运算比较复杂,而且有的函数,如y=sin x+x很难运用定义求导数.
是否有更简便的求导数的方法呢?
导数的四则运算法则
f(x),g(x)是可导的.
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
[f(x)±g(x)]′=f′(x)±g′(x)
求y=x3+sinx的导数.
y′=3x2+cosx
求y=x4-x2-x+3的导数.
y′=4x3-2x-1
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)
推论:常数与函数的积的导数,等于常数乘函数的导数,即:
求y=2x3-3x2+5x-4的导数.
y′=6x2-6x+5
求y=(2x2+3) (3x-2) 的导数.
法一:y′=4x(3x-2)+(2x2+3)×3=18x2-8x+9
法二:y=(2x2+3) (3x-2)=6x3-4x2+9x-6
y′=18x2-8x+9
法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
=
求函数y= 的导数.
1
x
y′=
x2
0-1
=-
1
x2
求函数y=tanx的导数.
y′=(tanx)′
sinx
cosx
=( )′
cos2x
=
cos2x+sin2x
cos2x
=
1
求函数y= 的导数.
x+1
x-1
y′=( )′=
x+1
x-1
(x+1)2
x+1-(x-1)
(x+1)2
2
=
应用导数公式的注意事项
(1)两个导数的和差运算只可推广到有限个函数的和差的导数运算,即[u(x)±v(x)±…±w(x)]′=u′(x)±v′(x)±…±w′(x);
(2)两个函数可导,则它们的和、差、积、商(商的分母不为零)必可导.同上可推广到有限个函数的函数乘积的导数即:①[af(x)+bg(x)]′=af′(x)+bg′(x);②[u(x)v(x)…w(x)]′=u′(x)v(x)…w(x)+u(x)v′(x)…w(x)+…+u(x)v(x)…w′(x);
(3)若两个函数不可导,则它们的和、差、积、商不一定不可导;
(4)对于较复杂的函数式,应先进行适当的化简变形,化为较简单的函数式后再求导,可简化求导过程.
题型一 利用导数的四则运算法则求导
(1)y′=2x-2x-3.
(2)y′=(ln 3+1)·(3e)x-2xln 2.
题型二 导数几何意义的综合应用
例2(链接教科书第78页练习3题)(1)曲线y=
的切线的斜率为 ( )
(1)y′=
(2)设曲线y=xln x在点(x0,y0)处的切线与直线x-y-2=0平行.
∵y′=ln x+1,∴y′|x=x0=ln x0+1=1,解得x0=1,
∴y0=0,即切点坐标为(1,0).∴切点(1,0)到直线x-y-2=0的距离为
即曲线y=xln x上的点到直线x-y-2=0
1.此类问题往往涉及切点、切点处的导数、切线方程三个主要元素,其他的条件可以进行转化,从而转化为这三个要素间的关系.
2.准确利用求导法则求出导函数是解决此类问题的第一步,也是解题的关键,务必做到准确.
3.分清已知点是否在曲线上,若不在曲线上,则要设出切点,这是解题时的易错点.
通性通法
∴切线方程为y=2(x-1),即2x-y-2=0.
令x=0得y=-2;令y=0得x=1.
在点(1,0)处
的切线与坐标轴围成的面积为
题型三 利用函数的导数求参数
例3(1)(2019·全国卷Ⅲ)已知曲线y=aex+xln x在点(1,ae)处的切线方程为y=2x+b,则 ( )
A.a=e,b=-1 B.a=e,b=1
C.a=e-1,b=1 D.a=e-1,b=-1
(1)y′=aex+ln x+1,k=y′|x=1=ae+1,∴ 切线方程为
y-ae=(ae+1)(x-1),即y=(ae+1)x-1.
又∵ 切线方程为y=2x+b,
即a=e-1,b=-1
(2)已知函数f(x)=ax3+bx2+cx的图象过点(1,5),其导函数
y=f′(x)的图象如图所示,则函数f(x)的解析式为________.
o
x
y
1
2
(2)∵f′(x)=3ax2+2bx+c,f′(1)=0,f′(2)=0,f(1)=5,
故函数f(x)的解析式是f(x)=2x3-9x2+12x.
(2021·黑龙江鹤岗市第一中学高二期末)已知f(x)=x2+2xf′(1),
则f′(0)=________.
因为f(x)=x2+2xf′(1),所以f′(x)=2x+2f′(1).令x=1,得f′(1)=2×1+2f′(1),解得f′(1)=-2,所以f′(x)=2x-4,所以f′(0)=2×0-4=-4.
的切线与直线x+ay+1=0垂直,
则a=________.
a=1.
