人教A版(2019)选择性必修第三册6.1.1分类加法计数原理与分步乘法计数原理 课件(共17张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册6.1.1分类加法计数原理与分步乘法计数原理 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 20:32:21 | ||
图片预览






文档简介
(共17张PPT)
6.1.1分类加法计数原理与分步乘法计数原理
新课程标准解读 核心素养
1.根据实际问题归纳出两个计数原理,要正确理解“完成一件事”的含义,会应用两个计数原理解决问题. 2.根据实际问题的特征,能正确区分“分类”与“分步”:分类着重在“类”,类与类之间是并列的、互斥的、独立的;分步强调的是“步”,步与步之间是连续的、缺一不可的. 逻辑推理、数学运算:通过实例了解两个原理的意义及作用,解决相关问题.
情境导入
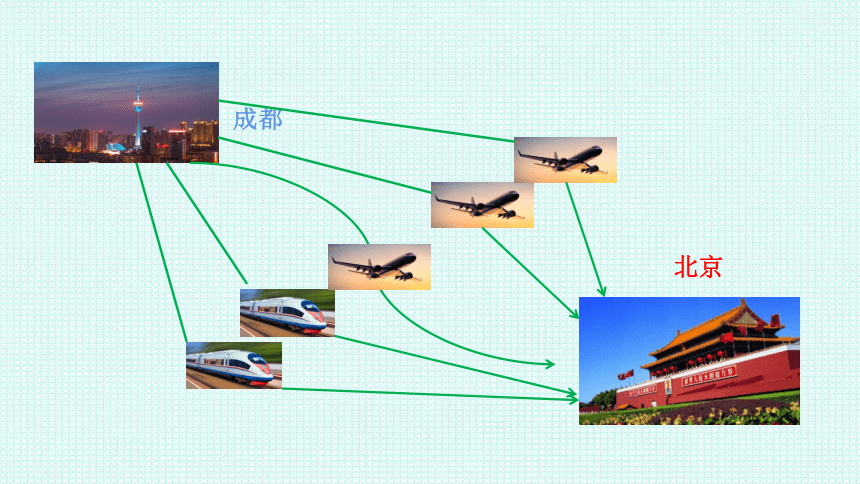
2022年2月4日第24届冬季奥林匹克运动会将在北京和张家口市联合举行,这是体坛的一大盛事,一名志愿者从成都赴北京为奥运会服务,从成都到北京每天有3个航班,2列火车.该志愿者从成都到北京的方案可以分为几类?在这几类中各有几种方法?该志愿者从成都到北京共有多少种不同的方法?
成都
北京
探究点1 分类加法计数原理
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
提示:因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+10=36种不同的号码.
问题2 用一个大写的英文字母和一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
260种
分类加法计数原理
(1)完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法.
(1)核心:原理的核心为“分类”,完成一件事的方法为若干类.
(2)特点:相互独立;各类方案相互独立,各类方案中的各种方法也相互独立,并且用任何一类方法都可以独立完成这件事.
(2)分类加法计数原理的推广
如果完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有N=m1+m2+m3+…+mn种不同的方法.
例1.在填写高考志愿表时,一名高中毕业生了解到,A、B两所大学各有一些自己感兴趣的强项专业,如表6.1-1.
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
这名同学在A大学中有5种专业选择,在B大学中有4种专业选择,根据分类计数原理:这名同学可能的专业选择共有:N=5+4=9种
利用分类加法计数原理解题的一般思路
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
某校高一年级共8个班,高二年级共9个班,从中选一个班级担任学校星期一早晨升旗任务,安排方法共有( )
A.8种 B.9种
C.17种 D.72种
探究点2 分步乘法计数原理
思考:用前6个大写的英文字母和1~9个阿拉伯数字,以A1, A1,…A9,B1,B2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
A
1
2
3
4
5
6
7
8
9
树形图
A1
A2
A3
A4
A5
A6
A7
A8
A9
由于前6个英文字母的任意一个都能和9个数字中的任何一个组成一个号码,而且它们各不相同,因此共有6×9=54个不同的号码.
B1
B2
B3
B4
B5
B6
B7
B8
B9
C1
C2
C3
C4
C5
C6
C7
C8
C9
…
上述计数过程的基本环节是:
(1)由问题条件中的“和”,可确定完成编号要分两步;
(2)分别计算各步号码的个数;
(3)将各步号码的个数相乘,得出所有号码的个数.
分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法.
(1)明确题目中的“完成这件事”是什么,确定完成这件事需要几个步骤,且每步都是独立的.
(2)将完成这件事划分为几个步骤,各步骤之间有一定的连续性,只有当所有步骤都完成了,整个事件才算完成.
(3)计算公式的推广:完成一件事需要n个步骤,做第1步有m1种方法,做第2步有m2种方法,……,做第n步有mn种方法,完成这件事共有N=m1×m2×…×mn种方法.
例2 某班有男生30名,女生24名。从中选出男、女生各1名代表班级参加比赛,共有多少种不同的选法?
分析 要完成的一件事是“选男生和女生各1名”,可分两步:第一步, 选男生;第二步,选女生.
解 第1步,从30名男生中选出1人,有30种不同选择;
第2步,从24名女生中选出1人,有24种不同选择;
根据分步计数原理,共有 30×24=720种不同方法.
例3 书架上第1层放有4本不同的计算机书,第 2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法
(2)从书架的第1、 2、 3层各取1本书,有多少种不同取法
解:(1)根据分类加法计数原理可得:N=4+3+2=9;
(2)根据分步乘法计数原理可得:N=4 ×3×2=24.
已知x∈{1,2,3},y∈{2,-4,8},则x·y可表示不同的值的个数为________.
因为从集合{1,2,3}中任取x,所以有3种取法,y从{2,-4,8}中任取一个有3种取法,故x·y可表示3×3=9个不同的值.
分类计数与分步计数原理的区别和联系
加法原理 乘法原理
联系
分类计数原理和分步计数原理,回答的都是关于完成一件事情的不同方法的种数的问题。
区别
完成一件事情共有n类
办法,关键词是“分类”
完成一件事情,共分n个
步骤,关键词是“分步”
每类办法都能独立完成这件事情。
每一步得到的只是中间结果,任何一步都不能能独立完成,这件事情,缺少任何一步也不能完成这件事情,只有每个步骤完成了,才能完成这件事情。
各类办法是互斥的、
并列的、独立的
各步之间是相关联的
例4 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法?
分析 要完成的一件事是“从3幅画中选出2幅,并分别挂在左、右两边墙上”,可以分步完成。
解 从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第1步,从3幅画中选1幅挂在左边墙上,有3种选法;
第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法,
根据分步乘法计数原理,不同挂法的种数为N=3×2=6.
左边
右边
得到的挂法
甲
乙
丙
乙
甲
丙
丙
甲
乙
左甲右乙
左甲右丙
左乙右甲
左乙右丙
左丙右甲
左丙右乙
1).某城市的部分电话号码是0632-369××××,后面每个数字来自0~9这10个数,问可以产生多少个不同的电话号码
10×10×10×10=104
2).若要求最后4个数字不重复,则又有多少种不同的电话号码
10×9×8×7=5040
3.随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容.交通管理部门出台了一种汽车牌照组成方法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照?
共能给:26×25×24×10×9×8×2=22464000
4.从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a,b,组成复数a+bi,其中虚数有( )
A.36个 B.42个 C.30个 D.35个
∵a,b互不相等且为虚数,∴所有b只能从{1,2,3,4,5,6}中选一个,有6种,a从剩余的6个选一个,有6种,
∴根据分步乘法计数原理知虚数有6×6=36(个).
课堂小结
1.分类计数原理加法与分步乘法计数原理的异同
加法计数原理:针对的是“分类”问题.各类方法相互独立.
乘法计数原理:针对的是“分步”问题。 每步相互依存。
2.分类加法计数原理与分步乘法计数原理的方法技巧
分类要做到“不重不漏”
分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”
完成了所有步骤 ,恰好完成任务,当然步与步之间要相互独 立 .分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步方法数相乘,得到总数.
6.1.1分类加法计数原理与分步乘法计数原理
新课程标准解读 核心素养
1.根据实际问题归纳出两个计数原理,要正确理解“完成一件事”的含义,会应用两个计数原理解决问题. 2.根据实际问题的特征,能正确区分“分类”与“分步”:分类着重在“类”,类与类之间是并列的、互斥的、独立的;分步强调的是“步”,步与步之间是连续的、缺一不可的. 逻辑推理、数学运算:通过实例了解两个原理的意义及作用,解决相关问题.
情境导入
2022年2月4日第24届冬季奥林匹克运动会将在北京和张家口市联合举行,这是体坛的一大盛事,一名志愿者从成都赴北京为奥运会服务,从成都到北京每天有3个航班,2列火车.该志愿者从成都到北京的方案可以分为几类?在这几类中各有几种方法?该志愿者从成都到北京共有多少种不同的方法?
成都
北京
探究点1 分类加法计数原理
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
提示:因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+10=36种不同的号码.
问题2 用一个大写的英文字母和一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
260种
分类加法计数原理
(1)完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法.
(1)核心:原理的核心为“分类”,完成一件事的方法为若干类.
(2)特点:相互独立;各类方案相互独立,各类方案中的各种方法也相互独立,并且用任何一类方法都可以独立完成这件事.
(2)分类加法计数原理的推广
如果完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有N=m1+m2+m3+…+mn种不同的方法.
例1.在填写高考志愿表时,一名高中毕业生了解到,A、B两所大学各有一些自己感兴趣的强项专业,如表6.1-1.
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
这名同学在A大学中有5种专业选择,在B大学中有4种专业选择,根据分类计数原理:这名同学可能的专业选择共有:N=5+4=9种
利用分类加法计数原理解题的一般思路
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
某校高一年级共8个班,高二年级共9个班,从中选一个班级担任学校星期一早晨升旗任务,安排方法共有( )
A.8种 B.9种
C.17种 D.72种
探究点2 分步乘法计数原理
思考:用前6个大写的英文字母和1~9个阿拉伯数字,以A1, A1,…A9,B1,B2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
A
1
2
3
4
5
6
7
8
9
树形图
A1
A2
A3
A4
A5
A6
A7
A8
A9
由于前6个英文字母的任意一个都能和9个数字中的任何一个组成一个号码,而且它们各不相同,因此共有6×9=54个不同的号码.
B1
B2
B3
B4
B5
B6
B7
B8
B9
C1
C2
C3
C4
C5
C6
C7
C8
C9
…
上述计数过程的基本环节是:
(1)由问题条件中的“和”,可确定完成编号要分两步;
(2)分别计算各步号码的个数;
(3)将各步号码的个数相乘,得出所有号码的个数.
分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法.
(1)明确题目中的“完成这件事”是什么,确定完成这件事需要几个步骤,且每步都是独立的.
(2)将完成这件事划分为几个步骤,各步骤之间有一定的连续性,只有当所有步骤都完成了,整个事件才算完成.
(3)计算公式的推广:完成一件事需要n个步骤,做第1步有m1种方法,做第2步有m2种方法,……,做第n步有mn种方法,完成这件事共有N=m1×m2×…×mn种方法.
例2 某班有男生30名,女生24名。从中选出男、女生各1名代表班级参加比赛,共有多少种不同的选法?
分析 要完成的一件事是“选男生和女生各1名”,可分两步:第一步, 选男生;第二步,选女生.
解 第1步,从30名男生中选出1人,有30种不同选择;
第2步,从24名女生中选出1人,有24种不同选择;
根据分步计数原理,共有 30×24=720种不同方法.
例3 书架上第1层放有4本不同的计算机书,第 2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法
(2)从书架的第1、 2、 3层各取1本书,有多少种不同取法
解:(1)根据分类加法计数原理可得:N=4+3+2=9;
(2)根据分步乘法计数原理可得:N=4 ×3×2=24.
已知x∈{1,2,3},y∈{2,-4,8},则x·y可表示不同的值的个数为________.
因为从集合{1,2,3}中任取x,所以有3种取法,y从{2,-4,8}中任取一个有3种取法,故x·y可表示3×3=9个不同的值.
分类计数与分步计数原理的区别和联系
加法原理 乘法原理
联系
分类计数原理和分步计数原理,回答的都是关于完成一件事情的不同方法的种数的问题。
区别
完成一件事情共有n类
办法,关键词是“分类”
完成一件事情,共分n个
步骤,关键词是“分步”
每类办法都能独立完成这件事情。
每一步得到的只是中间结果,任何一步都不能能独立完成,这件事情,缺少任何一步也不能完成这件事情,只有每个步骤完成了,才能完成这件事情。
各类办法是互斥的、
并列的、独立的
各步之间是相关联的
例4 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法?
分析 要完成的一件事是“从3幅画中选出2幅,并分别挂在左、右两边墙上”,可以分步完成。
解 从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第1步,从3幅画中选1幅挂在左边墙上,有3种选法;
第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法,
根据分步乘法计数原理,不同挂法的种数为N=3×2=6.
左边
右边
得到的挂法
甲
乙
丙
乙
甲
丙
丙
甲
乙
左甲右乙
左甲右丙
左乙右甲
左乙右丙
左丙右甲
左丙右乙
1).某城市的部分电话号码是0632-369××××,后面每个数字来自0~9这10个数,问可以产生多少个不同的电话号码
10×10×10×10=104
2).若要求最后4个数字不重复,则又有多少种不同的电话号码
10×9×8×7=5040
3.随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容.交通管理部门出台了一种汽车牌照组成方法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照?
共能给:26×25×24×10×9×8×2=22464000
4.从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a,b,组成复数a+bi,其中虚数有( )
A.36个 B.42个 C.30个 D.35个
∵a,b互不相等且为虚数,∴所有b只能从{1,2,3,4,5,6}中选一个,有6种,a从剩余的6个选一个,有6种,
∴根据分步乘法计数原理知虚数有6×6=36(个).
课堂小结
1.分类计数原理加法与分步乘法计数原理的异同
加法计数原理:针对的是“分类”问题.各类方法相互独立.
乘法计数原理:针对的是“分步”问题。 每步相互依存。
2.分类加法计数原理与分步乘法计数原理的方法技巧
分类要做到“不重不漏”
分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”
完成了所有步骤 ,恰好完成任务,当然步与步之间要相互独 立 .分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步方法数相乘,得到总数.
