人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共22张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 20:38:37 | ||
图片预览






文档简介
6.3.2 二项式系数的性质
新课程标准解读
核心素养
1.会用赋值法求展开式系数的和.
2.能记住二项式系数的性质,并能灵活运用性质解决相关问题.
1.数学抽象:二项式系数和问题.
2.数学运算:二项式系数的最大项问题.
复习引入
(a+b)n=
1、二项式定理
展开式中一共有n+1项.
2、二项展开式的通项
an-kbk
3、二项式的系数
Cn
0
Cn
1
Cn
k
Cn
n
…
…
二项式的系数的和
+ + + … + +… +=
Cn
0
Cn
1
Cn
2
Cn
k
Cn
n
2n
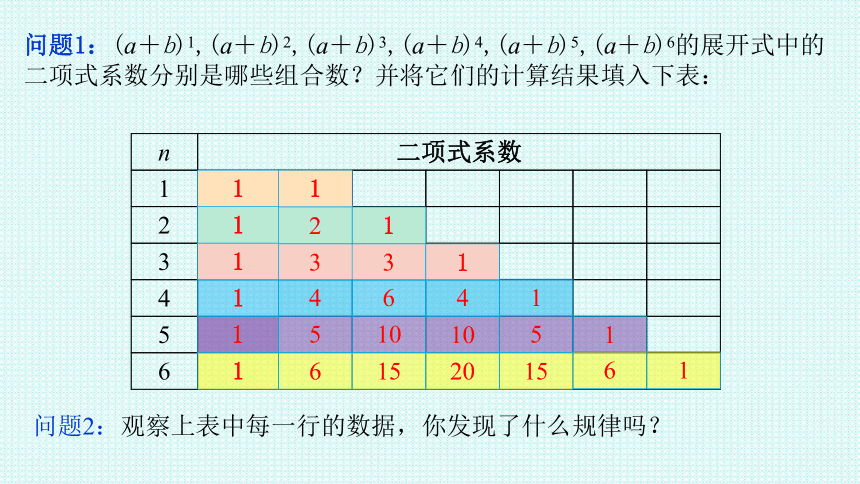
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
问题2:观察上表中每一行的数据,你发现了什么规律吗?
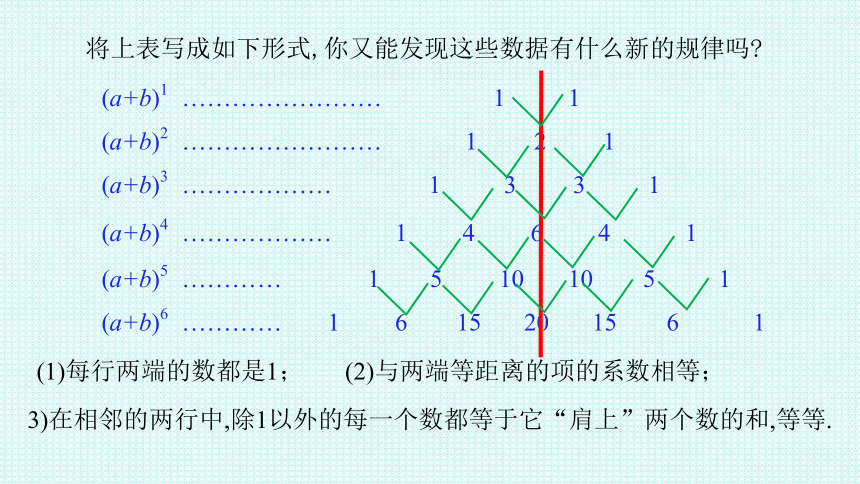
将上表写成如下形式,你又能发现这些数据有什么新的规律吗?
(a+b)1
……………………
1 1
(a+b)2
……………………
1 2 1
(a+b)3
………………
1 3 3 1
(a+b)4
………………
1
4
6
4
1
(a+b)5
…………
1 5 10 10 5 1
(a+b)6
…………
1
6
15
20
15
6
1
(1)每行两端的数都是1;
(2)与两端等距离的项的系数相等;
3)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
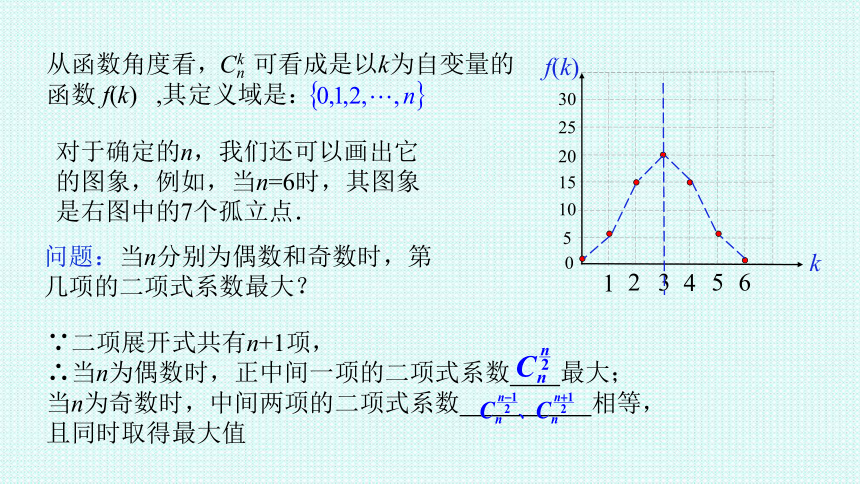
从函数角度看, 可看成是以k为自变量的函数 f(k) ,其定义域是:
Cn
k
对于确定的n,我们还可以画出它
的图象,例如,当n=6时,其图象
是右图中的7个孤立点.
0
5
10
15
20
25
30
f(k)
k
6
5
4
3
2
1
问题:当n分别为偶数和奇数时,第几项的二项式系数最大?
∵二项展开式共有n+1项,
∴当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,
且同时取得最大值
性质1:对称性
与首末两端“等距离”的两个二项式系数相等.
可直接由公式 得到.
Cn =
m
Cn
n-m
性质2:增减性与最大值
Cn=
k
n(n-1)(n-2)…(n-k+1)
k!
=
n(n-1)(n-2)…(n-k+2)(n-k+1)
k(k-1)!
=
Cn
k-1
k
n-k+1
若
?1,
k
n-k+1
k?
2
n+1
所以,当 时,
k?
2
n+1
二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,即先增后减,所以在中间项取得最大值。
性质3:各二项式系数的和
+ + + … + +… +=
Cn
0
Cn
1
Cn
2
Cn
k
Cn
n
2n
(a+b)n=
(赋值法)令a=1,b=1,则
同时由于 ,上式还可以写成:
Cn =1
0
+ + … + +… += -1
Cn
1
Cn
2
Cn
k
Cn
n
2n
例1 求证:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
(a+b)n=
an+ + +
an-1b
…
an-kbk
…
bn
Cn
0
Cn
1
Cn
k
Cn
n
奇数项的二项式系数的和
偶数项的二项式系数的和
Cn+
0
Cn+
2
Cn+
4
…
Cn+
1
Cn+
3
Cn+
5
…
∴不妨令a=1,b=-1,则可得
…
(1-1)n=
Cn-
0
Cn+
1
Cn-
2
Cn+
3
+(-1)n
Cn
n
( )
-( )=0
Cn+
0
Cn+
2
Cn+
4
…
Cn+
1
Cn+
3
Cn+
5
…
Cn+
0
Cn+
2
Cn+
4
…
Cn+
1
Cn+
3
Cn+
5
…
=
∴在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和
都等于2n-1
题型一 二项式系数和与各项的系数和的基本问题
的展开式中,所有二项式系数的和是32,则展开式中
各项系数的和为( )
A.-32 B.0 C.32 D.1
由题意知2n=32,得n=5.令x=1,可得展开式中各项系数的和为(3×12-1)5=32.
2.(2021·安徽省蚌埠市高三质检)在
除常数项外,
其余各项系数的和为( )
A.63 B.-517 C.-217 D.-177
581,
令x=1求各项系数和为(1+2-1)6=64,
64-581=-517.
(1)当x=1时,等号左边为(1-2)7=-1,等号右边为a0+a1+a2+…+a7,∴a0+a1+a2+…+a7=-1.当x=0时,a0=1.
∴a1+a2+…+a7=-1-1=-2.
(2)令x=1,得a0+a1+a2+…+a7=-1,①
令x=-1,得a0-a1+a2-a3+a4-a5+a6-a7=37,②
①-②,得2(a1+a3+a5+a7)=-1-37,
(3)由展开式,知a1,a3,a5,a7均为负数,a0,a2,a4,a6均为正数,
∴|a0|+|a1|+…+|a7|=a0-a1+a2-a3+a4-a5+a6-a7.
由(2)可知,a0-a1+a2-a3+a4-a5+a6-a7=37,
∴|a0|+|a1|+…+|a7|=37=2 187.
对于(a+bx)n=a0+a1x+a2x2+…+anxn的展开式,求各项系数和时,可令x=1,得a0+a1+a2+…+an=(a+b)n.
若求奇数项和或偶数项和,可分别令x=1和x=-1,
两式相加减即可求出结果.对于形如(ax2+bx+c)n的式子,求其展开式的各项系数和,只需令x=1.对于(ax+by)n(a,b为常数)的式子,求其展开式的各项系数和,可令x=y=1.
多项式x3+x10=a0+a1(x+1)+…+a9(x+1)9+a10(x+1)10.
(1)求a0+a1+…+a9+a10的值;
(2)求a0-a1+a2-a3+…-a9+a10的值;
(3)求a0.
(1)令x+1=1,即x=0,得0=a0+a1×1+…+a9×19+a10×110,
即a0+a1+…+a9+a10=0.
(2)令x+1=-1,即x=-2,得(-2)3+(-2)10=a0-a1+a2-a3+…-a9+a10,即a0-a1+a2-a3+…-a9+a10=1 016.
(3)令x+1=0,即x=-1,得a0=0.
题型二 系数最大项问题
例2 设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=( )
A.5 B.6 C.7 D.8
根据二项式系数的性质,知(x+y)2m的展开式中二项式系数的最大值为
而(x+y)2m+1的展开式中二项式系数的最大值为
解得m=6.
的展开式前三项的二项式系数的和等于37,
所以展开式中第5项的二项式系数最大,
(2)设二项展开式的第r+1项的系数最大,则
解得7≤r≤8,所以展开式中系数最大的项为第8项或第9项,即T8=
(2021·春季高考上海卷)已知(1+x)n的展开式中,唯有x3的系数最大,则(1+x)n的系数和为________.
则
解得5<n<7,又n∈N,因此n=6.
设(1+x)6=a0x6+a1x5+a2x4+…+a5x+a6,令x=1,则(1+x)6的系数和为a0+a1+a2+…+a6=26=64.
题型三 关于整除或余数问题
(1)证明:32n+3-24n+37能被64整除.
(2)求9192被100除所得的余数.
(1)32n+3-24n+37=3×9n+1-24n+37=3(8+1)n+1-24n+37
显然上式是64的倍数,故原式能被64整除.
因为展开式中前92项均能被100整除,所以只需求最后一项除以100的余数.
前91项均能被100整除,后两项和为-919.因余数为正,可从前面的数中分离出1 000,结果为1 000-919=81,故9192被100除所得的余数为81.
整除或求余数问题的求解策略
(1)用二项式定理处理整除问题,通常把幂的底数写成除数(或与除数密切关联的数)与某数的和或差的形式,再利用二项式定理展开,只考虑后面一、二项(或者是某些项)就可以了.
(2)要注意余数的范围,对给定的整数a,b(b≠0),有确定的一对整数q和r,满足a=bq+r,其中b为除数,r为余数,r∈[0,|b|),利用二项式定理展开变形后,若剩余部分是负数,要注意转换成正数.
1.211除以9的余数为________.
2.今天是星期四,那么8100天后的这一天是星期几?
8100=(7+1)100=
C100
1
798
C100
99
C100
0
799
+ +…+ +…+
C100
k
7100-k
=7( )+1
C100
1
799
C100
99
71
C100
0
7100
C100
100
+ +…+ +…+ +
C100
k
7100-k
余数是1,所以是星期五
课堂小结
(1)二项式系数的三个性质
与首末两端“等距离”的两个二项式系数相等
先增后减,在中间项取得最大值。
(2) 数学思想:函数思想
a 单调性;
b 图象;
c 最值
新课程标准解读
核心素养
1.会用赋值法求展开式系数的和.
2.能记住二项式系数的性质,并能灵活运用性质解决相关问题.
1.数学抽象:二项式系数和问题.
2.数学运算:二项式系数的最大项问题.
复习引入
(a+b)n=
1、二项式定理
展开式中一共有n+1项.
2、二项展开式的通项
an-kbk
3、二项式的系数
Cn
0
Cn
1
Cn
k
Cn
n
…
…
二项式的系数的和
+ + + … + +… +=
Cn
0
Cn
1
Cn
2
Cn
k
Cn
n
2n
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
问题2:观察上表中每一行的数据,你发现了什么规律吗?
将上表写成如下形式,你又能发现这些数据有什么新的规律吗?
(a+b)1
……………………
1 1
(a+b)2
……………………
1 2 1
(a+b)3
………………
1 3 3 1
(a+b)4
………………
1
4
6
4
1
(a+b)5
…………
1 5 10 10 5 1
(a+b)6
…………
1
6
15
20
15
6
1
(1)每行两端的数都是1;
(2)与两端等距离的项的系数相等;
3)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
从函数角度看, 可看成是以k为自变量的函数 f(k) ,其定义域是:
Cn
k
对于确定的n,我们还可以画出它
的图象,例如,当n=6时,其图象
是右图中的7个孤立点.
0
5
10
15
20
25
30
f(k)
k
6
5
4
3
2
1
问题:当n分别为偶数和奇数时,第几项的二项式系数最大?
∵二项展开式共有n+1项,
∴当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,
且同时取得最大值
性质1:对称性
与首末两端“等距离”的两个二项式系数相等.
可直接由公式 得到.
Cn =
m
Cn
n-m
性质2:增减性与最大值
Cn=
k
n(n-1)(n-2)…(n-k+1)
k!
=
n(n-1)(n-2)…(n-k+2)(n-k+1)
k(k-1)!
=
Cn
k-1
k
n-k+1
若
?1,
k
n-k+1
k?
2
n+1
所以,当 时,
k?
2
n+1
二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,即先增后减,所以在中间项取得最大值。
性质3:各二项式系数的和
+ + + … + +… +=
Cn
0
Cn
1
Cn
2
Cn
k
Cn
n
2n
(a+b)n=
(赋值法)令a=1,b=1,则
同时由于 ,上式还可以写成:
Cn =1
0
+ + … + +… += -1
Cn
1
Cn
2
Cn
k
Cn
n
2n
例1 求证:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
(a+b)n=
an+ + +
an-1b
…
an-kbk
…
bn
Cn
0
Cn
1
Cn
k
Cn
n
奇数项的二项式系数的和
偶数项的二项式系数的和
Cn+
0
Cn+
2
Cn+
4
…
Cn+
1
Cn+
3
Cn+
5
…
∴不妨令a=1,b=-1,则可得
…
(1-1)n=
Cn-
0
Cn+
1
Cn-
2
Cn+
3
+(-1)n
Cn
n
( )
-( )=0
Cn+
0
Cn+
2
Cn+
4
…
Cn+
1
Cn+
3
Cn+
5
…
Cn+
0
Cn+
2
Cn+
4
…
Cn+
1
Cn+
3
Cn+
5
…
=
∴在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和
都等于2n-1
题型一 二项式系数和与各项的系数和的基本问题
的展开式中,所有二项式系数的和是32,则展开式中
各项系数的和为( )
A.-32 B.0 C.32 D.1
由题意知2n=32,得n=5.令x=1,可得展开式中各项系数的和为(3×12-1)5=32.
2.(2021·安徽省蚌埠市高三质检)在
除常数项外,
其余各项系数的和为( )
A.63 B.-517 C.-217 D.-177
581,
令x=1求各项系数和为(1+2-1)6=64,
64-581=-517.
(1)当x=1时,等号左边为(1-2)7=-1,等号右边为a0+a1+a2+…+a7,∴a0+a1+a2+…+a7=-1.当x=0时,a0=1.
∴a1+a2+…+a7=-1-1=-2.
(2)令x=1,得a0+a1+a2+…+a7=-1,①
令x=-1,得a0-a1+a2-a3+a4-a5+a6-a7=37,②
①-②,得2(a1+a3+a5+a7)=-1-37,
(3)由展开式,知a1,a3,a5,a7均为负数,a0,a2,a4,a6均为正数,
∴|a0|+|a1|+…+|a7|=a0-a1+a2-a3+a4-a5+a6-a7.
由(2)可知,a0-a1+a2-a3+a4-a5+a6-a7=37,
∴|a0|+|a1|+…+|a7|=37=2 187.
对于(a+bx)n=a0+a1x+a2x2+…+anxn的展开式,求各项系数和时,可令x=1,得a0+a1+a2+…+an=(a+b)n.
若求奇数项和或偶数项和,可分别令x=1和x=-1,
两式相加减即可求出结果.对于形如(ax2+bx+c)n的式子,求其展开式的各项系数和,只需令x=1.对于(ax+by)n(a,b为常数)的式子,求其展开式的各项系数和,可令x=y=1.
多项式x3+x10=a0+a1(x+1)+…+a9(x+1)9+a10(x+1)10.
(1)求a0+a1+…+a9+a10的值;
(2)求a0-a1+a2-a3+…-a9+a10的值;
(3)求a0.
(1)令x+1=1,即x=0,得0=a0+a1×1+…+a9×19+a10×110,
即a0+a1+…+a9+a10=0.
(2)令x+1=-1,即x=-2,得(-2)3+(-2)10=a0-a1+a2-a3+…-a9+a10,即a0-a1+a2-a3+…-a9+a10=1 016.
(3)令x+1=0,即x=-1,得a0=0.
题型二 系数最大项问题
例2 设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=( )
A.5 B.6 C.7 D.8
根据二项式系数的性质,知(x+y)2m的展开式中二项式系数的最大值为
而(x+y)2m+1的展开式中二项式系数的最大值为
解得m=6.
的展开式前三项的二项式系数的和等于37,
所以展开式中第5项的二项式系数最大,
(2)设二项展开式的第r+1项的系数最大,则
解得7≤r≤8,所以展开式中系数最大的项为第8项或第9项,即T8=
(2021·春季高考上海卷)已知(1+x)n的展开式中,唯有x3的系数最大,则(1+x)n的系数和为________.
则
解得5<n<7,又n∈N,因此n=6.
设(1+x)6=a0x6+a1x5+a2x4+…+a5x+a6,令x=1,则(1+x)6的系数和为a0+a1+a2+…+a6=26=64.
题型三 关于整除或余数问题
(1)证明:32n+3-24n+37能被64整除.
(2)求9192被100除所得的余数.
(1)32n+3-24n+37=3×9n+1-24n+37=3(8+1)n+1-24n+37
显然上式是64的倍数,故原式能被64整除.
因为展开式中前92项均能被100整除,所以只需求最后一项除以100的余数.
前91项均能被100整除,后两项和为-919.因余数为正,可从前面的数中分离出1 000,结果为1 000-919=81,故9192被100除所得的余数为81.
整除或求余数问题的求解策略
(1)用二项式定理处理整除问题,通常把幂的底数写成除数(或与除数密切关联的数)与某数的和或差的形式,再利用二项式定理展开,只考虑后面一、二项(或者是某些项)就可以了.
(2)要注意余数的范围,对给定的整数a,b(b≠0),有确定的一对整数q和r,满足a=bq+r,其中b为除数,r为余数,r∈[0,|b|),利用二项式定理展开变形后,若剩余部分是负数,要注意转换成正数.
1.211除以9的余数为________.
2.今天是星期四,那么8100天后的这一天是星期几?
8100=(7+1)100=
C100
1
798
C100
99
C100
0
799
+ +…+ +…+
C100
k
7100-k
=7( )+1
C100
1
799
C100
99
71
C100
0
7100
C100
100
+ +…+ +…+ +
C100
k
7100-k
余数是1,所以是星期五
课堂小结
(1)二项式系数的三个性质
与首末两端“等距离”的两个二项式系数相等
先增后减,在中间项取得最大值。
(2) 数学思想:函数思想
a 单调性;
b 图象;
c 最值
