人教A版(2019)选择性必修第三册7.3.2离散型随机变量的方差 课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册7.3.2离散型随机变量的方差 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 20:45:00 | ||
图片预览






文档简介
(共24张PPT)
7.3.2离散型随机变量的方差
新课程标准解读 核心素养
1.理解并会计算离散型随机变量的方差. 2.能利用方差的意义分析解决实际问题. 1.数学抽象、数学运算:方差的理解和计算.
2.数学建模:方差的实际应用.
温故知新
1.离散型随机变量的均值
E(X)=x1p1+x2p2+…+xnpn=
Σx ipi
n
i=1
2.离散型随机变量均值的运算性质
E(aX+b)=aE(X)+b
随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小.所以我们还需要寻找反映随机变量取值波动大小的数字特征.
情景引例
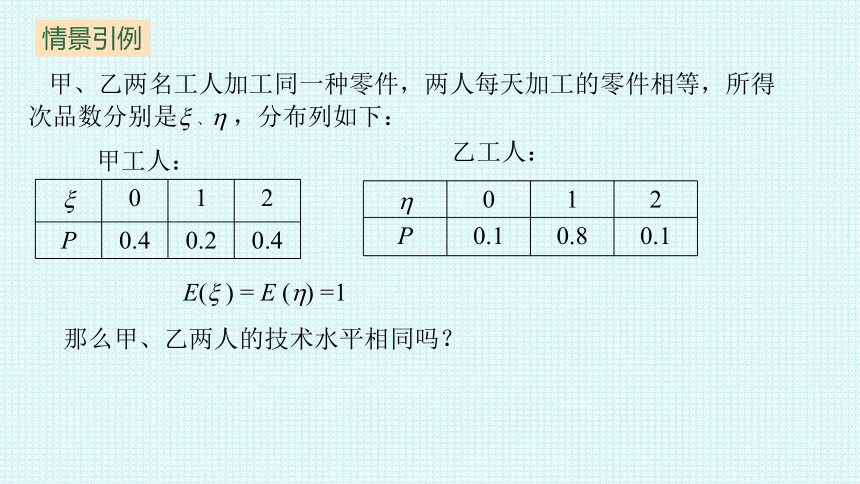
甲、乙两名工人加工同一种零件,两人每天加工的零件相等,所得次品数分别是 、 ,分布列如下:
0 1 2
P 0.4 0.2 0.4
0 1 2
P 0.1 0.8 0.1
甲工人:
乙工人:
E( ) = E ( ) =1
那么甲、乙两人的技术水平相同吗?
从两名运动员中挑出一名参加射击比赛。根据以往的成绩记录,甲、乙两名运动员击中目标靶的环数X和Y的分布列如下表1和表2所示:
X 6 7 8 9 10
P 0.09 0.24 0.32 0.28 0.07
Y 6 7 8 9 10
P 0.07 0.22 0.38 0.3 0.03
E(X)= 8 ;E(Y)=8
因为两个均值相等,所以均值不能区分这两名运动员的射击水平。
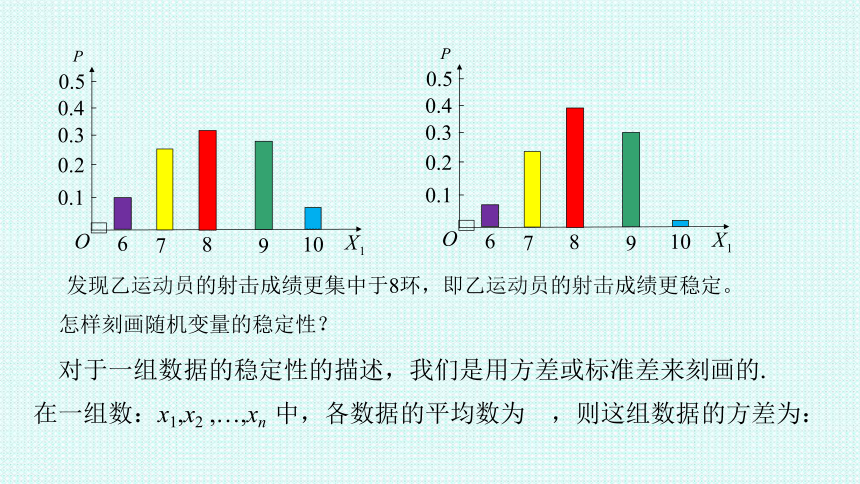
射击水平除了要考虑击中环数的均值外,还要考虑稳定性,即击中环数的离散程度,图一和图二分别是X和Y的概率分布图:
O
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
O
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
发现乙运动员的射击成绩更集中于8环,即乙运动员的射击成绩更稳定。
怎样刻画随机变量的稳定性?
对于一组数据的稳定性的描述,我们是用方差或标准差来刻画的.
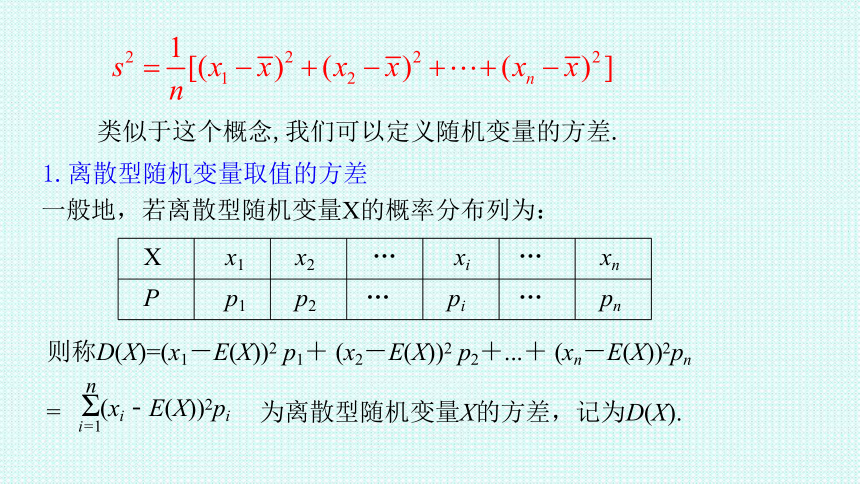
在一组数:x1,x2 ,…,xn 中,各数据的平均数为 ,则这组数据的方差为:
类似于这个概念,我们可以定义随机变量的方差.
1.离散型随机变量取值的方差
一般地,若离散型随机变量X的概率分布列为:
X x1 x2 … xi … xn
P p1 p2 … pi … pn
则称D(X)=(x1-E(X))2 p1+ (x2-E(X))2 p2+...+ (xn-E(X))2pn
=
Σ(xi-E(X))2pi
n
i=1
为离散型随机变量X的方差,记为D(X).
其算术平方根为X的标准差: 记为
它们都是反映离散型随机变量偏离于均值的平均程度的量,它们的值越小,则随机变量偏离于均值的平均程度越小,即越集中于均值。
随机变量的方差和标准差都可以度量随机变量的取值与其均值的偏离程度,反映了随机变量取值的离散程度,方差或标准差越小,随机变量的取值越集中;方差或标准差越大,随机变量的取值越分散。
两名同学射击成绩的方差和标准差分别为:
所以随机变量Y的取值相对更集中,即乙同学的射击成绩相对更稳定。
1.已知X的分布列如下:
X 1 2 3 4
P
E(X)=1 × +2× +3× +4× =
D(X)=(1- )2× +(1- )2 × +(1- )2× +(1- )2× =
2.(2021·工农区校级期末)已知随机变量X的分布列如下:
X 0 1
P p 1-p
则p的值为( )
由随机变量X的分布列,知E(X)=1-p,
所以D(X)=(p-1)2·p+
2.方差的性质
(1)D(X+b)=_______;
(2)D(aX)=_______;
(3)D(aX+b)=______________.
D(X)
a2D(X)
a2D(X)
平移变化不改变方差,但是伸缩变化改变方差
方差的几个恒等变形
探究点1 求离散型随机变量的方差
例1已知X的分布列为
X -1 0 1
P a
(1)求X2的分布列;
(2)计算X的方差;
(3)若Y=4X+3,求Y的均值和方差.
(1)由分布列的性质,
从而X2的分布列为
X2 0 1
P
所以X的均值E(X)=
故X的方差D(X)=
所以X的均值E(X)=
所以X的方差D(X)=E(X2)-[E(X)]2
(3)因为Y=4X+3,所以E(Y)=4E(X)+3=2,D(Y)=42D(X)=11.
求离散型随机变量的方差的步骤
(1)明确随机变量的取值,并求出随机变量取各个值的概率.
(2)写出分布列.
(3)利用公式E(X)=x1p1+x2p2+…+xnpn求出随机变量的期望E(X).
(4)代入公式D(X)=(x1-E(X))2p1+(x2-E(X))2p2+…+(xi-E(X))2·pi+…+(xn-E(X))2pn求出方差D(X).
1.(2021·浙江杭州第四中学高三期中)设0X 0 a 1
P
所以4a2-4a+4=3,即(2a-1)2=0,
2.(2021·江西宜春高二期末)随机变量X的分布列如下:
X 0 1
P 0.2 m
已知随机变量Y=aX+b(a,b∈R),且E(Y)=10,D(Y)=4,则a与b的值为( )
A.a=10,b=3 B.a=3,b=10
C.a=5,b=6 D.a=6,b=5
因为0.2+m=1,所以m=0.8,
所以E(X)=0×0.2+1×0.8=0.8,D(X)=0.2×0.8=0.16.
因为E(Y)=10,D(Y)=4,
所以aE(X)+b=0.8a+b=10,a2D(X)=0.16a2=4,
解得a=5,b=6
探究点2 方差在决策问题的应用
(1)求a,b,c的值;
(2)若将100万元全部投到其中一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
设投到项目A,B的资金都为x万元,变量X1和X2分别表示投资项目A和B所获得的利润,则X1和X2的分布列分别为
X1 0.4x -0.2x 0
P
X2 0.3x -0.1x
P b c
由分布列得E(X1)=0.4x
=0.2x,
E(X2)=0.3bx-0.1cx,因为E(X1)=E(X2),所以0.3bx-0.1cx=0.2x,
即0.3b-0.1c=0.2.
又b+c=1,
(2)选择项目B.理由如下:
当投入100万元资金时,由(1)知x=100,所以E(X1)=E(X2)=20,
=600,
因为E(X1)=E(X2),D(X1)>D(X2)说明虽然项目A和项目B的平均收益相等,但项目B更稳妥,所以从投资回报稳定性的角度考虑,建议该投资公司选择项目B.
利用均值和方差解决实际问题的步骤
(1)比较均值:离散型随机变量的均值反映了离散型随机变量取值的平均水平,因此,在实际决策问题中,需先计算均值,看一下谁的平均水平高.
(2)在均值相等的情况下计算方差:方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度.通过计算方差,分析一下谁的水平发挥相对稳定.
(3)下结论:依据均值和方差的几何意义做出结论.
例3 有甲、乙两个建材厂,都想投标参加某重点工程,为了对重点工程负责,政府到两建材厂抽样检查,从中各取等量的样品检查它们的抗拉强度,抗拉强度的分布列分别如下:
ξ 110 120 125 130 135
P 0.1 0.2 0.4 0.1 0.2
η 100 115 125 130 145
P 0.1 0.2 0.4 0.1 0.2
其中ξ和η分别表示甲、乙建材厂材料的抗拉强度,在使用时要求抗拉强度不低于120,那么哪个建材厂的材料稳定性较好?
E(ξ)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(η)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(ξ)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
D(η)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165,
由于E(ξ)=E(η)而D(ξ)1.已知随机变量ξ的分布列如下表,且E(ξ)=1.1,则D(ξ)=( )
A.0.36 B.0.52 C.0.49 D.0.68
先由随机变量分布列的性质解得
1.1,得x=2,
=0.49.
2.(2021·浙江模拟)已知随机变量X的分布列如表:
则当a在(0,1)内增大时,( )
A.D(X)减小 B.D(X)增大
C.D(X)先减小后增大 D.D(X)先增大后减小
所以当a在(0,1)内增大时,D(X)减小.
课堂小结
1.已知随机变量的概率分布,求它的均值、方差(或标准差),可直接由定义(公式)求解.
2.对于一般的离散型随机变量ξ求方差、标准差可采用如下步骤:
(1)理解ξ的意义,写出ξ可能取的全部值.
(2)求ξ取各个值的概率,写出分布列.
(3)根据分布列,由数学期望的定义求出E(ξ).
(4)根据方差、标准差的定义求出D(ξ),
7.3.2离散型随机变量的方差
新课程标准解读 核心素养
1.理解并会计算离散型随机变量的方差. 2.能利用方差的意义分析解决实际问题. 1.数学抽象、数学运算:方差的理解和计算.
2.数学建模:方差的实际应用.
温故知新
1.离散型随机变量的均值
E(X)=x1p1+x2p2+…+xnpn=
Σx ipi
n
i=1
2.离散型随机变量均值的运算性质
E(aX+b)=aE(X)+b
随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小.所以我们还需要寻找反映随机变量取值波动大小的数字特征.
情景引例
甲、乙两名工人加工同一种零件,两人每天加工的零件相等,所得次品数分别是 、 ,分布列如下:
0 1 2
P 0.4 0.2 0.4
0 1 2
P 0.1 0.8 0.1
甲工人:
乙工人:
E( ) = E ( ) =1
那么甲、乙两人的技术水平相同吗?
从两名运动员中挑出一名参加射击比赛。根据以往的成绩记录,甲、乙两名运动员击中目标靶的环数X和Y的分布列如下表1和表2所示:
X 6 7 8 9 10
P 0.09 0.24 0.32 0.28 0.07
Y 6 7 8 9 10
P 0.07 0.22 0.38 0.3 0.03
E(X)= 8 ;E(Y)=8
因为两个均值相等,所以均值不能区分这两名运动员的射击水平。
射击水平除了要考虑击中环数的均值外,还要考虑稳定性,即击中环数的离散程度,图一和图二分别是X和Y的概率分布图:
O
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
O
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
发现乙运动员的射击成绩更集中于8环,即乙运动员的射击成绩更稳定。
怎样刻画随机变量的稳定性?
对于一组数据的稳定性的描述,我们是用方差或标准差来刻画的.
在一组数:x1,x2 ,…,xn 中,各数据的平均数为 ,则这组数据的方差为:
类似于这个概念,我们可以定义随机变量的方差.
1.离散型随机变量取值的方差
一般地,若离散型随机变量X的概率分布列为:
X x1 x2 … xi … xn
P p1 p2 … pi … pn
则称D(X)=(x1-E(X))2 p1+ (x2-E(X))2 p2+...+ (xn-E(X))2pn
=
Σ(xi-E(X))2pi
n
i=1
为离散型随机变量X的方差,记为D(X).
其算术平方根为X的标准差: 记为
它们都是反映离散型随机变量偏离于均值的平均程度的量,它们的值越小,则随机变量偏离于均值的平均程度越小,即越集中于均值。
随机变量的方差和标准差都可以度量随机变量的取值与其均值的偏离程度,反映了随机变量取值的离散程度,方差或标准差越小,随机变量的取值越集中;方差或标准差越大,随机变量的取值越分散。
两名同学射击成绩的方差和标准差分别为:
所以随机变量Y的取值相对更集中,即乙同学的射击成绩相对更稳定。
1.已知X的分布列如下:
X 1 2 3 4
P
E(X)=1 × +2× +3× +4× =
D(X)=(1- )2× +(1- )2 × +(1- )2× +(1- )2× =
2.(2021·工农区校级期末)已知随机变量X的分布列如下:
X 0 1
P p 1-p
则p的值为( )
由随机变量X的分布列,知E(X)=1-p,
所以D(X)=(p-1)2·p+
2.方差的性质
(1)D(X+b)=_______;
(2)D(aX)=_______;
(3)D(aX+b)=______________.
D(X)
a2D(X)
a2D(X)
平移变化不改变方差,但是伸缩变化改变方差
方差的几个恒等变形
探究点1 求离散型随机变量的方差
例1已知X的分布列为
X -1 0 1
P a
(1)求X2的分布列;
(2)计算X的方差;
(3)若Y=4X+3,求Y的均值和方差.
(1)由分布列的性质,
从而X2的分布列为
X2 0 1
P
所以X的均值E(X)=
故X的方差D(X)=
所以X的均值E(X)=
所以X的方差D(X)=E(X2)-[E(X)]2
(3)因为Y=4X+3,所以E(Y)=4E(X)+3=2,D(Y)=42D(X)=11.
求离散型随机变量的方差的步骤
(1)明确随机变量的取值,并求出随机变量取各个值的概率.
(2)写出分布列.
(3)利用公式E(X)=x1p1+x2p2+…+xnpn求出随机变量的期望E(X).
(4)代入公式D(X)=(x1-E(X))2p1+(x2-E(X))2p2+…+(xi-E(X))2·pi+…+(xn-E(X))2pn求出方差D(X).
1.(2021·浙江杭州第四中学高三期中)设0
P
所以4a2-4a+4=3,即(2a-1)2=0,
2.(2021·江西宜春高二期末)随机变量X的分布列如下:
X 0 1
P 0.2 m
已知随机变量Y=aX+b(a,b∈R),且E(Y)=10,D(Y)=4,则a与b的值为( )
A.a=10,b=3 B.a=3,b=10
C.a=5,b=6 D.a=6,b=5
因为0.2+m=1,所以m=0.8,
所以E(X)=0×0.2+1×0.8=0.8,D(X)=0.2×0.8=0.16.
因为E(Y)=10,D(Y)=4,
所以aE(X)+b=0.8a+b=10,a2D(X)=0.16a2=4,
解得a=5,b=6
探究点2 方差在决策问题的应用
(1)求a,b,c的值;
(2)若将100万元全部投到其中一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
设投到项目A,B的资金都为x万元,变量X1和X2分别表示投资项目A和B所获得的利润,则X1和X2的分布列分别为
X1 0.4x -0.2x 0
P
X2 0.3x -0.1x
P b c
由分布列得E(X1)=0.4x
=0.2x,
E(X2)=0.3bx-0.1cx,因为E(X1)=E(X2),所以0.3bx-0.1cx=0.2x,
即0.3b-0.1c=0.2.
又b+c=1,
(2)选择项目B.理由如下:
当投入100万元资金时,由(1)知x=100,所以E(X1)=E(X2)=20,
=600,
因为E(X1)=E(X2),D(X1)>D(X2)说明虽然项目A和项目B的平均收益相等,但项目B更稳妥,所以从投资回报稳定性的角度考虑,建议该投资公司选择项目B.
利用均值和方差解决实际问题的步骤
(1)比较均值:离散型随机变量的均值反映了离散型随机变量取值的平均水平,因此,在实际决策问题中,需先计算均值,看一下谁的平均水平高.
(2)在均值相等的情况下计算方差:方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度.通过计算方差,分析一下谁的水平发挥相对稳定.
(3)下结论:依据均值和方差的几何意义做出结论.
例3 有甲、乙两个建材厂,都想投标参加某重点工程,为了对重点工程负责,政府到两建材厂抽样检查,从中各取等量的样品检查它们的抗拉强度,抗拉强度的分布列分别如下:
ξ 110 120 125 130 135
P 0.1 0.2 0.4 0.1 0.2
η 100 115 125 130 145
P 0.1 0.2 0.4 0.1 0.2
其中ξ和η分别表示甲、乙建材厂材料的抗拉强度,在使用时要求抗拉强度不低于120,那么哪个建材厂的材料稳定性较好?
E(ξ)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(η)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(ξ)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
D(η)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165,
由于E(ξ)=E(η)而D(ξ)
A.0.36 B.0.52 C.0.49 D.0.68
先由随机变量分布列的性质解得
1.1,得x=2,
=0.49.
2.(2021·浙江模拟)已知随机变量X的分布列如表:
则当a在(0,1)内增大时,( )
A.D(X)减小 B.D(X)增大
C.D(X)先减小后增大 D.D(X)先增大后减小
所以当a在(0,1)内增大时,D(X)减小.
课堂小结
1.已知随机变量的概率分布,求它的均值、方差(或标准差),可直接由定义(公式)求解.
2.对于一般的离散型随机变量ξ求方差、标准差可采用如下步骤:
(1)理解ξ的意义,写出ξ可能取的全部值.
(2)求ξ取各个值的概率,写出分布列.
(3)根据分布列,由数学期望的定义求出E(ξ).
(4)根据方差、标准差的定义求出D(ξ),
