人教A版(2019)选择性必修第二册5.1.1变化率问题 课件(共16张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册5.1.1变化率问题 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 20:49:26 | ||
图片预览





文档简介
5.1.1变化率问题
新课程标准解读
核心素养
1.通过对大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程.
2.会求函数在某一点附近的平均变化率.
3.理解函数的平均变化率,瞬时变化率及瞬时速度的概念.
1.通过对函数的平均变化率、瞬时变化率、瞬时速度的概念的学习,培养数学抽象的核心素养.
2.通过求平均变化率、瞬时变化率及瞬时速度的学习,培养逻辑推理及数学运算的核心素养.
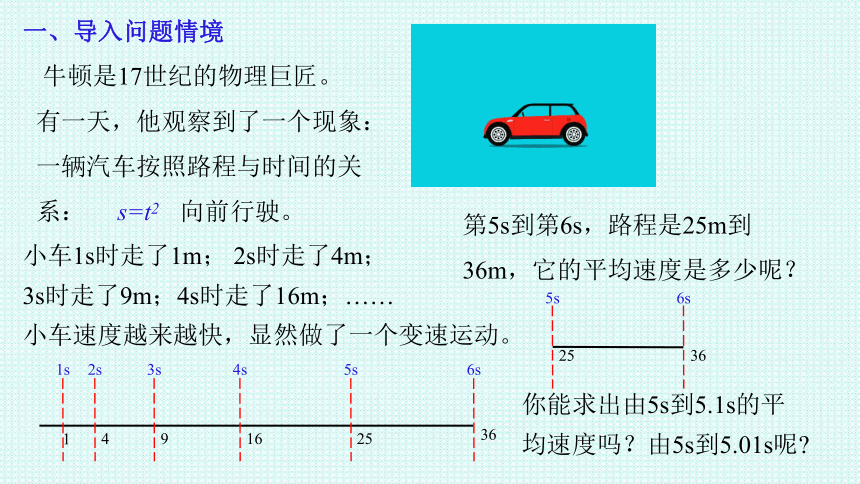
牛顿是17世纪的物理巨匠。 有一天,他观察到了一个现象:一辆汽车按照路程与时间的关系: s=t2 向前行驶。
小车1s时走了1m; 2s时走了4m;
3s时走了9m;4s时走了16m;……
小车速度越来越快,显然做了一个变速运动。
4s
1s
2s
3s
5s
6s
1
4
9
16
25
36
第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
一、导入问题情境
5s
6s
25
36
你能求出由5s到5.1s的平均速度吗?由5s到5.01s呢?
1.平均变化率:
二、新知探究
一般地,函数f(x)在区间 [x1 , x2] 上的平均变化率为
注意:(1)平均变化率不能脱离区间而言,不同区间上平均变化率可能不同.
(2)若设?x=x2-x1,?y=y2-y1,则函数f(x)在区间[x1,x2]上的平均变化率可写为 .平均变化率的实质就是 .
函数值的改变量与自变量的改变量之比
1、式子中△x 、△ y 的值可正、可负,但 的△x值不能为0, △ y 的值可以为0
?y
?x
2、若函数f (x)为常函数时, △ y =0
3、变式:
例1 已知一物体的运动方程为s(t)=t2+2t+3,求该物体在t=1到t=1+Δt这段时间内的平均速度.
物体在t=1到t=1+Δt这段时间内的位移增量
Δs=s(1+Δt)-s(1)
=[(1+Δt)2+2(1+Δt)+3]-(12+2×1+3)
=(Δt)2+4Δt.
物体在t=1到t=1+Δt这段时间内的平均速度为
=4+Δt.
Δt是时间改变量,可以是正值,也可以是负值,但不为0.当Δt >0时,1 +Δt在1之后;当Δt<0时,1 +Δt在1之前.
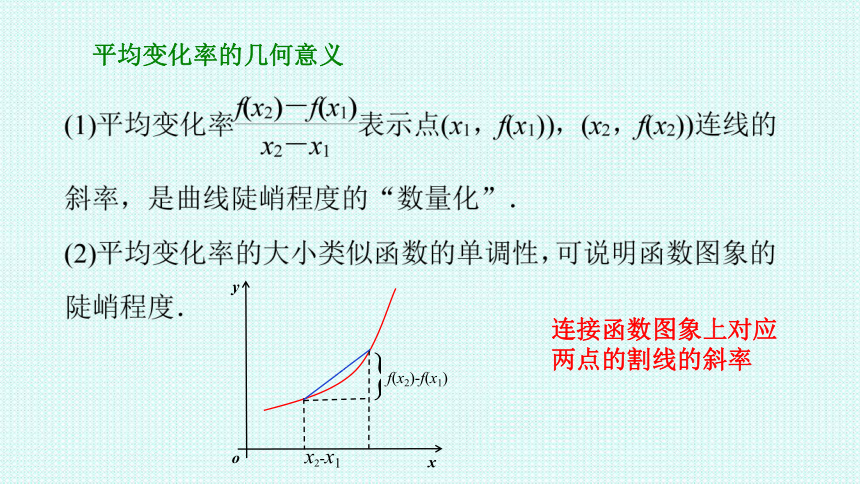
平均变化率的几何意义
x
y
o
x2-x1
f(x2)-f(x1)
连接函数图象上对应两点的割线的斜率
在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
如果用运动员在某段时间内的平均速度V
描述其运动状态,那么:
(1)在0?t?0.5 这段时间里,
(2)在1?t?2 这段时间里,
计算运动员在 这段时间里的平均速度,并思考以下问题:
(1)运动员在这段时间是静止的吗?
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
平均速度不能准确反映该段时间的运动状态.
2.瞬时变化率:
瞬时速度
(1)物体在 的速度称为瞬时速度.
某一时刻
一般地,设物体的运动规律是s=s(t),则物体在t0到t0+Δt这段时间内的平均速度为
如果Δt无限趋近于0时,
无限趋近于某个常数v,我们就说当Δt趋近于0时,
这时v就是物体在时刻t=t0时的瞬时速度,即瞬时速度v=
( )
( )
( )
( )
极限
瞬时变化率
(2)函数f (x)在x=x0处的瞬时变化率是函数f (x)从x0到x0+Δx的平均变化率在Δx→0时的极限,
对函数在x0处的瞬时变化率的理解
(3)瞬时变化率刻画的是函数在某一点处变化的快慢,物体在某一时刻的瞬时速度是函数瞬时变化率的物理意义.
(4)函数在x0处的瞬时变化率仅与x0有关,而与Δx无关.
(1)在 ,Δx可正,可负,但不可为0.但Δy可以为0,此时f(x)为常数函数.
(2)在 中,当Δx趋向于0时, 也趋于一个定值.
例2 如果某物体的运动路程s与时间t满足函数s=2(1+t2)(s的单位为m,t的单位为s),求此物体在1.2 s末的瞬时速度.
Δs=2[1+(1.2+Δt)2]-2(1+1.22)=4.8Δt+2(Δt)2,
故物体在1.2 s末的瞬时速度为4.8 m/s.
①在极限表达式中,可把Δx作为一个数来参与运算.
②求出 的表达式后,Δx无限趋近于0,可令Δx=0,求出结果即可.
一做直线运动的物体,其位移s与时间t的关系是s(t)=3t-t2.
(1)求此物体的初速度;
(2)求此物体在t=2时的瞬时速度.
(1)t=0时的速度为初速度.在0时刻取一时间段[0,0+Δt],即[0,Δt],所以Δs=s(Δt)-s(0)=[3Δt-(Δt)2]-(3×0-02)
=3Δt-(Δt)2,
所以物体的初速度为3.
(2)取一时间段[2,2+Δt],所以Δs=s(2+Δt)-s(2)
=[3(2+Δt)-(2+Δt)2]-(3×2-22)=-Δt-(Δt)2,
( )
抛物线的切线的斜率
当点P无限趋近于P0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为抛物线f(x)在点P0处的切线,我们可以用割线P0P的斜率k近似地表示切线P0T的斜率k0.
x
y
o
P0
P
例3 求抛物线y=2x2+4x在点(3,30)处的切线方程.
Δy=2(3+Δx)2+4(3+Δx)-(2×32+4×3)
=12Δx+2(Δx)2+4Δx=2(Δx)2+16Δx
∴在点(3,30)处的切线方程为:y-30=16(x-3)即:16x-y-18=0.
求抛物线y=x2+3在点(2,7)处的切线方程.
Δy=[(2+Δx)2+3]-(22+3)=4Δx+(Δx)2
∴在点(2,7)处的切线方程为:y-7=4(x-2)
即:4x-y-1=0.
课时总结
1.平均速度只能粗略地反映物体在一段时间内里的运动状态,并不代表物体在每时每刻的运动情况,但是它是求瞬时速度的基础,瞬时速度是平均速度当Δt→0时的极限值.
2.函数y=f (x)在x=x0处的切线斜率反映了函数在该点处的瞬时变化率,它揭示了事物在某时刻的变化情况.
新课程标准解读
核心素养
1.通过对大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程.
2.会求函数在某一点附近的平均变化率.
3.理解函数的平均变化率,瞬时变化率及瞬时速度的概念.
1.通过对函数的平均变化率、瞬时变化率、瞬时速度的概念的学习,培养数学抽象的核心素养.
2.通过求平均变化率、瞬时变化率及瞬时速度的学习,培养逻辑推理及数学运算的核心素养.
牛顿是17世纪的物理巨匠。 有一天,他观察到了一个现象:一辆汽车按照路程与时间的关系: s=t2 向前行驶。
小车1s时走了1m; 2s时走了4m;
3s时走了9m;4s时走了16m;……
小车速度越来越快,显然做了一个变速运动。
4s
1s
2s
3s
5s
6s
1
4
9
16
25
36
第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
一、导入问题情境
5s
6s
25
36
你能求出由5s到5.1s的平均速度吗?由5s到5.01s呢?
1.平均变化率:
二、新知探究
一般地,函数f(x)在区间 [x1 , x2] 上的平均变化率为
注意:(1)平均变化率不能脱离区间而言,不同区间上平均变化率可能不同.
(2)若设?x=x2-x1,?y=y2-y1,则函数f(x)在区间[x1,x2]上的平均变化率可写为 .平均变化率的实质就是 .
函数值的改变量与自变量的改变量之比
1、式子中△x 、△ y 的值可正、可负,但 的△x值不能为0, △ y 的值可以为0
?y
?x
2、若函数f (x)为常函数时, △ y =0
3、变式:
例1 已知一物体的运动方程为s(t)=t2+2t+3,求该物体在t=1到t=1+Δt这段时间内的平均速度.
物体在t=1到t=1+Δt这段时间内的位移增量
Δs=s(1+Δt)-s(1)
=[(1+Δt)2+2(1+Δt)+3]-(12+2×1+3)
=(Δt)2+4Δt.
物体在t=1到t=1+Δt这段时间内的平均速度为
=4+Δt.
Δt是时间改变量,可以是正值,也可以是负值,但不为0.当Δt >0时,1 +Δt在1之后;当Δt<0时,1 +Δt在1之前.
平均变化率的几何意义
x
y
o
x2-x1
f(x2)-f(x1)
连接函数图象上对应两点的割线的斜率
在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
如果用运动员在某段时间内的平均速度V
描述其运动状态,那么:
(1)在0?t?0.5 这段时间里,
(2)在1?t?2 这段时间里,
计算运动员在 这段时间里的平均速度,并思考以下问题:
(1)运动员在这段时间是静止的吗?
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
平均速度不能准确反映该段时间的运动状态.
2.瞬时变化率:
瞬时速度
(1)物体在 的速度称为瞬时速度.
某一时刻
一般地,设物体的运动规律是s=s(t),则物体在t0到t0+Δt这段时间内的平均速度为
如果Δt无限趋近于0时,
无限趋近于某个常数v,我们就说当Δt趋近于0时,
这时v就是物体在时刻t=t0时的瞬时速度,即瞬时速度v=
( )
( )
( )
( )
极限
瞬时变化率
(2)函数f (x)在x=x0处的瞬时变化率是函数f (x)从x0到x0+Δx的平均变化率在Δx→0时的极限,
对函数在x0处的瞬时变化率的理解
(3)瞬时变化率刻画的是函数在某一点处变化的快慢,物体在某一时刻的瞬时速度是函数瞬时变化率的物理意义.
(4)函数在x0处的瞬时变化率仅与x0有关,而与Δx无关.
(1)在 ,Δx可正,可负,但不可为0.但Δy可以为0,此时f(x)为常数函数.
(2)在 中,当Δx趋向于0时, 也趋于一个定值.
例2 如果某物体的运动路程s与时间t满足函数s=2(1+t2)(s的单位为m,t的单位为s),求此物体在1.2 s末的瞬时速度.
Δs=2[1+(1.2+Δt)2]-2(1+1.22)=4.8Δt+2(Δt)2,
故物体在1.2 s末的瞬时速度为4.8 m/s.
①在极限表达式中,可把Δx作为一个数来参与运算.
②求出 的表达式后,Δx无限趋近于0,可令Δx=0,求出结果即可.
一做直线运动的物体,其位移s与时间t的关系是s(t)=3t-t2.
(1)求此物体的初速度;
(2)求此物体在t=2时的瞬时速度.
(1)t=0时的速度为初速度.在0时刻取一时间段[0,0+Δt],即[0,Δt],所以Δs=s(Δt)-s(0)=[3Δt-(Δt)2]-(3×0-02)
=3Δt-(Δt)2,
所以物体的初速度为3.
(2)取一时间段[2,2+Δt],所以Δs=s(2+Δt)-s(2)
=[3(2+Δt)-(2+Δt)2]-(3×2-22)=-Δt-(Δt)2,
( )
抛物线的切线的斜率
当点P无限趋近于P0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为抛物线f(x)在点P0处的切线,我们可以用割线P0P的斜率k近似地表示切线P0T的斜率k0.
x
y
o
P0
P
例3 求抛物线y=2x2+4x在点(3,30)处的切线方程.
Δy=2(3+Δx)2+4(3+Δx)-(2×32+4×3)
=12Δx+2(Δx)2+4Δx=2(Δx)2+16Δx
∴在点(3,30)处的切线方程为:y-30=16(x-3)即:16x-y-18=0.
求抛物线y=x2+3在点(2,7)处的切线方程.
Δy=[(2+Δx)2+3]-(22+3)=4Δx+(Δx)2
∴在点(2,7)处的切线方程为:y-7=4(x-2)
即:4x-y-1=0.
课时总结
1.平均速度只能粗略地反映物体在一段时间内里的运动状态,并不代表物体在每时每刻的运动情况,但是它是求瞬时速度的基础,瞬时速度是平均速度当Δt→0时的极限值.
2.函数y=f (x)在x=x0处的切线斜率反映了函数在该点处的瞬时变化率,它揭示了事物在某时刻的变化情况.
