人教A版(2019)选择性必修第二册5.1.2导数的概念及几何意义 课件(共28张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册5.1.2导数的概念及几何意义 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 00:00:00 | ||
图片预览








文档简介
5.1.2导数的概念及
几何意义
新课程标准解读
核心素养
1.经历由平均变化率到瞬时变化率的过程,体会导数的概念的实际背景.
2.了解导函数的概念,理解导数的几何意义.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
1.通过导数概念和导数几何意义的学习,培养学生数学抽象及直观想象的核心素养.
2.借助切线方程的求解,提升学生的数学运算核心素养.
情境导入
下雨天,当我们将雨伞转动时,伞面边沿的水滴沿着伞的切线方向飞出.实际上物体(看作质点)做曲线运动时,运动方向在不停地变化,其速度方向为质点在其轨迹曲线上的切线方向,我们可以利用导数研究曲线的切线问题.
水滴沿伞边切线飞出
2019年国际田联钻石联赛伦敦站男子200米比赛,中国选手谢震业以19秒88夺冠,这不仅刷新了全国纪录,还创造了新的亚洲纪录.赛后各国教练都在研究他的弯道技术,通过回放录像分析其弯道时的运动方向.这需要求运动曲线在任一点的切线.怎样求曲线的切线?
一、导数的概念
1.函数的平均变化率
对于函数y=f(x),设自变量x从x0变化到x0+Δx,相应地,函数值y就从f(x0)变化到f(x0+Δx),这时,x的变化量为Δx,y的变化量为Δy=f(x0+Δx)-f(x0).我们把比值 ,即 =______________________叫做函数y=f(x)从x0到x0+Δx的平均变化率.
?y
?x
?y
?x
2.函数在x=x0处的导数
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
?y
?x
?y
?x
对导数概念的再理解
(1)函数应在点x0的附近有定义,否则导数不存在;
(2)导数是一个局部概念,它只与函数y=f(x)在x=x0及其附近的函数值有关,与Δx无关;
(3)导数的实质是一个极限值.
1.已知f(x)=2x+1,则f′(1)=________.
解析:
lim
?x→0
4x
f(x0+x)-f(x0+x-4x)
=4
二、导数的几何意义
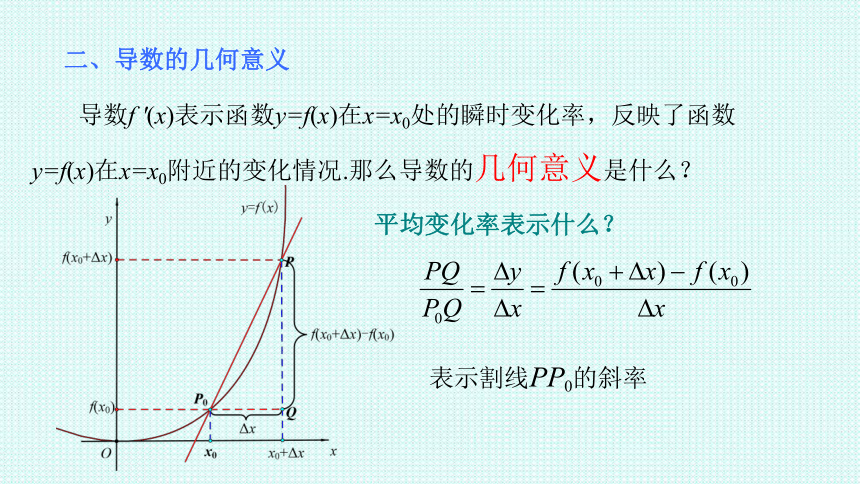
导数f '(x)表示函数y=f(x)在x=x0处的瞬时变化率,反映了函数y=f(x)在x=x0附近的变化情况.那么导数的几何意义是什么?
平均变化率表示什么?
表示割线PP0的斜率
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
割线P0P 的斜率
当 时,k 无限接近函数
y=f(x)在x=x0的导数f '(x0)
导数的几何意义:f '(x)是函数 y=f(x) 在x=x0处切线P0T的斜率.
(1)曲线的切线与割线
①曲线的切线是由割线绕一点转动,当另一点无限接近这一点时割线趋于的直线.
②曲线的切线就是割线趋近于某一确定位置的直线,体现了无限趋近的思想.
(2)曲线的切线与导数
①函数f(x)在x=x0处有导数,则在该点处函数f(x)表示的曲线必有切线,且导数值是该切线的斜率.
②函数f(x)表示的曲线在点(x0,f(x0))处有切线,但函数f(x)在该点处不一定可导,如f(x)= 在x=0处有切线,但不可导.
曲线的切线并不一定与曲线只有一个交点,可以有多个,甚至可以有无穷多个.与曲线只有一个公共点的直线也不一定是曲线的切线.
3
三、导函数
对于函数y=f(x),当x=x0时,f′(x0)是一个确定的数,当x变化时,f′(x)便是一个关于x的函数,我们称它为函数y=f(x)的导函数(简称为导数),即f′(x)=y′=________________.
题型一
求函数在某点处的导数
简称:一差、二比、三极限
设曲线y=x2+x-2在点M处的切线斜率为3,则点M的坐标为( )
A.(0,-2) B.(1,0) C.(0,0) D.(1,1)
设点M(x0,y0),
∴k=
=2x0+1,
令2x0+1=3,∴x0=1,则y0=0.
题型二
求曲线的切线方程
[例2] (链接教科书第70页练习2题)已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点(1,1)的切线方程.
(1)将x=1代入曲线C的方程得y=1,∴切点P(1,1).
∴k=y′|x=1=3.
∴曲线在点P(1,1)处的切线方程为y-1=3(x-1),
即3x-y-2=0.
(2)设切点为Q(x0,y0),由(1)可知y′|x=x0=3x02,由题意可知kPQ=y′|x=x0,
①当x0=1时,切点坐标为(1,1),相应的切线方程为3x-y-2=0.
相应的切线方程为3x-4y+1=0.
求曲线y=x2+1过点P(1,0)的切线方程.
设切点为Q(a,a2+1),
∵在点Q处的切线方程为y-(a2+1)=2a(x-a),*
把点(1,0)代入(*)式得-(a2+1)=2a(1-a).
题型三
导数几何意义的应用
探究1 求切点坐标
例3 已知曲线y=x2+6的切线分别符合下列条件,求切点.
(1)平行于直线y=4x-3;
(2)垂直于直线2x-y+5=0.
设切点坐标为(x0,y0).f′(x)=
∴过(x0,y0)的切线的斜率为2x0.
(1)∵切线与直线y=4x-3平行,∴2x0=4,x0=2,y0=x02+6=10,
即过曲线y=x2+6上点(2,10)的切线与直线y=4x-3平行.
(2)∵切线与直线2x-y+5=0垂直,
∴2x0×2=-1,
即过曲线y=x2+6上点
的切线与直线2x-y+5=0垂直.
探究2 与曲线的切点相关的问题
例4 已知直线l1为曲线y=x2+x-2在(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴围成的三角形面积.
(1)y′=
所以y′|x=1=2×1+1=3,
所以直线l1的方程为y=3(x-1),即y=3x-3.
设直线l2过曲线y=x2+x-2上的点B(b,b2+b-2),
则l2的方程为y=(2b+1)x-b2-2.因为l1⊥l2,
1.如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
o
x
y
P
5
点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且f′(5)=-1,∴f(5)+f′(5)=2.
2.已知函数y=f(x)的图象如图,则f′(xA)与f′(xB)的大小关系是( )
A.0>f′(xA)>f′(xB) B.f′(xA)C.f′(xA)=f′(xB) D.f′(xA)>f′(xB)>0
o
x
y
B
A
3.李华在参加一次同学聚会时,用如图所示的圆口杯喝饮料,他想:如果向杯子中倒饮料的速度一定(即单位时间内倒入的饮料量相同),那么杯子中饮料的高度h是关于时间t的函数h(t),则函数h(t)的图象可能是 ( )
o
t
h
o
t
h
o
t
h
o
t
h
h0
h0
h0
h0
t0
t0
t0
t0
由于圆口杯是“下细上粗”,则开始饮料高度增加较快,以后饮料高度增加得越来越慢,仅有B符合.
A
B
C
D
1.导数的定义
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
?y
?x
?y
?x
2.导数的几何意义
曲线y=f(x)在点(x0,y0)的切线斜率为.
几何意义
新课程标准解读
核心素养
1.经历由平均变化率到瞬时变化率的过程,体会导数的概念的实际背景.
2.了解导函数的概念,理解导数的几何意义.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
1.通过导数概念和导数几何意义的学习,培养学生数学抽象及直观想象的核心素养.
2.借助切线方程的求解,提升学生的数学运算核心素养.
情境导入
下雨天,当我们将雨伞转动时,伞面边沿的水滴沿着伞的切线方向飞出.实际上物体(看作质点)做曲线运动时,运动方向在不停地变化,其速度方向为质点在其轨迹曲线上的切线方向,我们可以利用导数研究曲线的切线问题.
水滴沿伞边切线飞出
2019年国际田联钻石联赛伦敦站男子200米比赛,中国选手谢震业以19秒88夺冠,这不仅刷新了全国纪录,还创造了新的亚洲纪录.赛后各国教练都在研究他的弯道技术,通过回放录像分析其弯道时的运动方向.这需要求运动曲线在任一点的切线.怎样求曲线的切线?
一、导数的概念
1.函数的平均变化率
对于函数y=f(x),设自变量x从x0变化到x0+Δx,相应地,函数值y就从f(x0)变化到f(x0+Δx),这时,x的变化量为Δx,y的变化量为Δy=f(x0+Δx)-f(x0).我们把比值 ,即 =______________________叫做函数y=f(x)从x0到x0+Δx的平均变化率.
?y
?x
?y
?x
2.函数在x=x0处的导数
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
?y
?x
?y
?x
对导数概念的再理解
(1)函数应在点x0的附近有定义,否则导数不存在;
(2)导数是一个局部概念,它只与函数y=f(x)在x=x0及其附近的函数值有关,与Δx无关;
(3)导数的实质是一个极限值.
1.已知f(x)=2x+1,则f′(1)=________.
解析:
lim
?x→0
4x
f(x0+x)-f(x0+x-4x)
=4
二、导数的几何意义
导数f '(x)表示函数y=f(x)在x=x0处的瞬时变化率,反映了函数y=f(x)在x=x0附近的变化情况.那么导数的几何意义是什么?
平均变化率表示什么?
表示割线PP0的斜率
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
割线P0P 的斜率
当 时,k 无限接近函数
y=f(x)在x=x0的导数f '(x0)
导数的几何意义:f '(x)是函数 y=f(x) 在x=x0处切线P0T的斜率.
(1)曲线的切线与割线
①曲线的切线是由割线绕一点转动,当另一点无限接近这一点时割线趋于的直线.
②曲线的切线就是割线趋近于某一确定位置的直线,体现了无限趋近的思想.
(2)曲线的切线与导数
①函数f(x)在x=x0处有导数,则在该点处函数f(x)表示的曲线必有切线,且导数值是该切线的斜率.
②函数f(x)表示的曲线在点(x0,f(x0))处有切线,但函数f(x)在该点处不一定可导,如f(x)= 在x=0处有切线,但不可导.
曲线的切线并不一定与曲线只有一个交点,可以有多个,甚至可以有无穷多个.与曲线只有一个公共点的直线也不一定是曲线的切线.
3
三、导函数
对于函数y=f(x),当x=x0时,f′(x0)是一个确定的数,当x变化时,f′(x)便是一个关于x的函数,我们称它为函数y=f(x)的导函数(简称为导数),即f′(x)=y′=________________.
题型一
求函数在某点处的导数
简称:一差、二比、三极限
设曲线y=x2+x-2在点M处的切线斜率为3,则点M的坐标为( )
A.(0,-2) B.(1,0) C.(0,0) D.(1,1)
设点M(x0,y0),
∴k=
=2x0+1,
令2x0+1=3,∴x0=1,则y0=0.
题型二
求曲线的切线方程
[例2] (链接教科书第70页练习2题)已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点(1,1)的切线方程.
(1)将x=1代入曲线C的方程得y=1,∴切点P(1,1).
∴k=y′|x=1=3.
∴曲线在点P(1,1)处的切线方程为y-1=3(x-1),
即3x-y-2=0.
(2)设切点为Q(x0,y0),由(1)可知y′|x=x0=3x02,由题意可知kPQ=y′|x=x0,
①当x0=1时,切点坐标为(1,1),相应的切线方程为3x-y-2=0.
相应的切线方程为3x-4y+1=0.
求曲线y=x2+1过点P(1,0)的切线方程.
设切点为Q(a,a2+1),
∵在点Q处的切线方程为y-(a2+1)=2a(x-a),*
把点(1,0)代入(*)式得-(a2+1)=2a(1-a).
题型三
导数几何意义的应用
探究1 求切点坐标
例3 已知曲线y=x2+6的切线分别符合下列条件,求切点.
(1)平行于直线y=4x-3;
(2)垂直于直线2x-y+5=0.
设切点坐标为(x0,y0).f′(x)=
∴过(x0,y0)的切线的斜率为2x0.
(1)∵切线与直线y=4x-3平行,∴2x0=4,x0=2,y0=x02+6=10,
即过曲线y=x2+6上点(2,10)的切线与直线y=4x-3平行.
(2)∵切线与直线2x-y+5=0垂直,
∴2x0×2=-1,
即过曲线y=x2+6上点
的切线与直线2x-y+5=0垂直.
探究2 与曲线的切点相关的问题
例4 已知直线l1为曲线y=x2+x-2在(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴围成的三角形面积.
(1)y′=
所以y′|x=1=2×1+1=3,
所以直线l1的方程为y=3(x-1),即y=3x-3.
设直线l2过曲线y=x2+x-2上的点B(b,b2+b-2),
则l2的方程为y=(2b+1)x-b2-2.因为l1⊥l2,
1.如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
o
x
y
P
5
点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且f′(5)=-1,∴f(5)+f′(5)=2.
2.已知函数y=f(x)的图象如图,则f′(xA)与f′(xB)的大小关系是( )
A.0>f′(xA)>f′(xB) B.f′(xA)
o
x
y
B
A
3.李华在参加一次同学聚会时,用如图所示的圆口杯喝饮料,他想:如果向杯子中倒饮料的速度一定(即单位时间内倒入的饮料量相同),那么杯子中饮料的高度h是关于时间t的函数h(t),则函数h(t)的图象可能是 ( )
o
t
h
o
t
h
o
t
h
o
t
h
h0
h0
h0
h0
t0
t0
t0
t0
由于圆口杯是“下细上粗”,则开始饮料高度增加较快,以后饮料高度增加得越来越慢,仅有B符合.
A
B
C
D
1.导数的定义
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
?y
?x
?y
?x
2.导数的几何意义
曲线y=f(x)在点(x0,y0)的切线斜率为.
