人教A版(2019)选择性必修第二册5.2.1基本初等函数的导数 课件(共18张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册5.2.1基本初等函数的导数 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-06 20:50:52 | ||
图片预览





文档简介
(共18张PPT)
5.2.1 基本初等函数的导数
新课程标准解读 核心素养
1.通过对六个简单的常用函数的求导,体会导数求解的一般方法以及特殊到一般的思想. 2.掌握基本初等函数的导数公式. 1.数学运算:求简单函数的导数.
2.直观想象:利用导数求曲线的切线.
情境导入
根据导数的定义,求函数 y=f(x) 的导数的三个步骤:
2.算比值:
1.求增量:
3.取极限:
求导数不能每次都求极限,有没有更直接出结果的方法?
如何利用定义求出 y=c ,y=x,y=x2, 的导数?
课堂探究
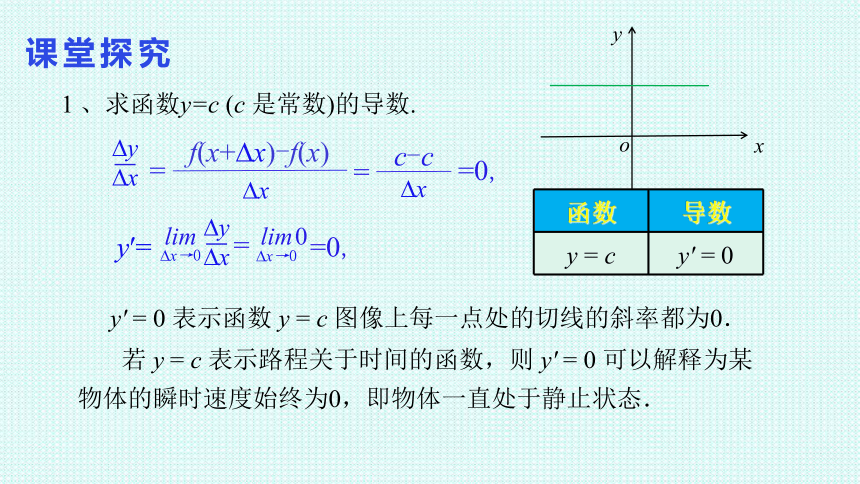
1 、求函数y=c (c 是常数)的导数.
y
x
=
f(x+ x)-f(x)
x
=
c-c
x
=0,
y′=
lim
x→0
y
x
=0,
=
lim
x→0
0
y' = 0 表示函数 y = c 图像上每一点处的切线的斜率都为0.
若 y = c 表示路程关于时间的函数,则 y' = 0 可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态.
o
x
y
函数 导数
y = c y' = 0
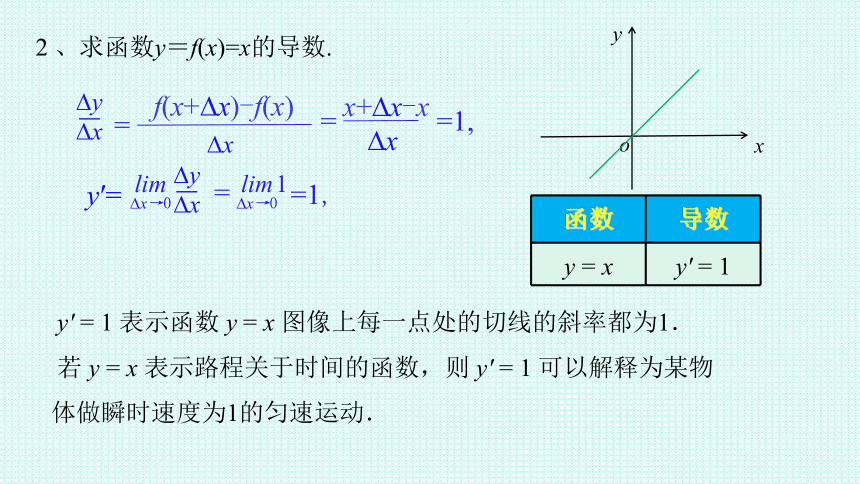
2 、求函数y=f(x)=x的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x-x
=1,
y′=
lim
x→0
y
x
=1,
=
lim
x→0
1
o
x
y
函数 导数
y = x y' = 1
y' = 1 表示函数 y = x 图像上每一点处的切线的斜率都为1.
若 y = x 表示路程关于时间的函数,则 y' = 1 可以解释为某物体做瞬时速度为1的匀速运动.
3、求函数y=f(x)=x2的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)2-x2
=2x+ x,
y′=
lim
x→0
y
x
=2x,
=
lim
x→0
(2x+ x)
函数 导数
y = x2 y' = 2x
o
x
y
y' = 2x 表示函数 y = x2 图像上点(x, y)处的切线的斜率都为2x,说明随着 x 的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看,表明:当 x<0时,随着 x 的增加,函数 y = x2 减少得越来越慢;当x>0时,随着 x 的增加,函数 y = x2 增加得越来越快.
4、求函数y=f(x)=x3的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)3-x3
=3x2+3x· x+( x)2,
o
x
y
y′=
lim
x→0
y
x
=3x2,
=
lim
x→0
(3x2+3x· x+( x)2)
函数 导数
y = x3 y' = 3x2
y'=3x2表示函数y=x3的图象上点(x,y)处切线的斜率为3x2,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
5、求函数y=f(x)= 的导数.
1
x
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x
1
x
1
-
-
x2+x· x
1
=
y′=
lim
x→0
y
x
-
x2+x· x
1
( )
= ,
=
lim
x→0
1
x2
-
函数 导数
y = y' =-
1
x
1
x2
基本初等函数的导数公式
原函数 导函数
(1)f(x)=c f′(x)=0
(2)f(x)=xn(n∈Q) f′(x)=n·xn-1
(3)f(x)=sinx f′(x)=cosx
(4)f(x)=cosx f′(x)=-sinx
(5)f(x)=ax f′(x)=axlna
(6)f(x)=ex f′(x)=ex
(7)f(x)=logax f′(x)=
(8)f(x)=lnx f′(x)=
题型一 利用导数公式求函数的导数
例1 求下列函数的导数:
(1)y=sin ;(2)y=5x;(3)y= ;(4)y= ;(5)y=log3x.
π
3
1
x4
(1)y'=0
(2)y'=(5x)′=5xln 5
(5)y′=(log3x)′
= ,
1
xln3
(4)y′=(x )′
3
5
3
5
x
-
2
5
=
已知 f (x) = cosx,g (x) = x,求适合 f ' (x)+g'(x) = 0 的 x 的值
f ' (x)=-sinx,g'(x)=1,
f ' (x)+g'(x) = 0即sinx=1.
表面终边落在y的正半轴
{x|x= +2kπ,k∈Z}
π
2
f′(1)=1,
所以ln a=1,所以a=e.
题型二 利用导数公式求切线方程
因为切线与y=2x-4平行,
即16x-8y+1=0.
已知函数 y=x3-3x,过点 A (0,16) 作曲线 y=f (x) 的切线,求此
切线方程.
解:点 A (0, 16) 不在曲线上.设切点为 M (x0, y0) ,则有 y0 = x03- 3x0 .
因 f '(x0)=3(x02-1),故切线的方程为 y-y0 =3(x02-1)(x-x0) .
点A (0, 16)在切线上,则有16-(x03- 3x0) =3(x02-1)(0-x0) .
化简得 x03 =-8,解得 x0 =-2.
所以,切点为M (-2, -2),切线方程为 9x-y+16=0.
过点要设切点,切点满足已知函数解析式,切点满足切线方程。
设切点为(x0,lnx0),
因为曲线y=ln x在x=x0处的切线为x-y+c=0,其斜率为1.
y′|x=x0= =1,
1
x0
x0=1,
所以切点为(1,0).
所以1-0+c=0,所以c=-1.
题型三 导数的综合应用
例3(链接教科书第75页例2)(1)质点的运动方程是S(t)=sin t,则质点在t= 时的速度为________;质点运动的加速度为________;
(2)已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.
(1) v(t)=S′(t)=cos t,
∵v(t)=cos t,
∴加速度a(t)=v′(t)=(cos t)′=-sin t.
(2)由于y=sin x,y=cos x,设这两条曲线的一个公共点为P(x0,y0).∴两条曲线在P(x0,y0)处的斜率分别为k1=cos x0,k2=-sin x0.
若使两条切线互相垂直,必须cos x0·(-sin x0)=-1,
即sin x0·cos x0=1,也就是sin 2x0=2,这是不可能的.
∴两条曲线不存在公共点,使在这一点处的两条切线互相垂直.
由y=ex得y′=ex,曲线在点(0,1)处的斜率k1=e0=1,
设P(m,n),
由题意知k1k2=-1,所以k2=-1,由此易得m=1,n=1,
即点P的坐标为(1,1),k2=-1.所以点P处的切线方程为x+y-2=0.
设曲线 y=xn+1(n∈N*) 在点(1, 1)处的切线与 x 轴的交点的横坐标为xn,令an=lg xn,则 a1+a2+…+a99 的值为________.
∵y=xn+1,∴y′=(n+1)xn,y′ | x=1=n+1.
∴曲线在点(1, 1)处的切线方程为 y-1=(n+1)(x-1).
令y=0,
xn=
n+1
n
故an=lg n-lg (n+1).
∴a1 + a2 +…+ a99=(lg 1-lg 2)+(lg 2-lg 3)+…+(lg 98-lg 99)+(lg 99-lg 100)=lg 1-lg 100=-2.
1.应用导数的定义求导,是求导数的基本方法,但运算较繁琐,而利用导数公式求导数,可以简化求导过程,降低运算难度,是常用的求导方法.
2.利用导数公式求导,应根据所给问题的特征,恰当地选择求导公式.有时还要先对函数解析式进行化简整理,这样能够简化运算过程.
5.2.1 基本初等函数的导数
新课程标准解读 核心素养
1.通过对六个简单的常用函数的求导,体会导数求解的一般方法以及特殊到一般的思想. 2.掌握基本初等函数的导数公式. 1.数学运算:求简单函数的导数.
2.直观想象:利用导数求曲线的切线.
情境导入
根据导数的定义,求函数 y=f(x) 的导数的三个步骤:
2.算比值:
1.求增量:
3.取极限:
求导数不能每次都求极限,有没有更直接出结果的方法?
如何利用定义求出 y=c ,y=x,y=x2, 的导数?
课堂探究
1 、求函数y=c (c 是常数)的导数.
y
x
=
f(x+ x)-f(x)
x
=
c-c
x
=0,
y′=
lim
x→0
y
x
=0,
=
lim
x→0
0
y' = 0 表示函数 y = c 图像上每一点处的切线的斜率都为0.
若 y = c 表示路程关于时间的函数,则 y' = 0 可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态.
o
x
y
函数 导数
y = c y' = 0
2 、求函数y=f(x)=x的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x-x
=1,
y′=
lim
x→0
y
x
=1,
=
lim
x→0
1
o
x
y
函数 导数
y = x y' = 1
y' = 1 表示函数 y = x 图像上每一点处的切线的斜率都为1.
若 y = x 表示路程关于时间的函数,则 y' = 1 可以解释为某物体做瞬时速度为1的匀速运动.
3、求函数y=f(x)=x2的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)2-x2
=2x+ x,
y′=
lim
x→0
y
x
=2x,
=
lim
x→0
(2x+ x)
函数 导数
y = x2 y' = 2x
o
x
y
y' = 2x 表示函数 y = x2 图像上点(x, y)处的切线的斜率都为2x,说明随着 x 的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看,表明:当 x<0时,随着 x 的增加,函数 y = x2 减少得越来越慢;当x>0时,随着 x 的增加,函数 y = x2 增加得越来越快.
4、求函数y=f(x)=x3的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)3-x3
=3x2+3x· x+( x)2,
o
x
y
y′=
lim
x→0
y
x
=3x2,
=
lim
x→0
(3x2+3x· x+( x)2)
函数 导数
y = x3 y' = 3x2
y'=3x2表示函数y=x3的图象上点(x,y)处切线的斜率为3x2,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
5、求函数y=f(x)= 的导数.
1
x
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x
1
x
1
-
-
x2+x· x
1
=
y′=
lim
x→0
y
x
-
x2+x· x
1
( )
= ,
=
lim
x→0
1
x2
-
函数 导数
y = y' =-
1
x
1
x2
基本初等函数的导数公式
原函数 导函数
(1)f(x)=c f′(x)=0
(2)f(x)=xn(n∈Q) f′(x)=n·xn-1
(3)f(x)=sinx f′(x)=cosx
(4)f(x)=cosx f′(x)=-sinx
(5)f(x)=ax f′(x)=axlna
(6)f(x)=ex f′(x)=ex
(7)f(x)=logax f′(x)=
(8)f(x)=lnx f′(x)=
题型一 利用导数公式求函数的导数
例1 求下列函数的导数:
(1)y=sin ;(2)y=5x;(3)y= ;(4)y= ;(5)y=log3x.
π
3
1
x4
(1)y'=0
(2)y'=(5x)′=5xln 5
(5)y′=(log3x)′
= ,
1
xln3
(4)y′=(x )′
3
5
3
5
x
-
2
5
=
已知 f (x) = cosx,g (x) = x,求适合 f ' (x)+g'(x) = 0 的 x 的值
f ' (x)=-sinx,g'(x)=1,
f ' (x)+g'(x) = 0即sinx=1.
表面终边落在y的正半轴
{x|x= +2kπ,k∈Z}
π
2
f′(1)=1,
所以ln a=1,所以a=e.
题型二 利用导数公式求切线方程
因为切线与y=2x-4平行,
即16x-8y+1=0.
已知函数 y=x3-3x,过点 A (0,16) 作曲线 y=f (x) 的切线,求此
切线方程.
解:点 A (0, 16) 不在曲线上.设切点为 M (x0, y0) ,则有 y0 = x03- 3x0 .
因 f '(x0)=3(x02-1),故切线的方程为 y-y0 =3(x02-1)(x-x0) .
点A (0, 16)在切线上,则有16-(x03- 3x0) =3(x02-1)(0-x0) .
化简得 x03 =-8,解得 x0 =-2.
所以,切点为M (-2, -2),切线方程为 9x-y+16=0.
过点要设切点,切点满足已知函数解析式,切点满足切线方程。
设切点为(x0,lnx0),
因为曲线y=ln x在x=x0处的切线为x-y+c=0,其斜率为1.
y′|x=x0= =1,
1
x0
x0=1,
所以切点为(1,0).
所以1-0+c=0,所以c=-1.
题型三 导数的综合应用
例3(链接教科书第75页例2)(1)质点的运动方程是S(t)=sin t,则质点在t= 时的速度为________;质点运动的加速度为________;
(2)已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.
(1) v(t)=S′(t)=cos t,
∵v(t)=cos t,
∴加速度a(t)=v′(t)=(cos t)′=-sin t.
(2)由于y=sin x,y=cos x,设这两条曲线的一个公共点为P(x0,y0).∴两条曲线在P(x0,y0)处的斜率分别为k1=cos x0,k2=-sin x0.
若使两条切线互相垂直,必须cos x0·(-sin x0)=-1,
即sin x0·cos x0=1,也就是sin 2x0=2,这是不可能的.
∴两条曲线不存在公共点,使在这一点处的两条切线互相垂直.
由y=ex得y′=ex,曲线在点(0,1)处的斜率k1=e0=1,
设P(m,n),
由题意知k1k2=-1,所以k2=-1,由此易得m=1,n=1,
即点P的坐标为(1,1),k2=-1.所以点P处的切线方程为x+y-2=0.
设曲线 y=xn+1(n∈N*) 在点(1, 1)处的切线与 x 轴的交点的横坐标为xn,令an=lg xn,则 a1+a2+…+a99 的值为________.
∵y=xn+1,∴y′=(n+1)xn,y′ | x=1=n+1.
∴曲线在点(1, 1)处的切线方程为 y-1=(n+1)(x-1).
令y=0,
xn=
n+1
n
故an=lg n-lg (n+1).
∴a1 + a2 +…+ a99=(lg 1-lg 2)+(lg 2-lg 3)+…+(lg 98-lg 99)+(lg 99-lg 100)=lg 1-lg 100=-2.
1.应用导数的定义求导,是求导数的基本方法,但运算较繁琐,而利用导数公式求导数,可以简化求导过程,降低运算难度,是常用的求导方法.
2.利用导数公式求导,应根据所给问题的特征,恰当地选择求导公式.有时还要先对函数解析式进行化简整理,这样能够简化运算过程.
